Автореферат:

Вступ

Коливальний рух частинок пружного середовища, що розповсюджується у вигляді хвиль - можна представити у вигляді спектра послідовних значень гучності для тонів різної висоти.

Подібні перетворення можна виконувати за допомогою математичних методів практично над будь-якими коливальними процесами - від світлових хвиль і океанських припливів до циклів сонячної активності. Користуючись цими математичними прийомами, можна розкладати функції, представляючи коливальні процеси у вигляді набору синусоїдальних складових - хвилеподібних кривих, що переходять від максимуму до мінімуму, а потім знову до максимуму, подібно до океанської хвилі. Перетворення Фур'є - це функція, що описує амплітуду та фазу кожної синусоїда, що відповідає певній частоті. Амплітуда представляє висоту кривої, а фаза - початкову точку синусоїда.

Математичні основи перетворення Фур'є

Незалежно від способу, яким виходить перетворення, для кожної частоти необхідно вказати два числа. Це можуть бути амплітуда і частота, однак ту ж інформацію можуть кодувати та інші пари чисел. Ці значення можна виразити у вигляді одного комплексного числа. (Комплексне число представляє собою суму одного дійсного числа з іншим дійсним числом, помноженим на квадратний корінь мінус одиниці.) Таким поданням користуються дуже широко, так як воно дозволяє залучити математичний апарат алгебри комплексних чисел. Теорія функцій комплексних змінних і перетворення Фур'є стали необхідними в чисельних розрахунках, що проводяться при конструюванні електричних ланцюгів, аналізі механічних коливань та вивченні механізму розповсюдження хвиль.

Послідовність N комплексних чисел x0, ..., xN - 1 перетворюється в послідовність з N комплексних чисел X0, ..., XN - 1 за допомогою дискретного перетворення Фур'є за формулою [6]:

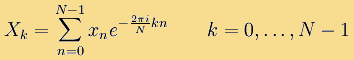
де i - це мнима одиниця. Зворотне дискретне перетворення Фур'є задається формулою

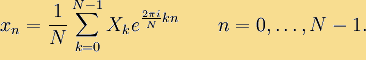
Актуальність проблеми та сфери застосування

Існують три основні області застосування таких перетворень для обробки зображень. По-перше, перетворення використовуються для виділення характерних ознак зображення. Так, наприклад, постійна складова спектра Фур'є пропорційна середньої яскравості зображення, а високочастотні складові характеризують величину і орієнтацію його контурів. Іншою областю застосування перетворень є кодування зображень, коли ширина спектра зменшується за рахунок відкидання або грубого квантування малих за величиною коефіцієнтів перетворення. Третя область - це скорочення розмірності при виконанні обчислень. Інакше кажучи, в процесі обробки (наприклад, фільтрації) малі коефіцієнти перетворення можна відкинути без помітного погіршення якості обробки.

Процедура фільтрації зображення, заснована на перетворенні Фур'є, містить наступні кроки [2]:

Перевагою Фур'є фільтрації є можливість у реальному масштабі часу аналізувати спектр сигналу, на базі цього аналізу гнучко підбирати параметри фільтра та спостерігати результат фільтрації з наступною корекцією параметрів фільтра, якщо в цьому є необхідність.

В процесі виконання даної роботи планується одержати результати по ефективності паралельної реалізації ШПФ для цифрових зображень. Будуть розраховані часові витрати і витрати обчислювальних ресурсів. Також планується виділити класи зображень, для яких будуть максимально ефективними ті чи інші перетворення.

Найбільш ефективне перетворення Фур'є розмірністю, що є ступенем двійки. В реальних задачах часто розмірність ШПФ такої не є. Тоді задачу зводять до такої, але це не завжди зручно. Існують алгоритми, що дозволяють вирішувати цю задачу, не вдаючись до її збільшення [3].

Заплановані результати та наукова новизна роботи

У результаті планується застосовувати до зображень саме ті алгоритми, які будуть максимально ефективні для даного класу зображень.
Керівником були поставлені такі завдання.

Висновки

Завдяки універсальності підходу, у цього методу найширший спектр застосування, в тому числі і для обробки цифрових зображень.

В подальшому при виконанні магістерської роботи буде розроблена програмна система для виконанню швидкого перетворення Фур'є паралельним блочний методом. І на підставі даних, отриманих за допомогою цієї системи, буде можливим оцінити показники ефективності паралельного рішення ШПФ для зображень різного виду.

Список використаної літератури

1. Ronald N. Bracewell. The Fourier Transform and its Applications (second edition, revised). McGraw-Hill Book Company, 1986.

2. Прэтт У. Цифровая обработка изображений: Пер. с англ.—М.: Мир, 1982.— Кн.1—312 с.

3. Гонсалес Р. Вудс Р. Цифровая обработка изображений Москва: Техносфера, 2005. – 1072 с.

4. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов Москва «Мир» 1989.—448 с

5. www.fftw.org Офіційний сайт спільноти фахівців, що займаються проблемою паралельної реалізації алгоритмів швидкого перетворення Фур'є

6. www.wikipedia.org Опис дискретного перетворення Фур'є у вільній енциклопедіі "Вікіпедія"

7. Рональда Н. Брейсуэлл. Журнал Scientific American (Издание на русском языке) № 8 · АВГУСТ 1989 · С. 48–56.

8. Воеводин В.В.,"Вычислительная математика и структура алгоритмов.".-М.: Изд-во МГУ, 2006.-112 с.

9. Говидараю Н.К., Ллойд Б., Доценко Ю., Смит Б., Манферделли Д. Высокопроизводительные дискретные преобразования Фурье на графических процессорах

10. Потопальский В.В. Оценка качества преобразования Фурье в радиотехнических и телевизионных системах. Львов, 1993. 189 с.

11. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. Москва, Мир – 1989. —448 с.