Abstract:

Introduction

The Discrete Fourier Transform (DFT) is a specific form of Fourier analysis to convert one function into another (frequency domain). DFT is widely employed in signal processing and related fields to analyze frequencies contained in a sample signal, to solve partial differential equations, and to perform other operations such as convolutions. Fast Fourier Transform (FFT) is an efficient implementation of DFT and is used, apart from other fields, in digital image processing. Fast Fourier Transform is applied to convert an image from the image (spatial) domain to the frequency domain. Applying filters to images in frequency domain is computationally faster than to do the same in the image domain.

Mathematical foundations of Fast Fourier Transform

Fourier Transform decomposes an image into its real and imaginary components which is a representation of the image in the frequency domain. If the input signal is an image then the number of frequencies in the frequency domain is equal to the number of pixels in the image or spatial domain. The inverse transform re-transforms the frequencies to the image in the spatial domain. The FFT and its inverse of a 2D image are given by the following equations:

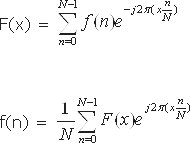
Where f(m,n) is the pixel at coordinates (m, n), F(x,y) is the value of the image in the frequency domain corresponding to the coordinates x and y, M and N are the dimensions of the image.

As can be seen from the equation, a native implementation of this algorithm is very expensive. But the beauty of FFT is that it is separable, namely, the 2D transform can be done as 2 1D transforms as shown below (shown only in the horizontal direction) - one in the horizontal direction followed by the other in the vertical direction on the result of the horizontal transform. The end result is equivalent to performing the 2D transform in the frequency space.

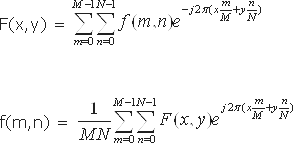
The FFT that's implemented in the application here requires that the dimensions of the image are a power of two. Another interesting property of the FFT is that the transform of N points can be rewritten as the sum of two N/2 transforms (divide and conquer). This is important because some of the computations can be reused thus eliminating expensive operations.

The output of the Fourier Transform is a complex number and has a much greater range than the image in the spatial domain. Therefore to accurately represent these values, they are stored as floats. Furthermore, the dynamic range of the Fourier coefficients are too large to be displayed on the screen, and hence, these values are scaled (usually by dividing by Height*Width of the image) to bring them within the range of values that can be displayed [12].

Actuality of the subject

There are three main areas of application of such transformations for image processing. First, the transformation is used to highlight the salient features of the image. For example, the constant component of the Fourier spectrum is proportional to the average brightness, and high-frequency components characterize the size and orientation of its contours. Another area of application is to change the coding of images when the width of the spectrum is reduced at the expense of coarse quantization, or reject the small size of the coefficients of transformation. The third area - this is a reduction of dimension in the performance calculations. In other words, in the process of processing (eg, filtering), the small conversion factors can be discarded without a noticeable deterioration in the quality of processing.

The procedure for filtering images based on Fourier transform, the following steps[2]:

The advantage of Fourier filtering is the possibility of real-time analysis of the spectrum signal based on this analysis, flexibility to choose options to filter and observe the result of filtering with subsequent correction of parameters of the filter, if necessary.

In carrying out this work is scheduled to receive the results on the effectiveness of the parallel implementation of FFT for digital images. Will be calculated the time spent and the cost of computing resources. Also it is planned to allocate classes of images, which will be most effective the various transformations.

The most efficient Fourier transform dimension is the degree of deuces. In real problems are often the dimension of DFT is not. Then the problem reduces to one, but it is not always convenient. There are algorithms to solve this problem without resorting to its increase [3].

Expected results and scientific novelty

As a result, plans to apply to the images are precisely the algorithms that will be most effective for this class of images.
The wokr lieader was placed such tasks:

Conclusions

Due to the universality of this method it can be used for a wide field of tasks including digital images processing.

Later in the process of the master's work will be developed software system for fast Fourier transform with the using of parallel block method. And on the basis of data obtained with help of this system, be possible to evaluate the performance of parallel FFT solutions for various types of images.

References

1. Ronald N. Bracewell. The Fourier Transform and its Applications (second edition, revised). McGraw-Hill Book Company, 1986.

2. Prett U. Cifrovaya obrabotka izobrajeniy: Per. s angl.-M.: Mir, 1982.- Kn.1-312 s.

3. Gonsales R. Vuds R. Cifrovaya obrabotka izobrajeniy Moskva: Tehnosfera, 2005. - 1072 s

4. Bleyhut R. Bystrye algoritmy cifrovoy obrabotki signalov Moskva 1989.-448 s.

5. www.fftw.org Official site of community professionals, dealing with the problem of parallel implementation of FFT algorithms.

6. www.wikipedia.org Description of the discrete Fourier transform from "Wikipedia".

7. Ronal'da N. Breysuell. Jurnal Scientific American (Izdanie na russkom yazyke) № 8 · AVGUST 1989 · S. 48-56.

8. Voevodin V.V.,"Vychislitel'naya matematika i struktura algoritmov.".-M.: Izd-vo MGU, 2006.-112 s.

9. Govidarayu N.K., Lloyd B., Docenko Yu., Smit B., Manferdelli D. Vysokoproizvoditel'nye diskretnye preobrazovaniya Fur'e na graficheskih processorah.

10. Potopal'skiy V.V. Ocenka kachestva preobrazovaniya Fur'e v radiotehnicheskih i televizionnyh sistemah. L'vov, 1993. 189 s.

11. Bleyhut R. Bystrye algoritmy cifrovoy obrabotki signalov. Moskva, Mir - 1989. -448 s.