


 ДонНТУ |
Портал магистров ДонНТУ
ДонНТУ |
Портал магистров ДонНТУ

Повышение качества деталей машин всегда являлось важнейшей задачей машиностроения.
С точки зрения обеспечения качества поверхностного слоя, наиболее актуальной является задача обоснования окончательного метода обработки ответственных поверхностей деталей, определяющих эксплуатационные свойства изделия в целом. Одним из перспективных путей решения этой задачи является использование обработки материалов тонким точением.
Объектом исследования являются корпусные детали, в частности будет рассматриваться деталь из чугуна "Блок цилиндра", к поверхности отверстия которого предъявляются высокие требования.
Наибольшая эффективность применения тонкого точения возможна при правильном, оптимальном выборе режимов резания, схем обработки, геометрии и конструкции инструментов. Для решения этих задач необходимо установление связи между эксплуатационными свойствами и параметрами поверхностного слоя деталей.

Разработка рекомендаций по выбору оптимальных режимов резания, разработка математической модели для расчета параметров оптимальных условий обработки, необходимых для решения задач обеспечения качества обработки деталей из чугуна и определяют актуальность данной магистерской работы.
Цель работы - повысить производительность и качество обработки деталей машин за счет выбора рациональных условий использования современных инструментальных материалов.
Эффективным способом повышения качества и точности обработки деталей является применение инструментов из сверхтвердых материалов, проводя исследования по этой теме можно выделить множество работ.
Так например в книге [10] авторами рассмотрены физико-технические свойства разновидностей кубического нитрида бора (эльбор-Р, белбор-Р, гексанит-Р и др.), синтетических алмазов и керамики. Изложены основные сведения по технологии их производства и областям применения. Приведены примеры обработки типовых деталей инструментами, оснащенными этими материалами.
Сведения о технологических процессах обработки поликристаллических сверхтвердых материалов (ПСТМ) при изготовлении и восстановлении режущего инструмента изложены в справочнике [11] Н.В. Новиковым. Так же в этой работе приведены режимы резания при обработке различных труднообрабатываемых материалов.
В работах [6] и [7] А.Г. Сусловым изучены закономерности формирования поверхностного слоя обрабатываемых деталей и условия рационального применения инструментальных материалов.
Но несмотря на большое количество исследований в этом направлении, многие вопросы остаются достаточно актуальными.
Одним из резервов повышения эффективности современного машиностроительного производства является применение сверхтвердых инструментальных материалов (СТМ) при обработке деталей машин. При использовании инструментов, оснащенных СТМ весьма актуальны исследования по определению оптимальных режимов резания, обеспечивающих для заданных условий обработки и требований к качеству обработанных поверхностей минимальную себестоимость.
Одним из наиболее распространенных методов оптимизации в настоящее время является метод линейного программирования [1, 2, 3], позволяющий осуществлять одновременную оптимизацию скорости резания и подачи с учетом действующих при резании ограничений по критерию максимальной производительности. Обязательным условием использования этого метода является возможность линеаризации целевой функции и ограничений. Несмотря на простоту и наглядность, этот метод не позволяет решать задачи оптимизации режимов резания в случае нелинейной целевой функции, каковой является себестоимость обработки деталей.
Такого недостатка лишен метод геометрического программирования (МГП), нашедший широкое применение для поиска оптимальных проектных решений в различных областях инженерных исследований, но недостаточно распространенный в теории механообработки [2]. В связи с этим представляет интерес дальнейшее развитие МГП применительно к задачам оптимизации режимов резания при использовании инструментов из СТМ.
Целью данной работы является опредение оптимальных режимов резания, обеспечивающих минимальную себестоимость обработки при заданном уровне качества обработанной поверхности при тонком точении с использованием резцов, оснащенных эльбором – Р.
Основное требование МГП состоит в том, что все компоненты задачи оптимизации должны быть выражены количественно в виде обобщенных положительных полиномов, называемых позиномами, от управляемых параметров. Возможность использования МГП для оптимизации режимов резания обусловлена тем, что целевая функция и ограничения могут быть представлены в виде суммы компонентов, каждый из которых выражается степенной функцией:
 (1)
(1)При оптимизации режимов резания тонкого точения в качестве критерия оптимизации принимается переменная часть себестоимости обработки детали режущим инструментом за один проход, зависящая от режимов резания:
 (2)
(2)Целевая функция, выражающая зависимость переменной части себестоимости от режимов резания, с учетом известных соотношений основного времени обработки и стойкости инструмента с режимами, имеет вид
 (3)
(3)В настоящей работе решается задача двухпараметрической оптимизации, то есть задача определения оптимальных значений скорости резания и подачи при заданной глубине резания в условиях однопроходной обработки (t = Δ).
Тогда целевая функция может быть представлена следующим образом:
 (4)
(4)где

Для тонкого точения необходимо учитывать ограничение по предельно допустимой шероховатость обработанной поверхности Ra:
 (5)
(5)где k0, k1, k2, k3, k4 – коэффициент и показатели, которые характеризуют сте-пень влияния подачи S, радиуса при вершине r, скорости V и переднего угла γ на шероховатость обработанной поверхности Ra.
Это ограничение необходимо представить в следующем виде:
 (6)
(6)
Математическая модель задачи оптимизации скорости резания и подачи при тонком точении представляется следующим образом:
 (7)
(7)
 (8)
(8) (9)
(9)
Согласно МГП на первом этапе оптимизации скорости резания и подачи решается система линейных уравнений (8), имеющая единственное решение:
 (10)
(10)Особенность МГП является возможность уже на первом этапе решения оценить вклад каждой составляющей целевой функции в общую себестоимость С - (3). Стоимость первой составляющей, связанной с машинной обработкой оценивается весомостью W01, а составляющей, связанной со сменой инструмента - W02.
Далее вычисляется экстремум целевой функции, для чего рассчитывается максимум двойственной функции V(W) - (7). На основании найденного экстремума целевой функции составляется система линейных уравнений для определения оптимальных режимов резания:
 (11)
(11)В результате решения этой системы определяются оптимальные подача S0 и скорость резания V0:
 (12)
(12)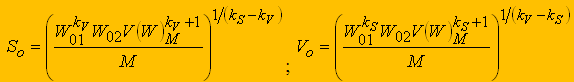 (13)
(13)
Примеры определения оптимальных режимов резания, обеспечивающих минимальную себестоимость, приведены для токарной обработки закаленной инструментальной стали Р18 (HRC 62-64) на токарно-винторезном станке с ЧПУ 16К20Ф3. Для этих условий принято: себестоимость станко - минуты А = 0,5коп/мин., стоимость одного периода стойкости инструмента Аи = 15 коп; время смены инструмента tc = 1мин.
Для тонкого точения используются резцы, оснащенные эльбором Р (передний угол γ = -10, радиус при вершине r = 0,5мм); глубина резания t = 0,5мм; требуемая шероховатость поверхности Ra = 0,63 мкм. Для указанных условий обработки принятые следующие коэффициенты и показатели: CТ = 2,8•104, kV = 0,65, kS = -0,52 [4].
Коэффициенты и показатели, которые характеризуют степень влияния подачи, переднего угла, радиуса при вершине и скорости резания на шероховатость обработанной поверхности: k0 = 0,68; k1 = 0,77; k2 = -0,28; k3 = -0,19; k4 = 0,66 [5]. Расчетные значения коэффициентов С01 = 392,7, СО2 = 4,557; С11 = 16,27. Коэффициенты весомостей, определенные в соответствие с формулой (10), равны: W01 = 0,28; W02 = 0,72, W11 = 0,85. Оптимальные значения подачи и скорости резания, рассчитанные в соответствие с формулами (13) равны: Sо = 0,084 мм/об, Vо = 54.2 м/мин.
Наличие аналитических зависимостей для определения оптимальных режимов резания существенно упрощает разработку рекомендаций по выбору рациональных условий обработки, что особенно актуально для тонкого точения.
Для тонкого точения оптимальная подача Sо увеличивается с увеличением шероховатости поверхности Ra и радиуса при вершине r; оптимальная скорость резания Vо увеличивается с увеличением радиуса при вершине r и уменьшается с увеличением шероховатости поверхности Ra (рис.1).

На основании установленных аналитических зависимостей для определения оптимальных режимов резания может быть рассчитан коэффициент изменения себестоимости обработки при отклонении выбранных режимов резания от их оптимального значения S = kS0, V=kV0. (k – степень отклонения):

 (14)
(14)
Из графика, представленного на рис. 2, следует, что минимальная себестоимость обработки имеет место при k = 1, то есть при оптимальных режимах резания. При отклонении режимов резания, как в меньшую, так и в большую сторону от оптимальных, себестоимость увеличивается.
Таким образом, представленная методика позволяет для любых условий тонкого точения выполнять расчеты оптимальных режимов резания, обеспечивающих минимальную себестоимость обработки.
На основании разработанной методики установлены закономерности изменения оптимальных значений подачи и скорости резания от шероховатости обработанной поверхности и радиусов при вершине.
Разработанная методика определения оптимальных режимов резания может быть широко использована для любых видов обработки.
При написании данного автореферата магистерская работа не является завершенной. Окончание планируется на декабрь 2010 года.