Summary of research and developments

INTRODUCTION

    Modern automated production, such as flexible manufacturing systems (FMS), as a stage of development production, not only did not lose its relevance as a basis of modern engineering, but also to reinforce it in force initially pledged principle of flexibility to build and operate. This principle meets modern conditions of the dynamic of the market, requiring frequent changing of our product range in the medium and small-scale production and reduce the time of their release , algorithms, decision-making and program management.

    Improving the quality of operational management is the most important factor for effectiveness of flexible manufacturing systems (FMS). As part of the operational management of one of the major problems is capacity planning equipment, ie determining the structure of complex technical devices (units) and the streamlining of operations at the selected structure of production modules (scheduling).

    Planning provides the interaction set of elements of the controlled object in order to achieve the set goals chief of which is to provide a consistent over time and route-oriented space motion parts and products in production. The significance and complexity of control problems due to their hierarchical structure, functional features, dynamic, effective use of expensive equipment.

    Intelligence and Scheduling , in fact, is organizing a link between the structure of FMS, taken at production of organizational features of functioning FMS elements, process (TP) producer nomenclature of parts and process control. Therefore the solution of tasks aimed at improving the functioning of the FMS is a highly topical issue. [1]

Aims and tasks of the work

    Aim is to solve important scientific and technical problem consisting in the creation of the job-shop sheduling for the automated machining of small series and individual productions that increase their effectiveness.

    To achieve this goal in the work should address the following main tasks:

• Formation of directed graph based on data on the production shop;
• hoosing the most appropriate modification of ant algorithms;
• Using the mathematical apparatus of ant algorithms to create equipment loading schedules.

Actuality of theme

    The quality of the functioning of modern production is largely determined by decisions taken at the time of scheduling and operational management. Along with improving the quality of planning decisions more stringent requirements are to reduce their terms of developing, improving the efficiency and management flexibility.

    To ensure high efficiency of production areas must be optimal scheduling of equipment. Consequently, the need to develop a computerized subsystem operational and scheduling of the production site engineering production to increase efficiency through the establishment of sub-optimal scheduling of work, based on selected criteria optimization.

Supposed scientific novation

    At the present time through the application of ant algorithm to obtain good results for these complex optimization problems as the traveling salesman problem, Transportation problem, task scheduling task graph coloring, quadratic assignment problem, the problem of optimization of network traffic, and others. Best ant algorithms have shown themselves in the problem of finding the shortest path on a graph, the appliance has reduced all of the problem. In our country, ant algorithms have not yet received the proper development and use, though should make their great potential for solving different kinds of problems. Perhaps this work will facilitate the increased use of ant algorithms for solving various problems, because very few domestic publications on this topic.

Survey of research and developments

At national level

    As a result of the search among the materials of the portal Masters DonNTU were found working Anton Glivka, Khaustova Darya, Elena Sergeeva, in which to consider a substantive issue of scheduling of various sectors. Of the scientific papers a teacher of our university on this topic were found working Alexandr Sekirin

    In general, Ukraine has been found a lot of work on related areas with developed subsystem. Can be identified as existing development on this topic: SPRUT-OKP and Zenith SPPS.

At global level

    Most of the works on this topic is foreign. We can conclude that in the west, the topic is much better developed, because there are constantly being improved means of production. Of foreign authors can be identified: M. Dorigo, G. Di Caro, Rong Zhou, Alan S. Manne. Of foreign ready systems can be distinguished: LEKIN и TACTIC.

    In general, deficiencies of both domestic and foreign systems is a high price and poor scalability.

Problem description

    The Job-Shop Scheduling Problem (JSP) can be characterized as n jobs to be processed on m machines. In general it is a set of concurrent and conflicting goals to be satisfied using a finite set of resources where resources are called machines and basic tasks are called jobs. Each job is a request for scheduling a set of operations according to a process plan which specifies precedence restrictions. We have

    

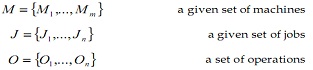
    For each operation there is a job to which it belongs, a machine on which it has to be run and a processing time of the operation , where is a nonnegative integer. Every job is a chain of operations and every operation has to be processed on a given machine for a given time. The task is to find the starting times of all operations such that the completion time of the very last operation is minimal. The chain order of each job has to be maintained and each machine can only process one job at the same time. No job can be preempted; once an operation starts it must be completed. The solution s to an instance of the n x m JSP specifies a processing order for all of the jobs on each machine and implicitly defines an earliest starttime and earliest completion time for each operation. The maximum of the completion times is called makespan and most research address the problem of makespan minimization.

    Given an instance of JSP we can associate with it a disjunctive graph G = (V, A, E), where V is the node set, A is the conjunctive arc set and E is the disjunctive arc set. The nodes V correspond to all of the operations and two dummy nodes, a source and a sink. The conjunctive arcs A represent the precedence relationships between the operations of a single job and the disjunctive arcs E represent all pairs of operations to be performed on the same machine. All arcs emanating from a node have the processing time of the operation performed at that node as their length. The source has conjunctive arcs with length zero emanating to all the first operations of the job and the sink has conjunctive arcs coming from all the last operations. A feasible schedule corresponds to a selection of one arc from each disjunctive arc pair such that the resulting directed graph is acyclic, i.e. no loops can be found. The problem of minimizing the makespan reduces to finding a set of disjunctive arcs which minimize the length of the critical path in the directed graph. [2]

Description of ant algorithms

    To solve this problem have been chosen ant algorithms , which are based on the population of potential solutions and developed to solve combinatorial optimization problems, above all, finding various ways to the graphs. Co-operation between individuals (artificial ants) are implemented on the basis of modeling “stigmergy”. Moreover, each agent, called artificial ants, looking for the solution of the problem. Artificial ants build a solution to the problem consistently, moving on to the count, laying pheromone and the choice of further stretch of track into account the concentration of this enzyme. The higher concentration of pheromone in the subsequent section, the more likely to select it.[3]

    As an illustration, take the task of finding the shortest path between two nodes of a graph G = (V, E), where V - the set of nodes (vertices) and E - the matrix that represents the connection between nodes. Let - the number of nodes in the graph. Let – the length of the path in the graph traversed by the k-th ant, which is equal to the number of arcs traversed (swings between peaks) from the first to the last vertex of the path. Example of a graph with a distinguished way shown in Figure 1. With each arc connecting vertices (i, j) associate the concentration of pheromone .

Figure 1 Example of progress on the graph (Animation: volume - 36Kb size - 407H264 the number of frames - 6, a delay between frames - 300 ms, the number of cycles of repetition - a continuous cycle of recurrence).

    Strictly speaking, initially the concentration of pheromone for each arc of the graph is zero, but for the convenience of each arc is assigned a small random number (0).

    An ant chooses a path next arc as follows. Set of ants are placed in the starting point. In each iteration , each ant incrementally constructs the path to the ultimate peak. At the same time in each node, each ant has to choose the next arc path. If an ant k located at the vertex i, it selects the next vertex on the basis of transition probabilities

(1)

    Where represents the number of possible vertices connected to vertex i, for ant k. If for any node i an ant k , then the predecessor node i is included in . In this case the path may loop. These loops are removed upon reaching the end of the city road. In (1) - a positive constant, which determines the effect of the concentration of pheromone. Obviously, higher values increase the effect of concentration of pheromone. When all ants have constructed a complete path from the initial to the final vertex is removed loops in the paths, and each ant marks its built path delay for each arc pheromone in accordance with the following formula

(2)

Here – дthe length of the path constructed k-th ant at time t. Thus, for each arc of the graph the concentration of pheromone is determined as follows

(3)

    where -number of ants. From (3) that the total concentration of pheromone to this arc is proportional to the “quality” ways, which includes this arc, since postponed reflects the “quality” of the path [5].

Conclusion

    In the course of work were analyzed existing approaches for solving problems of operational-calendar planning. Was developed algorithm for the formation schedule load of equipment, are selected optimization criteria and the criteria for stopping.

    Further actions are determined by the need to develop mathematical and algorithmic models of the functioning of the operational-calendar planning, and development of software architecture suitable for practical implementation of the system.

LIST OF LITERATURE

1. System is operational and scheduling of automated machining small batch production on the basis of complex models: Thesis Dr.Sci.Tech. Ravil Zagidullin: 05.13.06 Upha, 2006
2. Swarm Intelligence. Focus on Ant and Particle Swarm Optimization, 2007 I-Tech Education and Publishing.
3. Particle swarm algorithms, a course, Yuri Skobtsov, 2009
4. [202] M. Dorigo and G. Di Caro. The Ant Colony Optimization Meta-Heuristic. In D. Corne, M. Dorigo, and F. Glover, editors, New Ideas in Optimization, pages 11-32. McGraw-Hill, 1999.
5. Donald W. Fogarty, Yohn H. Blackstone, Yr. And Thomas R. Hoffman. Production and Inventory management (Cincinnati: South - Western Publishing, 1991). P. 452 - 453.
6. S.Shtovba Ant algorithms / / Exponental Pro. Mathematics in Applications, 2003, #4, P. 70-75
7. Official website СПРУТ-ОКП. URL: http://sprut.ru/productsandservices/mrpii
8. Official website Zenith SPPS. URL: http://www.zspps.com/soft.html
9. Personal website M. Dorigo. URL: http://iridia.ulb.ac.be/~mdorigo/HomePageDorigo/
10. List of scientific articles G. Di Caro. URL: http://www.idsia.ch/~gianni/my_publications.html
11. List of scientific articles Rong Zhou. URL: http://www2.parc.com/isl/members/rzhou/pub-cat.html
12. On the Job Shop Scheduling Problem. URL: http://ideas.repec.org/p/cwl/cwldpp/73.html
13. Official website LEKIN. URL: http://www.stern.nyu.edu/om/software/lekin/index.htm
14. Official website TACTIC. URL: http://www.waterloo-software.com/

At writing of this abstract of thesis master's degree work is not yet completed. Final completion: December, 2010. Complete text of work and materials on the topic can be got for an author or his leader after the indicated date.

© DonNTU 2010, Maxim Chorniy