В докладе, на примере многослойных полносвязных нейронных сетей рассматривается проблема долговременности их обучения. Предложены возможные методы увеличения скорости обучения сетей: управление процедурами вычисления и изменения весовых коэффициентов, реорганизация объектов в распознаваемых классах.

Искусственные нейронные сети находят все более широкое применение в решении задач искусственного интеллекта. Они уже доказали свою способность решать такие задачи как ассоциативный поиск, кластирование и распознавание образов.

На сегодняшний день в распоряжение разработчика предоставлено большое количество различных моделей нейронных сетей и алгоритмов их обучения [1, 2, 3]. И хотя постоянно ведутся научные исследования в области совершенствования существующих и создания новых моделей и обучающих алгоритмов, теория нейронных сетей пока остается слабо формализованной. Однако, уже на данном этапе четко прорисовываются два основных этапа создания нейронного вычислителя: структурный и параметрический синтез. В рамках первого этапа перед разработчиком ставятся задачи: определения модели сети, определение ее структуры, выбор алгоритма обучения. Параметрический синтез включает в себя процессы обучения нейронной сети и верификации полученных результатов. Причем в зависимости от результатов верификации возникает необходимость возврата на различные стадии структурного или параметрического синтеза, т.о. становится очевидной итеративность процесса проектирования нейронного вычислителя.

Слабая формализованность этих этапов приводит к тому, что разработчику, проектирующему нейронный вычислитель, приходится сталкиваться с решением некоторых проблем. Например, на этапе структурного синтеза, при проектировании нейровычислителя, решающего нестандартную задачу, приходится прилагать значительные усилия для выбора модели сети, её внутренней структуры и способа обучения. Проблемой параметрического синтеза сетей является трудоемкость их обучения. Если решать реальные задачи, учитывая все возможные факторы, то время обучения нейронной сети для такой задачи оказывается достаточно продолжительным. Но при решении некоторых задач требуется затратить как можно меньше времени на этот процесс, например, работа в реальном масштабе времени.

Данная статья ставит своей задачей предложить возможные методы уменьшения времени, затрачиваемого на обучение многослойных нейронных сетей с обратным распространением ошибки. В качестве таких методов предлагаются: управление процедурами изменения и вычисления весовых коэффициентов, реорганизация объектов в распознаваемых классах. В [4] были предложены два возможных пути решения этой задачи. Первый основывался на выборе определенного функционального базиса нейронной сети. Второй метод управлял значением шага изменения весов сети, рассматривая его с точки зрения центробежной силы и, корректируя его таким образом, чтобы его вектор всегда был направлен на оптимум множества весовых коэффициентов.

В предлагаемой работе поставленная задача рассматривается с точки зрения переобучения нейронной сети. В большинстве случаев нейронную сеть обучают, пока ее ошибка не станет равной нулю. Это приводит порой к неоправданным затратам драгоценных ресурсов времени, хотя для решения большей части задач достаточно, чтобы эта ошибка не превышала определенного значения.

Иногда степень достаточности определяется исходя из условий задачи и искомого результата. Однако, в большинстве случаев этот процесс протекает на интуитивном уровне и руководствующий принцип не фиксируется сознанием в достаточной мере. На самом деле этот момент является одним из самых важных в решении задач подобного типа, и оптимальное значение варьируемого параметра может зависеть от многих исходных величин и ограничений накладываемых на решение задачи. Таким образом, появляется необходимость в формализации данного принципа; в дальнейшем — Принципа Достаточности (ПД).

Обучение с учетом Принципа Достаточности

Как уже говорилось ранее, нейронные сети используются для решения ряда задач искусственного интеллекта. Рассмотрим обучение многослойной нейронной сети с обратным распространением ошибки в рамках решения задач классификации [5].

В процессе обучения нейронных сетей, в числе прочих, можно выделить два вида ошибки, назовем их глобальной и локальной. Выражение для вычисления локальной ошибки имеет следующий вид:

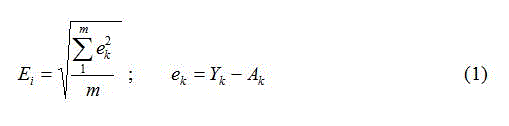
где e_k – элементарная ошибка k-го нейрона выходного слоя сети, m – число нейронов в выходном слое сети.

Глобальная ошибка сети вычисляется по следующей формуле:

где E_i – локальная ошибка нейронной сети на i-м наборе, n – число обучающих наборов.

Идеально обученной, считается такая сеть, которая полностью повторяет ОВ [6], т.е. ее глобальная ошибка равна нулю. Но обучение нейронной сети до такой степени представляет собой очень трудоемкую задачу, а нередко и вовсе неразрешимую. Эти трудности обычно связаны с тем, что разные классы имеют похожие объекты, и чем таких объектов больше и чем больше они похожи, тем труднее будет обучить нейронную сеть.

Суть ПД заключается в отказе от обязательного стремления к Идеалу при поиске решения конкретной задачи. Рассматривая эту проблему с точки зрения ПД в рамках глобальной и локальной ошибки, можно сказать, что далеко не всегда необходима 100%-я точность распознавания. Иногда, для того чтобы отнести исследуемый объект к заданному классу, достаточно, чтобы ошибка сети на данном наборе не превышала некоторого &delta.

В случае если оценка качества обученности сети ведется по глобальной ошибке, то по достижении заданного значения &delta, обучение сети должно будет прекратиться. Если же кроме этого рассматриваются и локальные ошибки, ПД работает следующим образом: если E_i &le &delta, то можно считать, что i-й объект был распознан успешно и на данной итерации пересчет весовых коэффициентов не производится. Самым нижним уровнем является рассмотрение элементарных ошибок e_k. В этом случае, если её величина укладывается в интервал &delta, то мы считаем что e_k=0 , и уже это значение ошибки нейрона используется алгоритмом обучения для формирования новых весовых коэффициентов сети.

Минимальное значение &delta зависит от характера обучающей выборки. В качестве параметров характеризующих ОВ рассмотрим ее полноту, равномерность и противоречивость. Полнота выборки характеризуется обеспеченностью классов обучающими наборами; количество обучающих наборов для класса должно в 3-5 раз больше, чем используемое в наборе число признаков класса [7]. Пусть величина, характеризующая полноту выборки, вычисляется следующим образом:

где N_F – число классов удовлетворяющих указанному условию, N – общее число классов.

Равномерность ОВ показывает, на сколько равномерно распределены обучающие наборы по классам. Для ее вычисления рассмотрим величину [C_i] – количество обучающих наборов для класса i , тогда среднее отклонение этой величины по выборке для данного класса будет вычисляться по формуле:

где k – количество классов. Вычислим мат-ожидания для величин &Delta _Ci и [C_i] при условии, что они равновероятны и назовем их соответственно R _&Delta и N_cp :

Тогда равномерность выборки будет вычисляться по формуле:

Противоречивость – это процент противоречивых наборов в ОВ; противоречивыми считаются наборы (объекты), обладающие одинаковыми признаками, но относящиеся к разным классам. Таким образом, противоречивость есть:

где N_ПР – число противоречивых наборов, N – общее число наборов в ОВ.

Очевидно, что чем меньше противоречивость ОВ и выше её равномерность, тем уже может быть интервал &delta.

Однако, в процессе обучения объекты классов, попадая в интервал &delta, ложатся неравноудаленно от Эталона класса (рис. 2.1). Дифференцирование этих ситуаций позволит улучшить качество обучения сети, поскольку позволит корректировать веса с учетом удаленности реакции сети от эталонной. В данном случае, расстояние до эталона будет определять величину градиента изменения веса. Для этого необходимо либо разбить область  на отрезки и каждому из них поставить в соответствие значение градиента (Рис. 2.2), либо задать на этом интервале функцию a(t)=F(x) (Рис. 2.3).

Таким образом, предполагалось уменьшить число итераций обучения нейронной сети при заданной точности распознавания элементов выборки. Результатом применения этого метода стало то, что функция ошибки сети E из колебательной становилась фактически монотонно убывающей.

Коррекция шага изменения весовых коэффициентов

В оригинальном варианте алгоритма обратного распространения ошибки [8] формула изменения весовых коэффициентов, для пары нейронов i, j (Рис. 1), выглядит следующим образом:

где E_j – ошибка j-го нейрона, A_i – уровень активации i-го нейрона, а &alpha – шаг изменения веса. Здесь &alpha – величина постоянная, однако очевидно, что если он будет слишком мал, то обучение будет проходить очень медленно. Если же &alpha велик — то, в момент достижения точки минимума (глобального или локального) функции ошибки E=f(W) (E – глобальная ошибка сети, W – множество весовых коэффициентов сети) (Рис. 2), сеть не сможет в нее попасть и будет бесконечно долго колебаться вокруг нее, производя бесконечные пересчеты множества весов и ухудшая свои показатели.

Таким образом, возникает необходимость управлять величиной &alpha . Очевидно, что если необходимо достигнуть оптимального множества весовых коэффициентов за минимальное количество итераций, то выбор некоторого среднего значения шага не является приемлемым. Целесообразно в момент начала обучения нейронной сети установить некоторое его максимальное значение, обеспечив, таким образом, быстрое приближение к области, где находится W_opt и, затем, постепенно уменьшать его по приближению к самой точке оптимума: &alpha ₀=0; &alpha _t+1 = &alpha _t - &part &alpha , где &part &alpha – декремент шага изменения весов сети.

Определение момента в процессе обучения нейронной сети, когда необходимо уменьшить величину шага, а также выбор значения &part &alpha для каждой задачи индивидуальны. Например, в решенной нами задаче прогнозирования остатков на банковском счете, опытным путем было установлено, что уменьшение &alpha целесообразно производить, если &Delta E < 0.1*10 ^-6 , а &part &alpha =0.001 . Использование такого условия позволило в течение всего процесса обучения сохранить достаточную скорость уменьшения ошибки.

Предлагаемый метод динамического управления шагом изменения весовых коэффициентов нейронной сети в процессе ее обучения позволяет обеспечить максимальную скорость уменьшения ошибки сети E на всех участках графика E=f(W).

Реорганизация распознаваемых классов

Еще одним методом ускорения обучения нейронных сетей является реорганизация множества распознаваемых классов. В зависимости от того, на сколько ОВ противоречива и неравномерна мы можем объединять классы между собой либо образовывать новые.

Рассмотрим ситуацию с неравномерной ОВ, здесь параметрами ПД выступают точность интерпретации исходных данных и размерность самой нейронной сети. Точность представления данных обуславливается формируемыми классами.

Для многослойных нейронных сетей типа Back Propagation зависимость этих характеристик заключается в следующем: количество распознаваемых классов однозначно определяет число нейронов в выходном слое сети, что косвенно определяет и количество нейронов в ее скрытых слоях. Таким образом, сокращение числа классов ведет к уменьшению размерности нейронной сети, а чем меньше сеть, тем быстрее она учится.

Однако большинство реальных задач, решаемых на нейронных сетях, не допускают таких потерь в точности классификации. Таким образом, этот метод может быть применен только для задач, не обладающих жесткими ограничениями по точности.

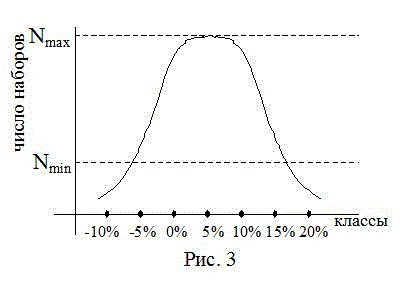
Уменьшать количество классов предлагается путем их объединения. Для выявления классов подлежащих объединению необходимо проанализировать построенную ОВ на предмет её равномерности и полноты. Если число обучающих наборов для некоторого класса не удовлетворяет условию полноты ОВ, либо оно значительно меньше, чем число наборов в других классах, то распознавание сетью этого класса будет затруднено. Примером результатов, полученных после анализа, может быть ситуация с классическим нормальным распределением, представленная на Рис. 3, где в качестве классов выбраны изменения некоторой величины в процентах. Для повышения равномерности ОВ выберем классы, обеспеченные обучающими наборами менее определенного N_min и склеим близлежащие классы. Число обучающих наборов полученных классов преодолеет порог N_min , и сеть сможет нормально и быстро обучиться. Однако, общее число распознаваемых классов уменьшится, что приведет к снижению точности нейронной сети в решении данной задачи. Таким образом, необходимо согласовать, используя понятие ПД, число классов, распознаваемых нейронной сетью, с её размерностью.

Формирование новых классов производится в седующих случаях:

1. если в классе кроме объектов, приближенных к эталону класса и имеющих низкую дисперсию – Правила, существуют объекты удаленные от эталона и (разрозненно) расположенные вблизи его границ – Исключения;

2. если дисперсия внутри класса велика и невозможно чётко определить эталон.

Исключения и нечёткие классы повышают противоречивость ОВ, их наличие может говорить о неверном разбиении пространства объектов на классы. Решением данной проблемы может быть перемещение Исключений в другие классы либо образование новых классов с меньшей величиной дисперсии.

Таким образом, мы можем повысить скорость обучения нейронной сети либо за счет сокращения числа распозаваемых классов, либо, понижая противоречивость ОВ путем перемещения объектов между классами и образуя новые классы. В первом случае скорость обучения увеличивается из-за уменьшения размерности нейронной сети, во втором – из-за повышения качества ОВ.

Итак, в статье было предложено три возможных способа увеличения скорости обучения многослойных нейронных сетей. Также отметим здесь, что способ [4], основанный на выборе функционального базиса нейронной сети, рассматривает эту проблему с точки зрения увеличения скорости вычислений. Описанные же в статье первые два метода рассматривают задачу ускорения обучения, как задачу уменьшения числа итераций обучения, а последний предполагает оба варианта. Исходя из этих предпосылок, можно сделать вывод о том, что в рамках быстрого развития современного аппаратного обеспечения, предложенные в данной работе методы являются более перспективными в проблеме ускорения обучения нейронных сетей.

Все представленные методы были успешно применены на практике, при решении задачи прогнозирования остатков на банковских счетах. Наибольший выигрыш в количестве итераций дали метод коррекции шага и сокращение числа распознаваемых классов. Так, коррекция величины шага позволила сократить число итераций на порядок, а время обучения практически в два раза.

Литература

1. В.А. Крисилов, Д.Н. Олешко, А.В. Трутнев. Применение нейронных сетей в задачах интеллектуального анализа информации. //Труды Одесского политехнического университета, Вып.2 (8). 1999, с. 134

2. Авеньян Э.Д. Алгоритмы настройки многослойных нейронных сетей.//Автоматика и телемеханика-1995-N 5. С.106-118.

3. Минский М., Пейперт С. Персептроны. М.: МИР, 1971. с. 261.

4. P. Patrick. Minimisation methods for training feedforward Neural Networks. //NEUARAL NETWORKS, 1994, Volume 7, Number 1, P. 1-11

5. Джеффри Е. Хинтон. Как обучаются нейронные сети.// В мире науки - 1992 - N 11 - N 12 - c. 103-107.

6. Rumelhart B.E., Minton G.E., Williams R.J. Learning representations by back propagating error.// Wature, 1986. V. 323. p. 1016-1028.