Исследуются вычислительные возможности искусственных нейронных сетей. В связи с этим происходит возврат к классическому вопросу о представлении функций многих переменных с помощью суперпозиций и сумм функций одного переменного и новая редакция этого вопроса (ограничение одной произвольно выбранной нелинейной функцией одного переменного).

Показано, что можно получить сколь угодно точное приближение любой непрерывной функции многих переменных, используя операции сложения и умножения на число, суперпозицию функций, линейные функции а также одну произвольную непрерывную нелинейную функцию одной переменной.

Для многочленов получен алгебраический вариант теоремы: любой многочлен может от многих переменных быть за конечное число шагов (точно) получен с использованием операций сложения умножения на число и произвольного (одного) многочлена от одного переменного степени выше 1.

Аппроксимационная теорема Стоуна переносится с колец функций на любые их алгебры, замкнутые относительно произвольной нелинейной операции, а также относительно сложения и умножения на число.

Для нейронных сетей полученные результаты означают: от функции активации нейрона требуется только нелинейность - и более ничего. Какой бы она ни была, можно так построить сеть связей и подобрать коэффициенты линейных связей между нейронами, чтобы нейронная сеть сколь угодно точно вычисляла любую непрерывную функцию от своих входов

Введение

В словах «искусственные нейронные сети» слышатся отзвуки фантазий об андроидах и бунте роботов, о машинах, заменяющих и имитирующих человека. Эти фантазии интенсивно поддерживаются многими разработчиками нейросистем: рисуется не очень отдаленное будущее, в котором роботы осваивают различные виды работ, просто наблюдая за человеком, а в более отдаленной перспективе . человеческое сознание и личность перегружаются в искусственную нейронную сеть . появляются шансы на вечную жизнь.

Если перейти к прозаическому уровню повседневной работы, то нейронные сети - это всего-навсего сети, состоящие из связанных между собой простых элементов - формальных нейронов. Значительное большинство работ по нейроинформатике посвящено переносу различных алгоритмов решения задач на такие сети.

Ядром используемых представлений является идея о том, что нейроны можно моделировать довольно простыми автоматами, а вся сложность мозга, гибкость его функционирования и другие важнейшие качества определяются связями между нейронами. Каждая связь представляется как совсем простой элемент, служащий для передачи сигнала. Предельным выражением этой точки зрения может служить лозунг: "структура связей . все, свойства элементов . ничто".

Совокупность идей и научно-техническое направление, определяемое описанным представлением о мозге, называется коннекционизмом (по-ангийски connection . связь). Как все это соотносится с реальным мозгом? Так же, как карикатура или шарж со своим прототипом-человеком - весьма условно. Это нормально: важно не буквальное соответствие живому прототипу, а продуктивность технической идеи.

С коннекционизмом тесно связан следующий блок идей:

1) однородность системы (элементы одинаковы и чрезвычайно просты, все определяется структурой связей);

2) надежные системы из ненадежных элементов и "аналоговый ренессанс". использование простых аналоговых элементов;

3) "голографические" системы . при разрушении случайно выбранной части система сохраняет свои полезные свойства.

Предполагается, что система связей достаточно богата по своим возможностям и достаточно избыточна, чтобы скомпенсировать бедность выбора элементов, их ненадежность, возможные разрушения части связей.

Коннекционизм и связанные с ним идеи однородности, избыточности и голографичности еще ничего не говорят нам о том, как же такую систему научить решать реальные задачи. Хотелось бы, чтобы это обучение обходилось не слишком дорого.

Существует большой класс задач: нейронные системы ассоциативной памяти, статистической обработки, фильтрации и др., для которых связи формируются по явным формулам. Но еще больше (по объему существующих приложений) задач требует неявного процесса. По аналогии с обучением животных или человека этот процесс называют обучением.

Обучение обычно строится так: существует задачник . набор примеров с заданными ответами. Эти примеры предъявляются системе. Нейроны получают по входным связям сигналы . "условия примера", преобразуют их, несколько раз обмениваются преобразованными сигналами и, наконец, выдают ответ . также набор сигналов. Отклонение от правильного ответа штрафуется. Обучение состоит в минимизации штрафа как (неявной) функции связей. Технике такой оптимизации и возникающим при этом задачам посвящена обширная литература (см. [1-3]).

Неявное обучение приводит к тому, что структура связей становится "непонятной". не существует иного способа ее прочитать, кроме как запустить функционирование сети. Становится сложно ответить на вопрос: "Как нейронная сеть получает результат?" . то есть построить понятную человеку логическую конструкцию, воспроизводящую действия сети. В последнее время все большее внимание привлекает вопрос: как сделать работу нейронной сети понятной - доступной явному описанию [3-6].

Среди задач, возникающих при изучении искусственных нейронных сетей, особое место занимает вопрос о пределах возможности этих систем: какие задачи они могут решать? Вопросы такого рода встают всегда при появлении новых моделей вычисления, универсальных по своему замыслу. Существует несколько вариантов утверждений о том, что нейронная сеть может вычислять любую функцию с произвольной наперед заданной точностью [7-10]. В данной работе вопрос о аппроксимационных возможностях нейронных сетей решается в более общем контексте и доказана теорема, единообразно охватывающая широкий спектр задач аппроксимации - от равномерного приближения функций многочленами до их аппроксимации искусственными нейронными сетями.

1. Элементы нейронных сетей

Для описания алгоритмов и устройств в нейроинформатике выработана специальная "схемотехника", в которой элементарные устройства . сумматоры, синапсы, нейроны и т.п. объединяются в сети, предназначенные для решения задач.

Интересен статус этой схемотехники . ни в аппаратной реализации нейронных сетей, ни в профессиональном программном обеспечении все эти элементы вовсе не обязательно реализуются как отдельные части или блоки. Используемая в нейроинформатике идеальная схемотехника представляет собой особый язык для представления нейронных сетей. При программной и аппаратной реализации описания, выполненные на этом языке, переводятся на языки другого уровня, более пригодные для реализации.

Важнейший элемент нейросистем - это адаптивный сумматор. Он вычисляет скалярное произведение вектора входного сигнала x на вектор параметров &alpha . На схемах будем обозначать его так, как показано на рис. 1. Адаптивным называем его из-за наличия вектора настраиваемых параметров &alpha .

Для многих задач полезно иметь линейную неоднородную функцию выходных сигналов. Ее вычисление также можно представить с помощью адаптивного сумматора, имеющего n+1 вход и получающего на 0-й вход постоянный единичный сигнал (рис. 2).

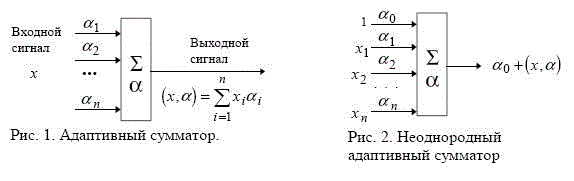
Нелинейный преобразователь сигнала изображен на рис. 3. Он получает скалярный входной сигнал x и переводит его в ϕ(x).

Точка ветвления служит для рассылки одного сигнала по нескольким адресам (рис. 4). Она получает скалярный входной сигнал x и передает его всем своим выходам.

Стандартный формальный нейрон составлен из входного сумматора, нелинейного преобразователя и точки ветвления на выходе (рис. 5).

Линейная связь - синапс - отдельно от сумматоров не встречается, однако для некоторых рассуждений бывает удобно выделить этот элемент (рис. 6). Он умножает входной сигнал x на «вес синапса» &alpha .

Также бывает полезно «присоединить» связи не ко входному сумматору, а к точке ветвления. В результате получаем элемент, двойственный адаптивному сумматору и называемый «выходная звезда». Его выходные связи производят умножение сигнала на свои веса.

Итак, дано описание основных элементов, из которых составляются нейронные сети.

2. Архитектура нейронных сетей

Как можно составлять сети из элементов? Строго говоря, как угодно, лишь бы входы получали какие-нибудь сигналы. Но такой произвол слишком необозрим, поэтому используют несколько стандартных архитектур, из которых путем вырезания лишнего или (реже) добавления строят большинство используемых сетей.

Сначала следует решить вопрос о том, как будет согласована работа различных нейронов во времени - вопрос о синхронности функционирования. Здесь и далее рассматриваются только нейронные сети, синхронно функционирующие в дискретные моменты времени.

Выделяется две базовых архитектуры нейронных сетей . слоистые и полносвязные сети.

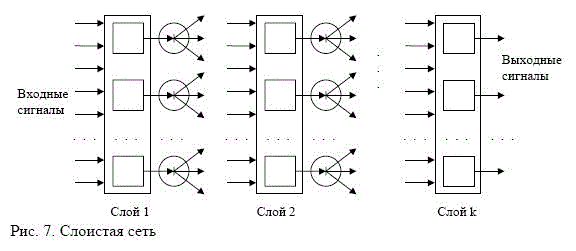
Слоистые сети: нейроны расположены в несколько слоев (рис. 7). Нейроны первого слоя получают входные сигналы, преобразуют их и через точки ветвления передают нейронам второго слоя. Далее срабатывает второй слой и т.д. до k-го слоя, который выдает выходные сигналы для интерпретатора и пользователя. Если не оговорено противное, то каждый выходной сигнал i-го слоя подается на вход всех нейронов i+1-го. Число нейронов в каждом слое может быть любым и никак заранее не связано с количеством нейронов в других слоях. Стандартный способ подачи входных сигналов: все нейроны первого слоя получают каждый входной сигнал. Особое распространение получили трехслойные сети, в которых каждый слой имеет свое наименование: первый . входной, второй . скрытый, третий . выходной.

Полносвязные сети: каждый нейрон передает свой выходной сигнал остальным нейронам, включая самого себя. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети. Все входные сигналы подаются всем нейронам.

Элементы слоистых и полносвязных сетей могут выбираться по-разному. Существует, стандартный выбор . нейрон с адаптивным неоднородным линейным сумматором на входе (рис. 5).

Для полносвязной сети входной сумматор нейрона фактически распадается на два: первый вычисляет линейную функцию от входных сигналов сети, второй . линейную функцию от выходных сигналов других нейронов, полученных на предыдущем шаге.

Функция активации нейронов (характеристическая функция) ϕ. нелинейный преобразователь, преобразующий выходной сигнал сумматора (см. рис. 5) . может быть одной и той же для всех нейронов сети. В этом случае сеть называют однородной (гомогенной). Если же ϕзависит еще от одного или нескольких параметров, значения которых меняются от нейрона к нейрону, то сеть называют неоднородной (гетерогенной).

Если полносвязная сеть функционирует до получения ответа заданное число тактов k, то ее можно представить как частный случай k-слойной сети, все слои которой одинаковы и каждый из них соответствует такту функционирования полносвязной сети.

Существенное различие между полносвязной и слоистой сетями возникает тогда, когда число тактов функционирования заранее не ограничено - слоистая сеть так работать не может.

Литература

1. Zurada J. M. Introduction to artificial neural systems. PWS Publishing Company,1992. 785 pp.

2. Haykin S. Neural networks. A comprehensive foundations. McMillan College Publ. Co. N.Y., 1994. 696 pp.

3. Горбань А.Н., Россиев Д.А. Нейронные сети на персональном компьютере. Новосибирск: Наука (Сиб. отделение), 1996. 276 с.

4. Le Cun Y., Denker J.S., Solla S.A. Optimal Brain Damage // Advances in Neural Information Processing Systems II (Denver 1989). San Mateo, Morgan Kaufman, 1990. P. 598-605/

5. Горбань А.Н. Обучение нейронных сетей. М.": изд. СССР-США СП "ParaGraph", 1990. 160 с. (English Translation: Traning Neural Networks // AMSE Transaction, Scientific Siberian, A, 1993, Vol. 6. Neurocomputing. P. 1-134).

6. Prechelt L. Comparing Adaptive and Non-Adaptive Connection Pruning With Pure Early Stopping // Progress in Neural Information Processing (Hong Kong, September 24-27, 1996), Springer, 1996. Vol. 1. P. 46-52.

7. Cybenko G. Approximation by superposition of a sigmoidal function. Mathematics of Control, Signals, and Systems, 1989. Vol. 2. PP. 303 - 314.

8. Hornik K., Stinchcombe M., White H. Multilayer feedforward networks are universal approximators. Neural Networks. 1989. Vol. 2. PP. 359 - 366.

9. Kochenov D.A., Rossiev D.A. Approximations of functions of C[A,B] class by neuralnet predictors (architectures and results). AMSE Transaction, Scientific Siberian, A. 1993, Vol. 6. Neurocomputing. PP. 189-203. Tassin, France.

10. Gilev S.E., Gorban A.N. On completness of the class of functions computable by neural networks. Proc. of the World Congress on Neural Networks (WCNN’96). Sept. 15-18, 1996, San Diego, CA, Lawrens Erlbaum Accociates, 1996. PP. 984-991.

11. Колмогоров А.Н. О представлении непрерывных функций нескольких переменных суперпозициями непрерывных функций меньшего числа переменных. Докл. АН СССР, 1956. Т. 108, №. 2 С.179-182.

12. Арнольд В.И. О функциях трех переменных. Докл. АН СССР, 1957. Т. 114, № 4. С. 679-681.

13. Колмогоров А.Н. О представлении непрерывных функций нескольких переменных в виде суперпозиции непрерывных функций одного переменного. Докл. АН СССР, 1957. Т. 114, № 5. С. 953-956.

14. Витушкин А.Г. О многомерных вариациях. М.: Физматгиз, 1955. 15. Stone M.N. The generalized Weierstrass approximation theorem. Math. Mag., 1948. V.21. PP. 167-183, 237-254.

15. Шефер Х. Топологические векторные пространства. М.: Мир, 1971. 360 с.