Одним из популярных сегодня подходов решения задачи прогнозирования является являестся использование искусственных нейронных сетей [1, 2]. В рамках этого подхода поведение некоторого процесса чаще всего преобразовывается во временной ряд, и далее нейронной сетью прогнозируется уже поведение этого временного ряда.

Однако, в большинстве задач прогнозирования разработчик сталкивается с непериодическими процессами, относительно быстро изменяющимися во времени. Такие изменения в поведении прогнозируемой величины требуют дообучения сети, а иногда и переформирования ее структуры. Существующие системы прогнозирования в большинстве оказываются неспособными работать с такими процессами. Это связано со значительным временем, которое они затрачивают на структурный и параметрический синтез нейронной сети. Например, в системе “Neuro Builder” [3] для выбора одной сети создается популяция нейронных сетей, насчитывающая более 1000 вариантов, из которых потом в процессе их обучения выбирается лучшая. При этом необходимо заметить, что обучение одной такой нейронной сети – это десятки часов машинного времени. Такие временные затраты недопустимы при прогнозировании быстроизменяющихся процессов, например, прогнозирование курсов ценных бумаг или поведения некоторого процесса на опасном производстве.

Существующие средства и подходы уменьшения времени обучения нейронных сетей [4] реализованы в основном только в системах моделирования, таких как “Neuro Shell”, “Neuro Solutions”. Однако эти подходы либо дают выигрыш во времени, но не дают возможность сети экстраполировать свои выводы за область известных данных (RBF сети) или имеют существенные ограничения на условия решаемой задачи либо на структуру нейронной сети (метод Левенберга-Маркара) [5]. Сами же системы моделирования из-за специфики своей направленности не могут быть использованы в качестве полноценных систем прогнозирования.

Анализ обучения нейронных сетей различными алгоритмами позволил выявить те аспекты данного процесса, которые в основном приводят к значительным затратам времени. Во-первых, это установка на получение как можно меньшей ошибки нейронной сети или вообще сведения ее к нулю, когда вполне достаточно было бы ограничиться некоторой заданной точностью распознавания. Во-вторых, при использовании классических подходов к обучению с постоянным шагом изменения весовых коэффициентов имеется высокая вероятность того, что данная величина шага не позволит нейронной сети попасть в точку оптимума. Это в свою очередь заставит сеть совершать бесконечные колебания вокруг этой точки. Наконец, обучающая выборка и множество распознаваемых классов могут быть построены слишком противоречиво и неравномерно. Это, в свою очередь, приведет к тому, что сеть будет обучаться очень долго и, в результате, просто не сможет выявить закономерности поведения процесса и решить поставленную ей задачу. В то время как реорганизация классов и наборов в выборке позволили бы ей качественно и быстро обучиться.

Настоящая работа посвящена решению актуальной задачи повышения скорости обучения нейронных сетей. В ней предложен ряд способов, позволяющих сократить время обучения при сохранении достаточной точности решения задачи. Это более гибкие процедуры вычисления весовых коэффициентов сети и улучшение характеристик обучающей выборки. Также рассмотрена система прогнозирования, в которой эти способы были реализованы.

Сокращение времени обучения нейронной сети

1. Принцип Достаточности

Для решения большей части задач достаточно, чтобы ошибка нейронной сети не превышала некоторого значения. Иногда степень достаточности определяется исходя из условий задачи и представления о качестве ожидаемого результата. Однако зачастую этот процесс протекает на интуитивном уровне, и руководствующий принцип не фиксируется в достаточной мере. На самом деле этот момент представляется одним из самых важных в решении задач подобного типа, и оптимальное значение варьируемого параметра может зависеть от многих исходных величин и ограничений, накладываемых на решение задачи. Таким образом, появляется необходимость в формализации данного принципа; в дальнейшем — Принципа Достаточности (ПД).

По сути ПД изменяет критерий оптимизации: целью уже не является точка искомого оптимума, а лишь некоторая ее окрестность, обеспечивающая достаточную точность решения конкретной задачи. Такой шаг позволяет существенно сократить время обучения сети. Далее предложено несколько подходов, позволяющих сократить обучение нейронной сети, опираясь на понятие достаточности.

2. Изменение весовых коэффициентов нейронной сети с учетом ПД

Рассмотрим обучение многослойной нейронной сети с обратным распространением ошибки в рамках решения задач классификации [6].

Процесс обучения нейронных сетей характеризуется рядом параметров. В числе прочих, можно выделить три вида ошибки, назовем их элементарной (e_k), локальной (E_i) и глобальной (E).

Элементарная ошибка – это ошибка нейрона выходного слоя на одной итерации обучения; локальная ошибка – ошибка нейронной сети на одном обучающем наборе, представляющая собой усредненное значение элементарных ошибок; глобальная ошибка – ошибка нейронной сети на всей ОВ, усредненное значение локальных ошибок.

Идеально обученной, считается такая сеть, глобальная ошибка которой равна нулю [7]. Но для реальных задач обучение нейронной сети до такой степени представляет собой достаточно трудоемкую задачу, а нередко и вовсе неразрешимую. Рассматривая эту проблему с точки зрения ПД в рамках глобальной ошибки, можно сказать, что далеко не всегда необходима 100%-я точность распознавания. Каждая конкретная задача имеет свои требования и ограничения по скорости и качеству обучения нейронной сети. Поэтому обучение предлагается проводить либо до момента успешного распознавания сетью всех наборов ОВ, либо по достижению некоторого достаточного значения функции ошибки.

Рассмотрим процесс обучения с другой точки зрения. Большинство используемых сегодня алгоритмов обучения нейронных сетей базируются на оценочной функции, которая дает представление о качестве работы всей сети в целом. При этом имеется некоторый алгоритм, который в зависимости от полученного значения этой оценки каким-то образом подстраивает изменяемые параметры системы. При этом производится пересчет всех параметров, в данном случае – весовых коэффициентов. Можно сказать, что такой подход к обучению обладает такой насыщенностью причинно-следственных связей, что одно событие неизбежно влечет за собой другое [8]. В данном случае изменение веса одной связи сети предполагает выполнение такой же процедуры и для всех остальных связей.

Однако анализ процессов обучения и функционирования реальных биологических систем показывает обратное. Мозг человека склонен к некоторому консерватизму и процесс обучения новым знаниям происходит таким образом, чтобы внести минимальные изменения в уже существующую структуру и максимально сохранить знания, накопленные ранее [9, 10]. При приобретении некоторого нового навыка мозг не переобучается полностью, а лишь изменяет характеристики некоторых своих связей. Таким образом, исходя из приведенных рассуждений, далее предложены еще два способа вычисления весовых коэффициентов нейронной сети.

В первом способе рассматривается локальная ошибка сети. Если E_i &le &delta (где &delta также некоторый критерий достаточности), то можно считать, что i-й объект ОВ был распознан успешно и на данной итерации пересчет весовых коэффициентов не производится.

Самым нижним уровнем является рассмотрение элементарных ошибок e_k. В этом случае, если её величина укладывается в интервал &delta , то мы считаем что e_k=0, и уже это значение ошибки нейрона используется алгоритмом обучения для формирования новых весовых коэффициентов сети. Таким образом, свои характеристики в сети изменят лишь некоторые связи, действительно требующие обучения.

Минимальное значение &delta зависит от характеристик ОВ. В качестве таких характеристик предлагается рассмотреть полноту и равномерность [11], а также противоречивость и повторяемость ОВ [12].

Полнота выборки определяется обеспеченностью классов обучающими наборами.

Равномерность ОВ показывает, на сколько равномерно распределены обучающие наборы по классам.

Противоречивость ОВ – показатель, характеризующий количество одинаковых объектов, принадлежащих к разным классам.

Повторяемость ОВ – показатель, характеризующий количество одинаковых наборов в рамках одного класса.

Однако формальная зависимость &delta от указанных характеристик ОВ не установлена и исследования в этой области заслуживают отдельного внимания и рассмотрения. Задача априорного определения величины &delta сводится к решению оптимизационной задачи по трудоемкости сравнимой с обучением нейронной сети. Исходя же из установленной качественной зависимости этих величин, можно утверждать, что чем меньше противоречивость ОВ и выше её равномерность, полнота и повторяемость тем уже может быть интервал &delta.

Таким образом, описанные подходы регулирования процесса обучения нейронной сети, позволяют уменьшить число итераций обучения нейронной сети при заданной точности распознавания элементов выборки. Результатом их применения стало то, что функция ошибки сети E из колебательной становится фактически монотонно убывающей.

3. Коррекция шага изменения весовых коэффициентов

В оригинальном варианте алгоритма обратного распространения ошибки [13] формула изменения весовых коэффициентов, для пары нейронов i, j, выглядит следующим образом:

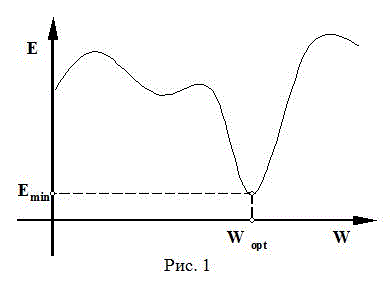
где e_j – ошибка j-го нейрона, A_i – уровень активации i-го нейрона, а &alpha – шаг изменения веса. Здесь &alpha – величина постоянная, однако очевидно, что если он будет слишком мал, то обучение будет проходить очень медленно. Если же &alpha велик — то, в момент приближения к точке минимума (глобального или локального) функции ошибки E=f(W) (E – глобальная ошибка сети, W – множество весовых коэффициентов сети) (Рис. 1), сеть не сможет в нее попасть и будет бесконечно долго колебаться вокруг нее, производя бесконечные пересчеты весовых коэффициентов.

Таким образом, возникает необходимость управлять величиной &alpha . Очевидно, что если необходимо достигнуть оптимального множества весовых коэффициентов за минимальное количество итераций, то выбор некоторого среднего значения шага не является приемлемым. В некоторых существующих системах моделирования искусственных нейронных сетей предложены варианты решения данной проблемы. Например, в пакете “NeuroShell” пользователь задает изначально некоторое значение декремента, на которое уменьшается на каждой итерации обучения. Однако такой подход является лишь частным случаем, поскольку нет необходимости в постоянном уменьшении величины шага. Уменьшать шаг необходимо лишь тогда, когда этого требует состояние процесса обучения.

Предлагается в момент начала обучения нейронной сети установить некоторое его максимальное значение, обеспечив, таким образом, быстрое приближение к области, где находится W_opt . А уменьшение &alpha ( &alpha ₀=0; &alpha _t+1 = &alpha _t - &part &alpha где &part &alpha – декремент шага изменения весов сети) производить в те моменты, когда ошибка начинает возрастать.

Эксперименты показали, что предлагаемый способ динамического управления шагом изменения весовых коэффициентов нейронной сети позволяет в процессе ее обучения обеспечить максимальную скорость уменьшения ошибки на всех участках графика E=f(W).

4. Реорганизация распознаваемых классов

Для качественного обучения нейронной сети желательно чтобы в ОВ все классы были обеспечены сравнимым количеством объектов (ОВ равномерная); не было одинаковых объектов в разных классах (ОВ непротиворечива) и объекты внутри классов имели низкую дисперсию и формировали четкий эталон. Однако на практике мы в основном сталкиваемся с противоположной ситуацией: количество объектов в одних классах на порядок больше, чем в других; в разных классах попадаются одинаковые объекты, либо существуют объекты в пограничной области соседствующих классов; объекты внутри класса разрознены либо образуют несколько удаленных областей с низкой дисперсией. А на подобных ОВ нейронные сети учатся долго и редко достигают необходимых показателей по достоверности.

В рамках решения задачи прогнозирования временных рядов, как задачи классификации, имеется некоторая свобода в формировании, как обучающих наборов, так и распознаваемых классов. Таким образом, один и тот же временной ряд может быть представлен обучающими выборками с разными характеристиками. Исходя из этого, в качестве еще одного способа ускорения обучения нейронных сетей предлагается реорганизация множества распознаваемых классов. В зависимости от того, на сколько ОВ противоречива и неравномерна, мы можем объединять классы между собой либо образовывать новые.

Введем следующие определения:

- объекты класса, имеющие низкую дисперсию и расположенные вблизи эталона либо формирующие этот эталон, назовем Правилами данного класса.

- объекты, удаленные от эталона, лежащие на границах класса, назовем Исключениями.

Теперь, исходя из этих определений, можно предложить критерии проведения реорганизации множества распознаваемых классов:

1. если в классе кроме Правил, существуют Исключения;

2. если дисперсия внутри класса велика, и невозможно чётко определить эталон.

Исключения и классы, не имеющие ярко выраженного эталона, понижают повторяемость ОВ, их наличие может говорить о неверном разбиении пространства объектов на классы. Решением данной проблемы может быть перемещение Исключений в другие классы либо образование новых классов с меньшей величиной дисперсии.

Кроме ускорения и повышения качества обучения путем улучшения характеристик ОВ с помощь реорганизации классов поставленную задачу можно решить и другим способом.

Для многослойных нейронных сетей с обратным распространением ошибки существует зависимость между количеством распознаваемых классов и размерностью сети. Количество распознаваемых классов однозначно определяет число нейронов в выходном слое сети, что косвенно определяет и количество нейронов в ее скрытых слоях. Следовательно, сокращение числа классов ведет к уменьшению размерности нейронной сети, а чем меньше сеть, тем быстрее она учится. Здесь параметрами ПД выступают точность представления исходных данных в ОВ (а следовательно и результирующая точность решения задачи) и размерность самой нейронной сети. Понятно, что объединение классов между собой дает выигрыш в скорости обучения, но приносит и потери в качестве.

Однако многие реальные задачи, решаемые на нейронных сетях, не допускают операций по реорганизации множества распознаваемых классов, и, как следствие, этот метод не может быть применен для решения таких задач.

Таким образом, скорость обучения нейронной сети можно повысить либо за счет сокращения числа распознаваемых классов, либо, повышая качество характеристик ОВ, перемещая объекты между классами и образуя новые классы. При этом необходимо руководствоваться понятием достаточности, выбирая соотношение скорости и качества решения задачи.

Описанные в данном разделе способы ускорения обучения нейронной сети типа Back Propagation нашли свое применение в системе прогнозирования поведения сложных процессов «FORECAST».

Литература

1. В.А. Крисилов, Д.Н. Олешко, А.В. Трутнев. Применение нейронных сетей в задачах интеллектуального анализа информации.// Труды Одесского политехнического университета, Вып.2 (8). 1999, с. 134

2. Роберт Хехт-Нильсен. Нейрокомпьютинг: история, состояние, перспективы.// Открытые системы, N4, 1998.

3. Neuro Builder 2001 – новое поколение нейросетей для финансовых аналитиков// http://www.neuroproject.ru/index.html

4. P. Patrick. Minimisation methods for training feedforward Neural Networks. //NEUARAL NETWORKS, 1994, Volume 7, Number 1, P. 1-11

5. Нейронные сети. STATISTICA Neural Networks.// М.: Горячая линия–Телеком, 2000 г. с.182.

6. Авеньян Э.Д. Алгоритмы настройки многослойных нейронных сетей.//Автоматика и телемеханика-1995-N 5. С.106-118.

7. Джеффри Е. Хинтон. Как обучаются нейронные сети.// В мире науки - 1992 - N 11 - N 12 - c. 103-107.

8. Садовой А. В., Сотник С. Л. Алгоритмы обучения нейронных сетей будущего// http://www.alicetele.com/~sergei/articles/algo/algo.htm

9. Дж. Экклс Физиология нервных клеток.// М., 1959

10. А.П. Быков, А.В. Вейц От нейрона к искусственному мозгу.// М.: НАУКА, 1971. с. 127

11. Крисилов В.А., Олешко Д.Н., Лобода А.В. Методы ускорения нейронных сетей.// Вестник СевГТУ. Информатика, электроника, связь, Вып. 32, 2001, с. 19

12. Тарасенко Р.А., Крисилов В.А. Предварительная оценка качества обучающей выборки для нейронных сетей в задачах прогнозирования временных рядов.// Труды Одесского политехнического университета, Вып.1 (13). 2001, с. 90

13. Rumelhart B.E., Minton G.E., Williams R.J. Learning representations by back propagating error.// Wature, 1986. V. 323. p. 1016-1028.