Аннотация

В данной статье рассматривается схема для прогнозирования временных рядов с помощью нейронных сетей. Эта схема состоит из трех этапов: выявление входных сигналов, определение числа нейронов в скрытом слое (s), а также прогнозирующей нейронной сети. В фазе обнаружения, автокорреляционный анализ используется для определения входных сигналов временных рядов для обучения нейронной сети. Определение количества нейронов в скрытом слое происходит с использованием правил Баума-Хаасслера. Рассчитывается число нейронов скрытых слоев и определяется модель входных данных, которые затем используются для построения прогнозирующей нейронной сети. Далее создана компьютерная модель, чтобы продемонстрировать эффективность системы.

Введение

Выявление тенденций и закономерностей в финансовых данных представляет большой интерес для деловых кругов в поддержку процесса принятия решений. До сих пор основным средством выявления тенденций и моделей были статистические методы, такие как статистическая кластеризация и регрессионный анализ [1,7]. Математические модели, связанные с этими методами экономического прогнозирования, тем не менее, линейны и не всегда могут прогнозировать поворотные точки экономических циклов [8], потому что во многих случаях модель данных может быть абсолютно нелинейной.

Новое поколение методологий, включая нейронные сети, системы знаний и генетические алгоритмы, привлекли к себе внимание для анализа тенденций и моделей. В частности, нейронные сети широко используются для финансового прогнозирования на фондовых биржах, иностранной валюты, будущего торговли сырьевыми товарами и доходности облигаций.

Большого внимания заслуживает прогноз фондовой области финансового прогнозирования [11]. В финансовой теории, гипотеза эффективного рынка (ГЭР), в его слабой форме, предсказывает, что просто анализ временных рядов данных не обеспечит доходность стратегии купли-продажи. Тем не менее, он не отрицает, что такой прогноз возможен с использованием внутренней информации. Предсказуемый успех с помощью нейронной сети и одномерных временных рядов противоречило бы этой форме ГЭР. Исследования с использованием нейронных сетей была проведена для получения тенденций фондовых рынков [9, 10, 12, 13]. Следует отметить, что многое в этой области остается конфиденциальным, возможно, из-за опасений потери конкурентного преимущества за счет владельцев.

Применение нейронных сетей в прогнозировании временных рядов [9, 10, 12, 13], основано на способности нейронных сетей аппроксимировать нелинейные функции. Самая популярная обработка исходных данных - обучение нейронных сетей либо данными за каждое наблюдение, либо данными за несколько последовательных удачных наблюдений. Обозначим данные в момент А как y(k), где у может быть вектором, тогда предобработка может быть описана как

или

соответственно, где NN() выступает за предсказание нейронной сети и l это число последовательных наблюдений. Эта процедура считает временные ряды нелинейными и имеет тенденцию приводить к нелинейной "авто-регрессии" модели соответствующей выборки. До сих пор было немного статей, описывающих, как выбрать материалы для прогнозирующей нейронной сети в целях обеспечения лучшей производительности прогнозирования. Мы убеждены в том, что производительность прогноза нейронной сети значительно зависит от модели входных данных .

Автокорреляционный анализ часто используется в прогнозирования временных рядов с использованием статистических подходов, таких как модели ARMA. Этот анализ используется главным образом в выявлении автокорреляции между последовательными значениями временных рядов, и используется в известных моделях ARIMA и Бокса-Дженкинса, которые являются очень эффективными в прогнозировании линейных временных рядов [7].

Автокорреляционный анализ может быть использован для определения правильной модели входных данных для нелинейного прогнозирования временных рядов с использованием нейронных сетей. Эта статья представляет собой схему для прогнозирования временных рядов с использованием нейронных сетей. Схема содержит три этапа: обнаружение входных сигналов, определение числа нейронов в скрытом слое (s), а также создание прогнозирующей нейронной сети. В фазе обнаружения, автокорреляционный анализ используется для определения входных сигналов временных рядов для обучения нейронной сети. Определение количества нейронов в скрытом слое происходит с использованием правил Баума-Хаасслера. Прогнозирующая нейронная сеть затем строится с определенной моделью входов и числом нейронов в скрытом слое (s). Индекс Hang Seng используется для иллюстрации применения этой схемы.

Эта статья организована следующим образом. В разделе 2 предложена схема прогнозирования временных рядов. В разделе 3 представлены результаты моделирования, чтобы продемонстрировать эффективность предлагаемой модели. Полученные результаты сравниваются с другими прогнозами. Прогнозирующие нейронные сети рассматриваются в двух ситуациях: краткосрочного прогнозирования и долгосрочного прогнозирования. В разделе 4 представлены наши выводы.

Схема для прогнозирования временных рядов с помощью нейронной сети

Нейронные сети с прямой связью состоят из слоев нейронов, в которых входной слой нейронов связан с выходным через один или несколько промежуточных слоев нейронов. Процесс обучения нейронной сети предполагает корректировку весов до получения желаемого отношения ввода / вывода. Большинство алгоритмов обучения, основанны на алгоритме обратного распространения Уидроу-Гоффа [15, 16]. Прогнозирующая нейронная сеть может быть описана следующим образом:

где z либо оригинальные наблюдения, либо обработанные данные

- остатки. Обработка входных данных, а также ряда e и z необходимо для определения эффективности прогноза.

В этой статье мы предлагаем схему прогнозирования временных рядов с использованием нейронной сети с прямой связью. Схема включает три этапа:

• Обнаружение фазы входных сигналов.

• Определение количества нейронов в скрытом слое (s).

• Создание прогнозирующей нейронной сети.

Подробное обсуждение каждого этапа представлено в следующих разделах.

Определение входных сигналов

Выявление входной схемы производится с помощью автокорреляционного анализа. В приложении дается краткое описание автокорреляционного анализа.

Выявление включает два этапа:

Шаг 1

Для данного временного ряда, вычисляются коэффициенты автокорреляции. Если обнаруживается тенденция, то используется дифференцирование для удаления этой тенденции. Этот шаг нужно повторять пока тенденция не удалится в разумной мере. Этот шаг важен, так как коэффициенты автокорреляции могут быть использованы для определения отставания остатков для краткосрочного прогноза.

Шаг 2

Расчет парциальных коэффициентов автокорреляции. Эта информация покажет, как автокоррелирует в . Выберите те частичные коэффициенты автокорреляции, которые значительно отличаются от остальных коэффициентов. Крупнейшее отставание между любыми двумя из коэффициентов это количество входов, необходимых для нейронной сети.

Определение количества нейронов в скрытом слое (s)

Число нейронов в скрытом слое связано с применением нейронных сетей для прогнозирования временных рядов. Правило большого пальца [5], известное как правило Баума-Хасслера, используется для определения количества скрытых нейронов, которые будут использоваться:

где количество скрытых нейронов,- это число обучающих примеров,- это ошибка терпимости,- количество точек данных в течение одного учебного примера, и - количество выходных нейронов.Это правило обычно гарантирует, что нейронные сети будут обобщать, а не запоминать.

Создание прогнозирующей нейронной сети

На основании входных сигналов определяется в § 2,1, а число нейронов в скрытом слое определяется в разделе 2.2, мы можем построить прогнозирующую нейронную сеть.

Есть два случая, которые должны быть рассмотрены в прогнозировании временных рядов: краткосрочное прогнозирование и долгосрочное. Под краткосрочным прогнозированием мы имеем в виду, что прогнозирующая нейронная сеть действительно предсказывает на один шаг вперед.

С определенными входными сигналами и числом нейронов в скрытом слое (s), мы предлагаем нейронную. сеть для краткосрочного прогноза, как показано на рисунке 1, в котором представляет собой задержку оператора, то есть. Эта структура отличается от других прогнозирующих нейронных сетей тем, что остатки рассматриваются таже как входные данные. Эта структура создана благодаря механизмам обычных статистических моделей прогнозирования, таких как модели ARIMA, которые воспринимают, прогноз как решение, принятое на основе нескольких предыдущих последовательных фактических наблюдений и остатков, разницы между фактическими наблюдениями и прогнозами.

Долгосрочный прогноз имеет большое значение в определении будущей динамики временных рядов, которые необходимо прогнозировать на несколько шагов вперед. Остатки более не доступны, а фактические данные в будущем, не известны. Для долгосрочного прогнозирования, из-за недоступности остатков, "обратная связь" от выхода на рисунке 1 должна быть удалена. Подготовка долгосрочных прогнозов не включает в себя остаточные сроки - это, несомненно, отличие от подготовки краткосрочных прогнозов.

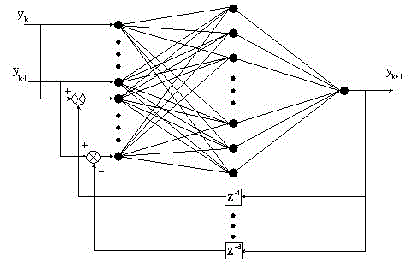
Рисунок 1: Прогнозирующая нейронная сеть для краткосрочного прогнозирования

Литература

1. Hanke J. E. & Reitsch A. G. (1984), Business Forecasting, 2nd Edition, Allyn and Bacon.

2. Yong T. P. (1993), "Using Neuro Forecaster for time series forecasting", Proceedings of First Symposium on Intelligent Systems Applications, Singapore, pp. 182-189.

3. Eberhart R. C. & Dobbins R. W. (1990), Neural Network PC Tools - A Practical Guide, San Diego: Academic Press.

4. SYSTAT (1990) Intelligent software, Systat Inc., IL 60201-3793, US.

5. Baum E. B. & Haussler D. (1988), "What size net gives valid generalization?", Neural Computation, 1, pp. 151-160.

6. Makridakis et al. (1983), Forecasting: Methods and Applications, New York: Wiley.

7. Jarrett J. (1991), Business Forecasting Methods, Basil Blackwell.

8. Ling C. S. (1993), "Choosing the right neural network model for trading", Proceedings of First Symposium on Intelligent Systems Applications, Singapore, pp. 26-33.

9. Wang H. A. & Chan A. K.-H. (1993), "A feedforward neural network model for Hang Seng Index", Proceedings of 4th Australian Conference on Information Systems, Brisbane, pp. 575-585.

10. Windsor C. G. & Harker A. H. (1990), "Multi-variate financial index prediction - a neural network study", Proceedings of International Neural Network Conference, Paris, France, pp. 357-360.

11. Jagielska I. (1993), "The application of neural networks to business information systems", Proceedings of 4th Australian Conference on Information Systems, Brisbane, pp. 565-574.

12. White H. (1988), "Economic prediction using Neural Networks: The case of the IBM daily stock returns", Proceedings of IEEE International Conference on Neural Networks, pp. 451-458.

13. Rao V. B. & Rao H. V. (1993), Neural Networks and Fuzzy Logic, MIS Press.

14. Goodman P., Rosen D. & Plummer A. (1993), NevProp Version 1, University of Nevada.

15. Widrow B. & Winter R. (1988), "Neural nets for adaptive filtering and adaptive patter recognition", Computer, 12, pp. 25-39.

16. Rumelhart D. E., McClelland J. L. & the PDP Research Group (1986), Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1, Cambridge: MIT Press.