Today solids processes are involved into most processes in chemical industry. The development of more effective control strategies and optimization of the production process can be provided using the simulation study of particle dynamics. In this contribution a concept of the developing Discrete Element Simulation environment for granular materials is presented.

            The Discrete Element Method (DEM), originally developed by Cundall and Strack [5], is the most powerful tool for computing the dynamics of a large number of particles of micron-scale size and above. DEM is based on the statement that each solid particle is represented as one separate entity and its motion and interactions are calculated with equations of Newton and Euler (Eq. 1-2).

		(1)
		(2)

            The force F and the torque M acting on a particle i of a mass m_i which has a position with the radius vector r_i and the angular orientation φ_i. The moment of inertia J_i is given as:

(3)

where L is a length dimension taken from the centre of mass (the radius of a spherical particle), c is the inertial constant (c = 2/5, if the object is a sphere and c = 1/2, if the object is a cylinder or disk rotating around its center). The contact condition between the particles is the following:

(4)

where s_ij is the overlap of particles, R_i and R_j are the particles radii (Fig. 1). If the condition of contact is fulfilled, then contact force will be calculated. The contact between the particles is described by collision models.
            In recent years a set of different commercial and open-source systems for DEM simulation have been developed. Their comparison is presented in the Table 1. Nevertheless, further analysis has shown that neither of existing open-source systems can be effectively applied for granular processes. The main purpose of the represented project is to develop a novel parallel cross-platform system for DEM simulation of the solid processes with a good agreement with experimental data.

Table 1

Comparison of the existing DEM simulation environments

	EDEM	PFC 3D	Chute maven	ELFEN	Passage	Ascalaph	Yade	LAMMPS	Pasimodo	Esys-Particle
Commercial	+	+	+	+	+	+	-	-	-	-
Parallelization	+	+	-	+	-	+	+	+	+	+
Coupling CFD	+	-	-	-	-	-	+	+	-	-
Coupling FEM	+	-	-	+	-	-	+	+	-	-
CAD import	+	-	+	+	-	-	-	+/-	-	-
Contact model variety	+	+	-	+	+	+	-	+	+	+
Adjust particle shape	+	+	-	+	+	+	+	+	+	-
3-D	+	+	+	+	+	+	+	+	+	-
Particles information	+	+	+	+	+	+	+	+	+	-

Figure 1 — Soft sphere model collision scheme

            There exist two major strategies of particle interaction handling: soft and hard sphere models. Hard sphere model is used more often for modeling dilute and energetic granular flows. For the implementation of more realistic simulations the soft sphere model is used (Fig.1) [8].
            The forces acting on the particle can be described depending on the material behaviour of particle during the impact. The contact force is divided into normal (Eq. 5, 6, 8) and tangential parts (Eq. 10, 12). The normal force can be divided into elastic and dissipative parts.

(5)

where k and are the elastic and dissipative constants. s is the overlap in normal direction. The conservation part (elastic) of the normal force by Hertz [1] and dissipative part (viscose) by Brilliantov [6] are presented in Eq. 6:

(6)

where E* — effective Young modulus of contact partner (index i and j), R* — effective radius, n — Poisson ratio, Ad — function of material viscosity:

(7)

h is damping coefficients of collision partners. E is Young’s modulus of a particle.
Note that in Eqs. (6-7) E_i = E_j = E*, n_i = n_j.
Nonlinear model of normal force by Kuwabara and Kono [3] is given:

(8)

Linear model of normal force by Walton and Braun [7] is given as follows:

(9)

where l, u — indexes of load and unload state of particles, k_l, k_u — the spring stiffness during loading and unloading state. s₀ the maximum resulting deformation of the impacting particles.
Model of tangential force by Haff and Werner [1] is presented as:

(10)

where is the relative velocity of the centers of the spheres (Eq. 11). are damping coefficients for normal and tangential force, m is friction coefficient.

(11)

Linear model by Di Maio and Di Renzo [2]:

(12)

where k^t is tangential stiffness. s^t is the displacement in tangential direction:

(13)

            The best agreement with experimental data showed the extended linear model by Walton and Braun [3]. Moreover, the linear model reduces the computational costs in comparison with non-linear models. One of tangential models that showed the best agreement with experimental data is linear model presented by Di Maio and Di Renzo [2].

            The integration of Newtonian equations of motion can be implemented with the help of Gear’s Integration scheme. The Gear algorithm (Fig. 2) is particularly suited for this problem, mainly because of its numerical stability [1].

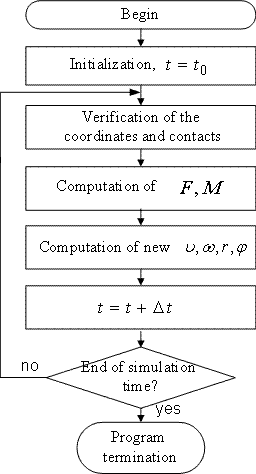Figure 2 — Gear’s integration scheme

First the predictor computes the particle positions, velocities, and higher-order time derivatives at time t+Δt by extrapolating the present values using a Taylor expansion (Eq. 14).

		(14)

After that the predicted coordinates and time derivatives are used for the computation and . From the forces and torques, the linear and angular accelerations and are obtained (Eq. 15).
To speed-up the calculation an algorithm of collision detection based on Verlet lists has been implemented.

(15)

            In this algorithm the forces are computed between the particles, that are close neighbours, i.e. the distance between them is less than verlet distance (Eq. 16)

< verlet distance

(16)

            The Verlet list is built for each single particle and it contains the indexes of neighbour particles. A double inclusion into the Verlet list is avoided because of the restriction that the particle with index i contains only neighbours with index j < i. The lists have to be rebuilt only in the case when the particle has moved to the distance that equals a half of the verlet distance.
             The grid divides the simulation area into cells. The size of a cell has to be larger than the largest particle. The condition (Eq. 16) is only verified for particles in the neighbouring cells.
            In case the particles are moving towards each other with the maximum speed, they can collide not being in the Verlet list. So it is necessary to save particles' positions and lists of neighbours when the new Verlet list is composed. In the worst case the simulation has to be returned to the step where the last successful list was made and continue with an increased Verlet distance.
            In addition to optimization algorithms the parallelization can be used to speed-up computations.

            Due to large quantities of particles that should be simulated, the development of effective parallelization strategy plays an important role. For this purpose the whole simulation volume is divided into a set of overlapped cells. Afterwards the computations are parallelized accordingly to the volume distribution. All particles in a cell or in a group of cells are calculated independently on a separate processor.
            The efficiency of a parallelization strategy depends on minimization of two main criteria: load imbalance and data transfer. By minimizing the load imbalance, the computations should be equally distributed between different processors. This can be reached by usage of non-constant grid size, where the size of each grid cell is proportional to the number of particles in the cell (Fig. 4). The minimization of data transfer between different processors can be reached by introduction of a grid with moving boundaries. The migration of particles between the processors can be minimized if the grid moves in the same direction as the main particle flow.
            The main part of the computer time in the simulation of granular materials is spent on vector operations. Usage of SSE (Streaming SIMD Extensions) instructions can make the computations with vectors and matrices up to 4 times faster.

            In the Fig. 4 the filling and release of a closed hopper in two and three dimensions are represented. On the third sketch the back wave from an impact is shown. On the fourth sketch the simulation is made periodic, i.e. particles falling out of the hopper are thrown back into it. The walls of the hopper are made from the same particles, but static.

Figure 4 – DEM-simulations of the particle filling and flow in a hopper in 2D and 3D
Animation parameters: number of frames: 6; number of cycles: 7; size: 39 Кб; Made in AVI->GIF Converter & GIF-Animator

            The simulation of granular materials in the micro-level gives a possibility to predict their macro-behaviour, analyze the influence of different process parameters and develop control strategies. The soft sphere model implemented in DEM simulation describes the collisions between the particles a lot more optimally than the hard sphere model.
            Simultaneously to the Gear's algorithm the optimization of the calculations can be performed using the Verlet lists. Additionally developed parallelization strategy can give a good speed-up factor and can be effectively used in networks of standard computers.

            1. T. Poeschel, T. Schwager. Computational granular dynamics. Models and algorithms. Springer, 2005.
            2. H. Kruggel-Emden, S. Wirtz, V. Scherer. A study on tangentional force laws applicable to the discrete element method for materials with viscoelastic or plastic behaviour, Chemical Engineering Science 63, 2008, 1523-1541.
            3. H. Kruggel-Emden, E. Simsek, S. Rickelt, S. Wirtz, V. Scherer. Review and extension of normal force models for DEM, Powder Technology 130, 2007, 157-173.
            4. S. Antonyuk, M. Khanal, J. Tomas, S. Heinrich and L. Moerl. Impact breakage of spherical granules: experimental study and DEM simulation, Chemical Engineering and Processing 45, 2006, 838-856.
            5. P.A. Cundall, O.D.L. Strack. A discrete numerical model for granular assemblies. Geotechnique 29, 1979, 47-65.
            6. N.V. Brilliantov, F. Spahn, J.-M. Hertzsch, T. Poeschel. Model for collision in granular gases, Physical review E, Vol. 53, 1996.
            7. Walton, O.R., Braun, R.L. Viscosity, granular-temperature, and stress calculations for shearing assemblies of inelastic, frictional disks. Journal of Rheology, 30, 1986, 949- 980.
            8. Antonyuk, S., Palis, S., Heinrich, S. Breakage behaviour of agglomerates and crystals by static loading and impact, Powder Technology, Special Issue: Agglomeration, in Press, February 2010.
            9. Poschel, T., Saluena, C., Schwager, T., 2001. Scaling properties of granular materials. Physical Review E 64 (1), (Art. No. 011308 Part 1).
            10. Schaefer, J., Dippel, S., Wolf, D.E., 1996. Force schemes in simulations of granular materials. Journal De Physique I 6 (1), 5–20.

---

            By this time the master work is not finished yet. Final completion date is: December 2010. For the full text and materials of this master work contact the author or his supervisors after the specified date.