На сьогоднішній день процеси твердих тіл втягнуті у більшість процесів хімічної індустрії. Розробка більш ефективних стратегій контролювання та оптимізації процесса виробництва¬ можуть зупроводжуватися моделюванням динаміки часток. У цій статті представлений концепт розробки середовища моделювання на осснові методу Дискретного елемента для сипких матеріалів.

            Метод дискретного елемента (DEM), розроблений Канделом і Стреком [5], є найбільш потужним інструментом для розрахунку динаміки великої кількості часток розміру мікрон і більше. DEM заснований на тому, що кожна тверда частка розглядається, як окемий об’єкт і її рух та взаємодія розраховуються за рівняннями Ньютона та Ейлера (Рів. 1-2).

		(1)
		(2)

            Сила F і момент M, діючі на частку i маси m_i яка має позицію з радіус вектором r_i також кут поверту у просторі φ_i. Момент інерції J_i представлений:

(3)

де L — довжина вимірювання узята від центру маси (радіус сферичної частки), c — константа інерції (c = 2/5, якщо об’єкт є сферою та c = 1/2, якщо об’єкт є циліндром або диском, який повертається навколо його центру). Умова контакту часток наступне:

(4)

де s_ij — пересічення часток, R_i и R_j — радіуси часток (рис. 1). Якщо умова контакту виконується, то сила взаємодії розраховується. Контакт часток описується моделями колізій.
            У останній час були розроблені різноманітні комерційні та відкриті бескоштовні системи для DEM моделювання. Їх порівняння приведено у табл. 1. Подальший аналіз показав, що жодна з існуючих систем з відкритим кодом не може бути ефективно застосована для моделювання процесів сипких матеріалів. Головною метою представленого проекту є розробка нової паралельної крос-платформної системи для DEM моделювання процесів твердих тіл з хорошим співвідношенням з експериментальними даними.

Таблиця 1

Порівняння існуючих середовищ DEM моделювання

	EDEM	PFC 3D	Chute maven	ELFEN	Passage	Ascalaph	Yade	LAMMPS	Pasimodo	Esys-Particle
Комерційна	+	+	+	+	+	+	-	-	-	-
Розпаралелювання	+	+	-	+	-	+	+	+	+	+
Сумісність з CFD	+	-	-	-	-	-	+	+	-	-
Сумісність з FEM	+	-	-	+	-	-	+	+	-	-
Імпорт CAD	+	-	+	+	-	-	-	+/-	-	-
Різні контактні моделі	+	+	-	+	+	+	-	+	+	+
Установка форм часток	+	+	-	+	+	+	+	+	+	-
3-х мірність	+	+	+	+	+	+	+	+	+	-
Інформація про частки	+	+	+	+	+	+	+	+	+	-

Рисунок 1 — Схема колізії моделі пружних сфер

            Існують дві основні стратегії зіткнення часток: пружна і тверда модель сфер. Модель твердих сфер найчастіше використовується для моделювання розріджених енергетичних потоків часток. Для виконання реалістичнішого моделювання використовується модель пружних сфер (рис.1) [8].
            Сили, які що діють на частку, можуть бути описані залежно від поведінки матеріалу частки під час зіткнення. Сила взаємодії ділиться на нормальну (рів. 5, 6, 8) і тангенціальну складову (рів. 10, 12). Нормальна сила ділиться на еластичну і розсіюючу частину.

(5)

де k та еластична і розсіююча константи. s — перетин у напрямі нормалі. Еластична частина нормальної сили, представлена Герцем [1] і розсіююча частина, представлена Брілліантовим [6] приведені у рів. 6:

(6)

де E* ефективний модуль Юнга часток (індекс i та j), R* — эфективний радіус, n — коефіцієнт Пуассона, Ad — функція в'язкості матеріалу:

(7)

h — розсіюючий коефіцієнт часток, що стикаються. E — модуль Юнга частки.
У рів. (6-7) E_i = E_j = E*, n_i = n_j.
Нелінійна модель нормальної сили була представлена Кувабара і Коно [3]:

(8)

Лінійна модель нормальної сили була представлена Уолтоном і Брауном [7]:

(9)

де l, u — індекси завантаженого і розвантаженого стану часток k_l, k_u — жорсткість пружини під час завантаження і розвантаження. s₀ — максимальна результуюча деформація взаємодіючих часток.
Модель тангенціальної сили була представлена Хаффом і Вернером [1]:

(10)

де — відносна швидкість центрів сфер (рів. 11). — коефіцієнти розсіювання для нормальної і тангенціальної сили, m — коефіцієнт тертя.

(11)

Лінійна модель тангенціальної сили була також представлена Ді Майо і Ді Ренцо [2]:

(12)

де k^t — тангенціальна жорсткість. s^t — зсув в тангенціальному напрямі:

(13)

            Найкраще співвідношення з експериментальними даними показала розширена лінійна модель нормальної сили представлена Уолтоном і Брауном [3]. Більш того, використання лінійної моделі прискорює моделювання в порівнянні з нелінійними моделями. Лінійна тангенціальна модель представлена Ді Майо і Ді Ренцо [2] є однією з найбільш відповідних експериментальним даним.

            Інтегрування рівнянь руху Ньютона може бути виконане за допомогою схеми інтегрування Gear. Алгоритм Gear (рис. 2) підходить для вирішення даної проблеми, в основному через його чисельну стабільність [1].

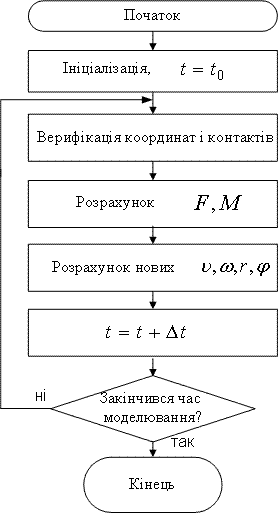Рисунок 2 — схема интегрирования Gear

Першим кроком (у циклі) в алгоритмі передбачаються позиції часток, швидкості, і похідні по часу t+Δt використовуючи розкладання у ряд Тейлора (рів. 14).

		(14)

Після чого передбачені координати і похідні використовуються для розрахунку і . З сил і моментів обчислюються лінійні і кутові прискорення і (рів. 15). Щоб прискорити обчислення був розроблений алгоритм фіксації колізій заснований на Verlet списках.

(15)

            У цьому алгоритмі сили розраховуються між частинками, які є близькими сусідами, тобто дистанція між ними менша за verlet дистанцію (рів. 16)

< verlet дистанція

(16)

            Verlet список складається для кожної частки і містить індекси сусідніх часток. Подвійне включення у список Verlet виключається, використовуючи обмеження, що частинка з індексом i має тільки сусідів з індексом j < i. Список необхідно складати спочатку у випадку, якщо частка пересунулася на відстань, яка дорівнює половині verlet дистанції.
             Простір моделювання ділиться сіткою на осередки. Розмір кожного осередку не повинен перевищувати розміру найбільшої частки. Умова (рів. 16) перевіряється тільки для часток у сусідніх осередках.
            В случае если частицы движутся по направлению друг к другу с максимальной скоростью, они могут столкнуться не присутствуя в списке Verlet. Таким образом необходимо сохранять коордиднаты частиц и списки сосдей когда составляется новый список Verlet. В худшем случае моделирование должно быть возвращено к шагу, где был составлен последний удачный список и продолжить с увеличенной Verlet дистанцией.
            У випадку якщо частки рухаються по напряму один до одного з максимальною швидкістю, вони можуть зіткнутися у той момент коли вони не присутні у списку Verlet. Таким чином необхідно зберігати коордиднати часток і списки сусідів коли складається новий список Verlet. У гіршому разі моделювання повинне бути повернене до кроку, де був складений останній вдалий список і продовжити із збільшеною Verlet дистанцією.
            На додаток до алгоритмів оптимізації може бути використане розпаралелювання для прискорення обчислень.

            Розробка стратегії розпаралелювання грає важливу роль, оскільки необхідно моделювати великі кількості часток. Для цього об'єм моделювання розбивається на мережу пересічених осередків. Після чого розрахунки розпаралелюються з урахуванням розбиття об'єму моделювання. Всі частки в осередку або в групі осередків розраховуються незалежно на окремому процесорі.
            Ефективність стратегії розпаралелювання залежить від мінімізації двох основних критеріїв: дисбалансу завантаження і об'єму передаваних даних. Мінімізуючи дисбаланс завантаження, розрахунки повинні бути рівномірно розподілені між процесорами. Це може бути досягнуто за допомогою не постійного розміру сітки, де розмір осередку пропорційний кількості часток в осередку (рис. 4). Мінімізація об'єму передаваних даних між процесорами може бути досягнута використовуючи сітку з рухомими межами. Міграція часток між процесорами може бути мінімізована, якщо сітка рухається в тому ж напрямі, що і потік часток.
            Основна частина комп'ютерного часу в моделюванні сипких матеріалів витрачається на векторні операції. Використання SSE (Streaming SIMD Extensions) інструкцій може зробити розрахунки з векторами і матрицями до 4х разів швидше.

            На рис.4 представлені процеси заповнення і звільнення закритого бункера у двовимірному і тривимірному просторі. На третьому малюнку зліва представлена зворотна хвиля від удару часток о дно бункеру. На четвертому малюнку представлені періодичні межі об'єму моделювання, тобто частк, що випали з бункера, вкидаються назад в нього з новою початковою швидкістю. Стінки бункера зроблені з таких самих часток, але статичних.

Рисунок 4 — DEM- моделювання заповнення і звільнення бункера у 2D і 3D
Параметри анімації: кількість кадрів: 6; кількість циклів: 7; Розмір: 39 Кб; Зроблено у AVI->GIF Converter & GIF-Animator

            Моделювання сипких матеріалів на мікро-рівні дає можливість передбачити їх макро-поведінку, аналізувати вплив різних параметрів процесів і розробляти стратегії контролю. Модель пружних сфер, розроблена у DEM моделюванні, описує зіткнення між частками оптімальніше, ніж модель твердих сфер.
            Одночасно з алгоритмом Gear оптимізація розрахунків може бути виконана за допомогою Verlet списків. Додатково розроблена стратегія розпаралелювання може дати добрий фактор прискорення і може бути ефективно використана у мережах стандартних комп'ютерів.

            1. T. Poeschel, T. Schwager. Computational granular dynamics. Models and algorithms. Springer, 2005.
            2. H. Kruggel-Emden, S. Wirtz, V. Scherer. A study on tangentional force laws applicable to the discrete element method for materials with viscoelastic or plastic behaviour, Chemical Engineering Science 63, 2008, 1523-1541.
            3. H. Kruggel-Emden, E. Simsek, S. Rickelt, S. Wirtz, V. Scherer. Review and extension of normal force models for DEM, Powder Technology 130, 2007, 157-173.
            4. S. Antonyuk, M. Khanal, J. Tomas, S. Heinrich and L. Moerl. Impact breakage of spherical granules: experimental study and DEM simulation, Chemical Engineering and Processing 45, 2006, 838-856.
            5. P.A. Cundall, O.D.L. Strack. A discrete numerical model for granular assemblies. Geotechnique 29, 1979, 47-65.
            6. N.V. Brilliantov, F. Spahn, J.-M. Hertzsch, T. Poeschel. Model for collision in granular gases, Physical review E, Vol. 53, 1996.
            7. Walton, O.R., Braun, R.L. Viscosity, granular-temperature, and stress calculations for shearing assemblies of inelastic, frictional disks. Journal of Rheology, 30, 1986, 949- 980.
            8. Antonyuk, S., Palis, S., Heinrich, S. Breakage behaviour of agglomerates and crystals by static loading and impact, Powder Technology, Special Issue: Agglomeration, in Press, February 2010.
            9. Poschel, T., Saluena, C., Schwager, T., 2001. Scaling properties of granular materials. Physical Review E 64 (1), (Art. No. 011308 Part 1).
            10. Schaefer, J., Dippel, S., Wolf, D.E., 1996. Force schemes in simulations of granular materials. Journal De Physique I 6 (1), 5–20.

---

            При написанні цього автореферату магістерська робота ще не завершена.
Остаточне завершення: грудень 2010 р. Повний текст роботи і матеріали по темі можуть бути отриманий у автора або його керівника після вказаної дати.