Реферат
Содержание
Введение
Актуальность темы
Научная значимость работы
Практическая ценность результатов работы
Объект и предмет исследований
Обзор исследований по теме
Обнаружение точек, линий, перепадов
Операторы градиента
Лапласиан
Связывание контуров и нахождение границ с помощью локальной обработки
Пороговая обработка
Обработка с глобальным порогом
Выращивание областей
Сегментация по морфологическим водоразделам
Построение перегородок
Алгоритм сегментации по водоразделам
Использование маркеров
Использование движения при сегментации. Пространственные методы
Заключение
Список литературы
Исследование методов сегментации изображений
Введение
Сегментация подразделяет изображение на составляющие
его области или объекты. Та степень детализации, до
которой доводится такое разделение, зависит от решаемой задачи.
Сегментацию следует прекратить, когда интересующие объекты изолированы.
Не имеет смысла проводить сегментацию меньше того уровня детализации,
который необходим для обнаружения подобных дефектов.
Сегментация изображений, не являющихся тривиальными,
представляет собой одну из самых сложных задач обработки изображений.
Конечный успех компьютерных процедур анализа изображений во многом
определяется точностью сегментации, по этой причине значительное
внимание должно быть уделено повышению её надёжности.
Актуальность темы
Задача сегментации очень актуальна, поскольку с её помощью можно независимо
обрабатывать объекты видеопоследовательности. Это позволяет акцентировать внимание на
существенных деталях и пренебрегать качеством несущественных (напр. фона).
Научная значимость работы
Научная значимость данной работы заключается в разработке улучшенного метода сегментации кадров видеопоследовательности.
Практическая ценность результатов работы
В ходе выполнения работы после проведения моделирования с улучшенным методом сегментации
предполагается получить более оптимальное расслоение ключевого кадра для формирования последующих промежуточных
кадров.
Объект и предмет исследований
Объектом исследований является изображение, кадр видеопоследовательности, содержащее различные характерные фрагменты.
Предметом исследований является метод расслоения изображения на составляющие части.
Обзор исследований по теме
Тематика сегментации изображений встречается в работах магистрантов и сотрудников ДонНТУ. В большинстве работ
сегментация используется для медицинских целей, для задач автоматизации технического контроля и, как
предварительный шаг, для распознавания объектов. Также присутствуют работы по кластеризации, поиску
определённых объектов в видеоинформации. Найти работы можно с помощью раздела «Ссылки».
В целом работ по сегментации изображений представлено большое количество. Зачастую разрабатываются
алгоритмы для решения какой-то конкретной задачи, т.е. известна определённая априорная информация.
Часто используют методы, в основе которых лежит метод сегментации по водоразделам.
Основные результаты
Обнаружение точек, линий, перепадов
Алгоритмы сегментации изображений основываются на
одном из двух базовых свойств сигнала яркости: разрывности и
однородности. Рассмотрим три основных вида разрывов яркости: точек,
линий, перепадов. Наиболее общий способ поиска – использование
скользящей маски.
 (1.1)
(1.1)
Обнаружение отдельных изолированных
точек на изображении не представляет сложности. К примеру, воспользуемся
маской размером 3х3:
| -1 |
-1 |
-1 |
| -1 |
8 |
-1 |
| -1 |
-1 |
-1 |
Рисунок 1.1 – Общее представление маски размерами 3х3
В том пикселе, куда попадает центр маски, обнаружена точка, если
 (1.2)
(1.2)
где Т – неотрицательный порог, |R| –
сумма вычисленная по формуле (1.1). В данной формуле измеряется
взвешенная сумма разностей значений центрального элемента и его
соседей. Идея в том, что изолированная точка будет заметно отличаться по
яркости от ближайших соседей. Также сумма коэффициентов маски равна
нулю, так что на областях постоянной яркости она будет давать нулевой
отклик.
Для обнаружения линий используются маски вида:
|
|
|
|
|
| Горизонтальная |
+45 |
Вертикальная |
-45 |
Рисунок 1.2 – Маски для обнаружения линий
Наиболее сильный отклик будут давать
линии толщиной в один пиксель: горизонтальные; под углом +45
градусов; вертикальные; под углом -45градусов. Суммы коэффициентов
маски равны нулю. Аналогично можно создавать маски поиска линий, толщина
которых больше одного пикселя. Для поиска линий, располагающихся под
углами отличными от 45 и 90 градусов, необходимо использовать маски
большего размера и учитывать «сглаживание» таких линий на квадратных
матрицах.
Обнаружение перепадов яркости
является намного более общим подходом к нахождению интерпретируемых
разрывов на яркостной картине. Примеры идеального и наклонного
перепадов:
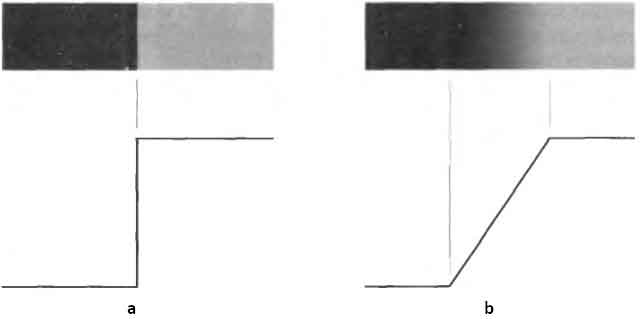
Рисунок 1.3 – (a) Модель идеального перепада яркости. (b) Модель наклонного перепада яркости
Область перепада зависит от качества
системы регистрации, шага дискретизации, освещения. На рисунке 1.4 приведён
горизонтальный профиль перепада яркости, его первая и вторая
производные. Первая производная имеет постоянное ненулевое значение на
участке перепада, и нулевое значение при постоянном уровне яркости.
Вторая производная положительна в точке перехода от тёмного участка к
наклонному, отрицательна в точке перехода от наклонного участка к
светлому, и равна нулю на линейном склоне и участках постоянной яркости.
Можно прийти к выводу, что по первой производной можно обнаружить
перепад яркости в каждой точки изображения. По знаку второй производной
определяют, лежит ли пиксель в тёмной либо светлой части перепада.
Свойства второй производной вблизи перепада яркости: 1) два ненулевых
(положительное и отрицательное) значения для каждого перепада, что
является нежелательным свойством; 2) воображаемая прямая линия,
соединяющая максимальные положительные и отрицательные значения второй
производной, пересекает нулевой уровень приблизительно в середине
перепада яркости.
Свойство пересечения нулевого уровня второй производной полезно для
локализации середины широких перепадов.
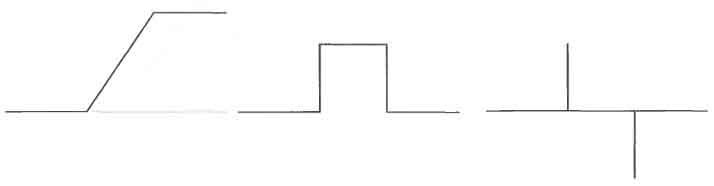
Рисунок 1.4 – Горизонтальный профиль яркости, первая и вторая производные
В реальных изображениях в областях с
перепадами яркости также будет присутствовать шум.
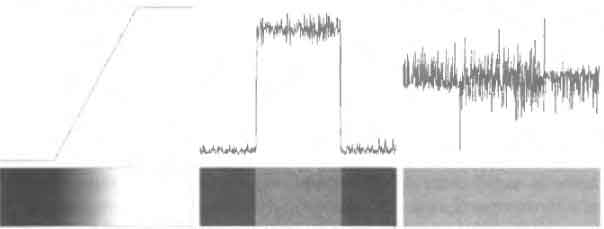
Рисунок 1.5 – Присутствие шума в профиле яркости и его влияние на первую и вторую производные
При большом количестве шумов будет тяжело распознать перепад яркости в
первой производной. Вторая производная ещё более чувствительна к
перепадам яркости. Поэтому в практических задачах целесообразно
сглаживать изображение перед вычислением производных.
Операторы градиента
Градиент изображения f(x, y) в точке (x, y) – это вектор:
 (1.3)
(1.3)
Модуль вектора:
 (1.4)
(1.4)
Величина равна максимальной скорости изменения функции.
Направление вектора градиента:
 (1.5)
(1.5)
Вычисление градиента изображения
состоит в получении величин частных производных df/dx и df/dy для каждой
точки. Первые частные производные можно найти с помощью:
а) перекрёстного градиента оператора Робертса: Gx = (z9-z5);
Gy = (z8 – z6);
б) оператора Превитта: Gx = (z7+z8+z9) – (z1 + z2 + z3);
Gy = (z3+z6+z9) – (z1 + z4 + z7);
в)оператора Собела: Gx = (z7+2*z8+z9) – (z1 + 2*z2 + z3);
Gy = (z3+2*z6+z9) – (z1 + 2*z4 + z7).
| z1 |
z2 |
z3 |
| z4 |
z5 |
z6 |
| z7 |
z8 |
z9 |
|
|
|
| Окрестность |
Маски оператора Робертса |
|
|
|
|
|
| Маски оператора Превитта |
Маски оператора Собела |
Рисунок 1.6 - Окрестность 3х3 внутри изображения и различные маски, применяемые
для вычисления градиента в центральной точке окрестности
Оператор Робертса неудобен, т.к. нет
чётко выраженного центрального пикселя. Маски оператора Собела лучше
масок Превитта тем, что уменьшается эффект сглаживания за счёт придания
средним точкам больше веса. Также маски Превитта и Собела можно изменить
таким образом, чтобы они давали максимальный отклик для контуров,
направленных диагонально.
Для упрощения вычисления модуля градиента используют формулу:
 (1.6)
(1.6)
Лапласиан
Лапласиан двумерной функции f(x, y)
представляет собой производную второго порядка, определяемую выражением:
 (1.7)
(1.7)
Применительно к окрестностям 3х3 используют выражение:
 (1.8)
(1.8)
Дискретное приближение с
использованием диагональных соседних элементов имеет вид:
 (1.9)
(1.9)
|
|
| -1 |
-1 |
-1 |
| -1 |
8 |
-1 |
| -1 |
-1 |
-1 |
|
Рисунок 1.7 – Маски лапласиана, для реализации формул (1.8) и (1.9)
Связывание контуров и нахождение границ с помощью локальной обработки
Анализируется небольшая окрестность
(3х3 или 5х5) каждой точки (x, y) изображения, которая отмечена как
контурная. Все точки, сходные по определённым критериям, связываются и
образуют контур. Используют величину отклика и направление вектора
градиента.
 (1.10)
(1.10)
где Е – заданный неотрицательный порог (по модулю градиента).
 (1.11)
(1.11)
где А – заданный неотрицательный
угловой порог. Направление контура в точке (x, y) перпендикулярно
направлению вектора градиента в этой точке.
Пиксель в окрестности объединяется с центральным, если критерии
сходятся. Процесс повторяется для каждой точки с одновременным
запоминанием найденных пикселей.
Также для связывания контуров используют глобальный анализ с помощью
преобразований Хафа и методов теории графов.
Пороговая обработка
К примеру, изображение содержит
светлые объекты на тёмном фоне, так что яркости пикселей объекта и фона
сосредоточены вблизи двух преобладающих значений. Очевидный способ –
задать значение порога T. Тогда любая точка (x, y), в которой f(x, y)>T,
называется точкой объекта, а в противном случае – точкой фона.
Более обобщённый вариант содержит объекты двух видов и фон. У
многоуровневого порогового преобразования используются несколько порогов
яркости, каждый пиксель проверяется на принадлежность диапазону.
Пороговое преобразование может рассматриваться как операция, при которой
производится сравнение с функцией T:
T=T(x,y,p(x,y),f)
(1.12)
где f – изображение, а p(x,y) обозначает некоторую локальную
характеристику точки (x,y) изображения, например, среднюю яркость в
окрестности с центром в этой точке. Изображение g(x,y), получаемое в
результате порогового преобразования, определяется следующим образом:
 (1.13)
(1.13)
1 – объект, 2 – фон. Если T зависит только от f, то порог глобальный. Если
T зависит и от координат x и y, то порог локальный или динамический.
Если T зависит от p(x,y), то порог адаптивный.
Обработка с глобальным порогом
Это сегментация с помощью глобального порога T. Успешность метода зависит от того,
насколько хорошо гистограмма поддаётся разделению. Порог – среднее между минимальным
и максимальным значением яркости. Применяется в задачах технического контроля, где
обычно можно управлять условиями освещения.
Алгоритм выбора порога T:
1. Выбирается некая начальная оценка порога T.
2. Проводится сегментация изображения с помощью порога T. В результате образуются
две группы пикселей: G1, состоящая из пикселей с яркостью больше T, и G2,
состоящая из пикселей меньшей или равной T.
3. Вычисляются значения µ1 и µ2 средних яркостей пикселей по областям G1 и G2 соответственно.
4. Вычисляется новое значение порога: T = (µ1 + µ2)/2.
5. Повторяются шаги со 2 по 4 до тех пор, пока разница значений T при
соседних итерациях не окажется меньше значения наперёд заданного параметра T0.
Если есть основания полагать, что объект и фон занимают сравнимые площади
в изображении, хорошим начальным порогом T будет средний уровень яркости изображения.
Если занимаемая объектом площадь мала по сравнению с площадью фона (или наоборот),
то подходящим начальным порогом будет полусумма минимального и максимального значений яркости.
Выращивание областей
Выращивание областей – это процедура, которая группирует пиксели или подобласти в более
крупные области по заранее заданным критериям. Вначале берётся множество точек, являющимися
«центрами кристаллизации», а затем на них наращиваются области путём присоединения к каждому
центру тех пикселей из числа соседей, которые по своим свойствам близки к центру кристаллизации.
Начальные точки выбираются на основании сути задачи. При отсутствии априорной информации процедура
состоит в вычислении одного и того же набора свойств для каждого пикселя.
Выбор критериев сходства зависит не только от выбираемой задачи, но и от вида данных (цветное
– монохромное).
Существует проблема остановки процесса выращивания областей. По идее, необходимо остановить процесс,
когда отсутствуют пиксели, удовлетворяющие критериям. Мощность алгоритма можно повысить за
счёт привлечения дополнительных критериев, например, размеры и форма выращиваемой области.
Для этого необходима хотя бы грубая модель ожидаемых результатов.
Сегментация по морфологическим водоразделам
До сих пор обсуждались способы сегментации, основанные на трёх главных подходах:
(а) обнаружение разрывов, (б) пороговой обработке, (в) обработке областей.
Сегментация по водоразделам заключает в себе многие концепции трёх рассмотренных подходов.
Понятие водораздела основано на представлении изображения как трёхмерной поверхности,
с двумя пространственными координатами и уровнем яркости. В такой интерпретации
рассматриваются точки 3-х видов: (а) точки локального минимума; (б) точки, находящиеся
на склоне, т.е. с которых вода стекает в один локальный минимум; (в) точки, находящиеся
на пике, с которых вода стекает более чем в один локальный минимум. Для каждого лок.
минимума точки условия (б) называются бассейном или водосбором. Точки условия (в) – линии водораздела.
Главная цель – нахождение линий водораздела. Основная идея. В локальных минимумах проколоты отверстия и снизу подступает вода. Когда вода в двух соседних бассейнах будет близка к тому, чтобы слиться, ставится перегородка. По мере наполнения водой останутся видны только перегородки.
На практике метод сегментации по водоразделам часто применяется не к самому изображению, а к его градиенту. Локальный минимум – малое значение градиента.
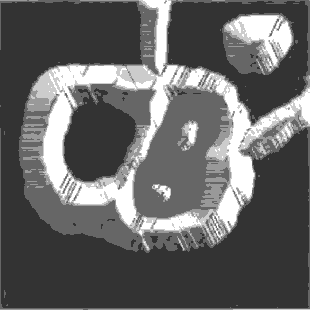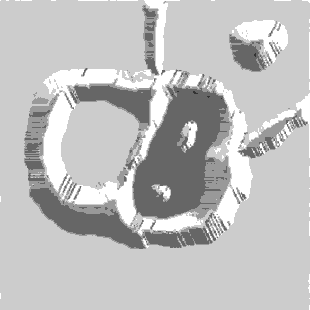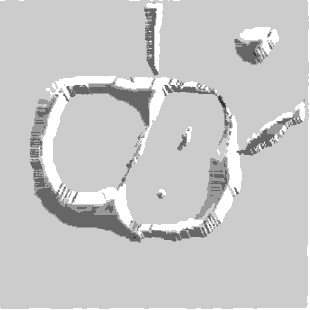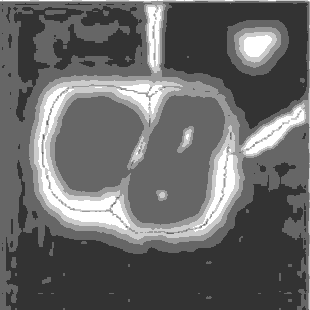
Рисунок 1.8 – Сегментация изображения по морфологическим водоразделам
(Анимация состоит из 7 кадров, 40Кб с задержкой в 0.3 с между кадрами;
задержка до повторного воспроизведения составляет 1с; количество циклов воспроизведения
– 10)
Построение перегородок
Построение перегородок основано на двоичных изображениях, которые являются подмножествами двумерного целочисленного пространства. Простейший способ построения линий раздела для множеств, образованных двоичными точками, состоит в использовании морфологической дилатации.
Обозначим через М1 и М2 множества точек, соответствующие локальным минимумам двух рассматриваемых бассейнов. Через Cn-1(M1) и Cn-1(M2) обозначим множества точек, покрытых водой в этих бассейнах на (n-1) шаге заполнения.
Имеется два бассейна – две компоненты связности (пусть C[n-1] объединение точек этих множеств). По мере заполнения бассейна образуется одна компонента связности. Две компоненты связности превратились в одну, указывает на то, что произошло слияние. q – единая связная компонента. Необходимо отметить, что можно выделить из q две компоненты
связности шага n-1: q  C[n-1]. C[n-1].
К компонентам связности применяется операция дилатации с условиями: (1) применение дилатации должно ограничиваться множеством q; (2) дилатация не должна выполняться в тех точках, где это приведёт к слиянию обрабатываемых множеств, так что они станут единой связной компонентой.
Обычно высота всех перегородок принимается равной максимально возможному уровню яркости, плюс единица. Важно отметить, что перегородки, построенные с применением данной процедуры и являющиеся искомыми границами сегментации, представляют собой связные компоненты. То есть метод исключает появление разрывов в линиях сегментации.
Алгоритм сегментации по водоразделам
Пусть М1, М2, … , MR – множества точек, которые соответствуют локальным минимумам поверхности g(x,y)
(градиент изображения). C(Mi) – множество точек Mi локального минимума. min и max – наименьшие
и наибольшие значения изображения g(s, t). T[n] означает множество точек (s, t), для которых g(s, t)
< n, т.е.
T[n] = {(s, t) | g(s, t) < n}.
(1.14)
T[n] – множество точек, в которых поверхность g(x, y) лежит ниже g(x, y) = n.
При заполнении водой уровень поднимается в виде целочисленных дискретных приращений от n =min + 1 до n = max +1. Необходимо на каждом шаге знать число точек, лежащих ниже уровня воды. Вообразим, что все точки T[n] (ниже уровня n) отмечены чёрным, а остальные белым.
Пусть Cn(Mi) обозначает множество точек бассейна с локальным минимумом Mi, которые залиты водой на шаге n. Cn(Mi) можно рассматривать как двоичное изображение, задаваемое
Cn(Mi) = C(Mi)  T[n].
(1.15) T[n].
(1.15)
Другими словами Cn(Mi) = 1 в тех точках (x, y), для которых одновременно выполняется (x, y)  C(Mi) и (x, y) C(Mi) и (x, y)  T[n], в остальных точках изображения Cn(Mi) = 0. T[n], в остальных точках изображения Cn(Mi) = 0.
Пусть C[n] – объединение залитых водой частей всех бассейнов на шаге n:
C[n] =  Cn(Mi).
(1.16) Cn(Mi).
(1.16)
Тогда C[max + 1] есть объединение всех имеющихся бассейнов:
C[max + 1] =  C(Mi).
(1.17) C(Mi).
(1.17)
В алгоритме не происходит удаление элементов из множеств Cn(Mi) и T[n]. Следовательно, C[n-1] является подмножеством C[n]. Также C[n] является подмножеством T[n], а значит и C[n-1] подмножество T[n]. Следует результат: каждая компонента связности множества C[n-1] содержится ровно в одной связной компоненте множества T[n].
Алгоритм нахождения линий водораздела начинается с инициализации C[min + 1] = T[min + 1]. После этого алгоритм выполняется рекуррентно, предполагая на n-ом шаге множество C[n-1] уже построенным. Для получения C[n] из C[n-1] применяется процедура. Пусть Q[n] – множество компонент связности T[n]. Тогда для каждой связной компоненты q  Q[n] есть три возможности: Q[n] есть три возможности:
а) q  C[n-1] – пустое множество; C[n-1] – пустое множество;
б) q  C[n-1] содержит единственную компоненту связности множества C[n-1]; C[n-1] содержит единственную компоненту связности множества C[n-1];
в) q  C[n-1] содержит более одной компоненты связности множества C[n-1]. C[n-1] содержит более одной компоненты связности множества C[n-1].
Способ построения C[n] по C[n-1] зависит от того, какое из этих трёх условий имеет место. Условие (а) означает, что встретился новый локальный минимум (начинается наполнение нового бассейна); в этом случае для построения множества C[n] компонента q добавляется к C[n-1]. Условие (б) имеет место, когда q лежит внутри бассейна некоторого локального минимума; в этом случае для построения множества C[n] компонента q также добавляется к C[n-1]. Условие (в) возникает, когда встретились точки гребня, разделяющие два или более бассейна. Необходимо построить перегородку (или перегородки). Перегородка толщиной в один пиксель строится, применяя к множеству q  C[n-1] операцию дилатации по примитиву 3x3, заполненную единицами, и затем ограничивая результат дилатации точками множества q. C[n-1] операцию дилатации по примитиву 3x3, заполненную единицами, и затем ограничивая результат дилатации точками множества q.
Эффективность алгоритма можно повысить, используя только те значения n, которые соответствуют уровням яркости, встречающимся в g(x, y). Значения определяются по гистограмме.
Использование маркеров
Алгоритм сегментации по водоразделам обычно приводит к избыточной сегментации, вызванной шумом и другими локальными неровностями на градиентном изображении. Необходимо выполнить предварительную процедуру обработки, основанную на идее маркеров.
Маркер представляет собой связную компоненту, принадлежащую изображению. Внутренние маркеры относятся к интересующим объектам, внешние маркеры соответствуют фону. Процедура выбора маркера: (1) предобработка, и (2) выработка критериев, которым должны удовлетворять маркеры. Для снижения влияния мелких деталей является фильтрация с помощью сглаживающего фильтра.
Пусть внутренний маркер определяется как область, (1) окружённая точками с большей «высотой»; (2) такая, что её точки образуют компоненту связности; и (3) все точки которой имеют одинаковые значения яркости. Внутренние маркеры, найденные на сглаженном изображении согласно такому определению, показаны в виде светло-серых пятен:
Затем к сглаженному изображению применяется метод сегментации по водоразделам, с тем ограничением, что в качестве локальных минимумов рассматриваются только внутренние маркеры. Полученные в результате линии водоразделов, являются внешними маркерами. Внешние маркеры эффективно разграничивают изображение на области, каждая из которых содержит единственный внутренний маркер и часть фона. После этого задача сводится к разделению каждой такой области на объект и фон. Такую упрощённую задачу можно решать многими методами. Можно применить тот же алгоритм сегментации по водоразделам применительно к каждой области.
Маркер может основываться как на связности и значениях яркости, так и на размерах, форме, текстуре. В сегментации очень важными являются априорные знания.
Использование движения при сегментации. Пространственные методы
Один из простейших подходов к обнаружению изменений, произошедших между двумя кадрами f(x, y, ti) и f(x, y, tj), состоит в поэлементном сравнении этих двух элементов. Один из способов сравнение – построение разностного изображения, где неподвижные составляющие взаимно уничтожаются.
Разностное изображение можно определить:
 (1.18)
(1.18)
где Т – заданный порог. dij(x, y) принимает значение 1 в точке с пространственными координатами (x, y) только в том случае, если значения яркости существенно отличаются.
При обработке динамических изображений, все единичные пиксели считаются результатом движения объекта. Подход применим, если изображения пространственно совмещены, и если флуктуации яркости не выходят за границы значения Т. На практике ненулевые элементы часто являются следствием шума. Поскольку они образуют небольшие изолированные группы точек, то они удаляются путём нахождения 4- или 8-ми связанных областей единичных пикселей. Хотя это может привести к пропуску малых и/или медленно движущихся объектов.
Для уменьшения вероятности пропуска движения малых объектов из-за шумов необходимо рассматривать последовательность кадров, чтобы игнорировать изменения, встречающиеся изредка.
Последовательность кадров f(x, y, ti), f(x, y, t2), … , f(x, y, tn) и f(x, y, ti) – опорный кадр. Накопленное разностное изображение (НРИ) формируется путём сравнения опорного изображения с каждым следующим кадром. Для каждого пикселя ведётся счётчик, который накапливает значение, если есть отличие между опорным и текущим кадром.
Рассматривают абсолютные, положительные и отрицательные НРИ. Опорное изображение R(x, y) и пусть k обозначает момент времени tk, т.е. f(x, y, k) = f(x, y, tk). Полагаем также R(x, y)= f(x, y, 1). Тогда для любого k>1 определяется:
 (1.19)
(1.19)
 (1.20)
(1.20)
 (1.21)
(1.21)
Начальные значения счётчиков нулевые, размеры НРИ совпадают с размерами исходного изображения.

Рисунок 1.9 – Накопленные разностные изображения прямоугольного объекта:
абсолютное, положительное и отрицательное НРИ
На практике не всегда можно получить опорное изображение, состоящее только из неподвижных
объектов. Его приходится строить на основании набора изображений, содержащее один или более движущихся объектов.
Заключение
Из приведенного выше материала видно, что существует большое количество методов сегментации изображений.
Хотя набор методов не исчерпывающий, они являются характерными представителями техники сегментации. Также можно
прийти к выводу, что различные техники можно совмещать. К примеру, есть возможность совместить пространственную сегментацию
с сегментацией движущихся объектов.
Список литературы
-
Гонсалес Р. Цифровая обработка изображений / Гонсалес Р., Вудс Р.; пер. с англ. П. А. Чочиа
– Москва: Техносфера, 2005, С. 812-916.
-
Segmentation (image processing) [Электронный ресурс] –
Режим доступа к статье:
http://en.wikipedia.org/wiki/Segmentation_(image_processing)
-
Универсальная классификация алгоритмов сегментации изображений [Электронный ресурс]
/ С.В. Поршнев, А.О. Левашкина – Режим доступа к статье:
http://www.jurnal.org/articles/2008/inf23.html
-
D.J.Williams and M.Shas. “Edge Contours Using Multiple Scales”.
Computer Vision, Graphics and Image Processing, 1990,
pp.256-274.
-
V. Lacroix. “The Primary Raster: A Multiresolution Image
Description”. In Proceedings of the 10th International Conference on
Pattern Recognition, 1990, pp. 903-907.
-
J.F.Canny. “A Computational Approach to Edge Detection”. IEEE
Transactions on Pattern Analysis and Machine Intelligence,
1986, pp. 679-698.
-
D. Ziou and S. Tabbone. “A Multi-Scale Edge Detector”. Pattern
Recognition, 1993, pp.1305-1314.
-
T. Lindeberg. “Edge Detection and Ridge Detection with Automatic
Scale Selection”. In Proceedings of IEEE, International Conference
on Computer Vision and Pattern Recognition, San Francisco, 1996, pp.
465-470.
-
William K. Pratt Digital Image Processing,
Wiley-Interscience Publication, 2001, pp. 551-589.
-
L. M. J. Florack, B. M. ter Haar Romeny, J. J. Koenderink, and M. A.
Viergever. “Scale and the diferential structure of images”. Image
and Vision Computing, 1992, pp.376-388.
|

