Реферат
Зміст
Вступ
Актуальність теми
Наукова значимість роботи
Практична цінність результатів роботи
Об'єкт і предмет досліджень
Огляд досліджень за темою
Виявлення точок, ліній, перепадів
Оператори градієнта
Лапласіан
Зв'язування контурів і знаходження меж з допомогою локального опрацювання
Порогове опрацювання
Опрацювання з глобальним порогом
Вирощування областей
Сегментація за морфологічними вододілами
Побудова перегородок
Алгоритм сегментації за вододілами
Використання маркерів
Використання руху при сегментації. Просторові методи
Висновок
Список літератури
Дослідження методів сегментації зображень
Вступ
Сегментація підрозділяє зображення на складові його області або об'єкти.
Та ступінь деталізації, до якої доводиться такий поділ, залежить від
розв'язуваної задачі. Сегментацію слід припинити, коли необхідні об'єкти
ізольовані. Не має сенсу проводити сегментацію менше того рівня
деталізації, який необхідний для виявлення подібних дефектів.
Сегментація зображень, які не є тривіальними, – це одна з
найскладніших задач опрацювання зображень. Кінцевий успіх комп'ютерних
процедур аналізу зображень багато в чому визначається точністю
сегментації, з цієї причини значна увага має бути приділена підвищенню
її надійності.
Актуальність теми
Завдання сегментації дуже актуальне, оскільки з її допомогою можна
незалежно обробляти об'єкти відеопослідовності. Це дозволяє акцентувати
увагу на істотних деталях і нехтувати якістю несуттєвих (напр. фону).
Наукова значимість роботи
Наукова значимість даної роботи полягає у розробці поліпшеного методу
сегментації кадрів відеопослідовності.
Практична цінність результатів роботи
У ході виконання роботи після проведення моделювання з поліпшеним
методом сегментації передбачається одержати більш оптимальне
розшарування ключового кадру для формування наступних проміжних кадрів.
Об'єкт і предмет досліджень
Об'єктом досліджень є зображення, кадр відеопослідовності, що містить
різні характерні фрагменти. Предметом досліджень є метод розподілення по шарах
зображення на складові частини.
Огляд досліджень за темою
Тематика сегментації зображень зустрічається в роботах магістрантів і
співробітників ДонНТУ. У більшості робіт сегментація використовується
для медичних цілей, для задач автоматизації технічного контролю і, як
попередній крок, для розпізнавання об'єктів. Також присутні роботи по
кластерізації, пошуку певних об'єктів в відеоінформації. Знайти роботи
можна за допомогою розділу посилань.
У цілому робіт з сегментації зображень представлена велика кількість.
Найчастіше розробляються алгоритми для вирішення якоїсь конкретної
задачі, тобто відома певна апріорна інформація. Часто використовують
методи, в основі яких лежить метод сегментації по вододілах.
Основні результати
Виявлення точок, ліній, перепадів
Алгоритми сегментації зображень ґрунтуються на одній з двох базових
властивостей сигналу яскравості: розривності та однорідності. Розглянемо
три основних види розривів яскравості: точок, ліній, перепадів. Найбільш
загальний спосіб пошуку – використання ковзної маски.
 (1.1)
(1.1)
Виявлення окремих ізольованих точок на зображенні не представляє
складності. Скористаємося маскою розміром 3х3:
| -1 |
-1 |
-1 |
| -1 |
8 |
-1 |
| -1 |
-1 |
-1 |
Рисунок 1.1 – Загальне подання маски розмірами
3х3
У тому пікселі, куди потрапляє центр маски, виявлена точка, якщо
 (1.2)
(1.2)
де Т – невід'ємні поріг, |R| – сума обчислена за формулою (1.1). У цій
формулі вимірюється зважена сума різниць значень центрального елемента
та його сусідів. Ідея в тому, що ізольована точка буде помітно
відрізнятися за яскравістю від найближчих сусідів. Також сума
коефіцієнтів маски дорівнює нулю, так що на областях постійної
яскравості вона буде давати нульової відгук.
Для виявлення ліній використовуються маски виду:
|
|
|
|
|
| Горизонтальна |
+45 |
Вертикальна |
-45 |
Рисунок 1.2 – Маски для виявлення ліній
Найбільш сильний відгук будуть давати лінії товщиною в один піксель:
горизонтальні; під кутом +45 градусів; вертикальні; під
кутом -45градусов. Суми коефіцієнтів маски дорівнюють нулю. Аналогічно
можна створювати маски пошуку ліній, товщина яких більше одного пікселя.
Для пошуку ліній, розташованих під кутами відмінними від 45 і 90
градусів, необхідно використовувати маски більшого розміру і враховувати
«згладжування» таких ліній на квадратних матрицях.
Виявлення перепадів яскравості є набагато більш загальним підходом до
знаходження розривів на зображені. Приклади
ідеального і похилого перепадів:
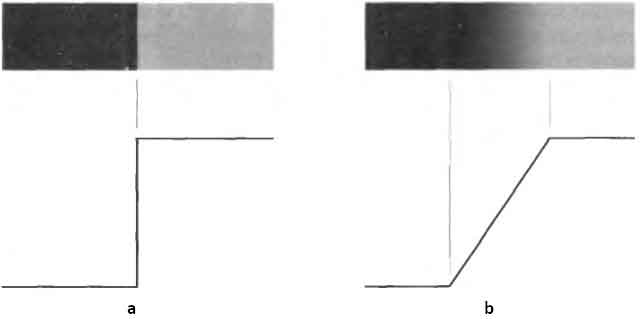
Рисунок 1.3 – (a) Модель ідеального перепаду
яскравості. (b) Модель похилого перепаду яскравості
Область перепаду залежить від якості системи реєстрації, кроку
дискретизації, освітлення. На рисунку 1.4 приведений горизонтальний
профіль перепаду яскравості, його перша і друга похідні. Перша похідна
має постійне ненульове значення на ділянці перепаду, і нульове значення
при постійному рівні яскравості. Друга похідна позитивна в точці
переходу від темної до похилої ділянки, негативна в точці переходу від
похилої до світлої ділянки, і дорівнює нулю на лінійному схилі і
ділянках постійної яскравості.
Можна прийти до висновку, що за першої похідної можна виявити перепад
яскравості в кожної точки зображення. За знаком другої похідної
визначають, чи лежить піксель в темній або світлій частині перепаду.
Властивості другої похідної поблизу перепаду яскравості: 1) два
ненульових (позитивне і негативне) значення для кожного перепаду, що є
небажаним властивістю; 2) уявна пряма лінія, що з'єднує максимальні
позитивні і негативні значення другої похідної, перетинає нульовий
рівень приблизно в середині перепаду яскравості.
Властивість перетину нульового рівня другої похідної корисно для
локалізації середини широких перепадів.
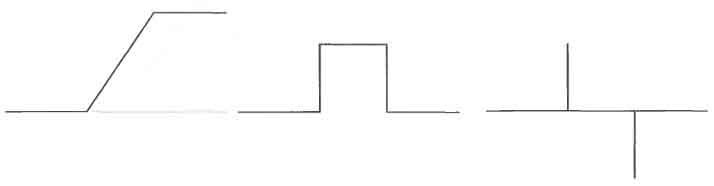
Рисунок 1.4 – Горизонтальний профіль яскравості,
перша і друга похідні
У реальних зображеннях в областях з перепадами яскравості також буде
присутній шум.
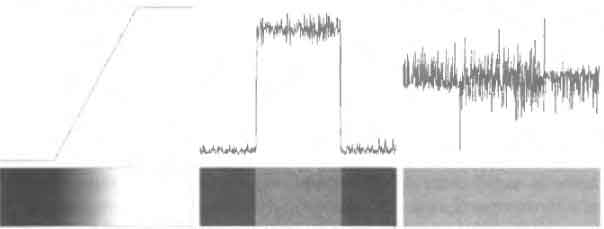
Рисунок 1.5 – Присутність шуму в профілі
яскравості і його вплив на першу і другу похідні
При великій кількості шумів буде важко розпізнати перепад яскравості у
першій похідній. Друга похідна ще більш чутлива до перепадів яскравості.
Тому в практичних завданнях доцільно згладжувати зображення перед
обчисленням похідних.
Оператори градієнта
Градієнт зображення f (x, y) в точці (x, y) – це вектор:
 (1.3)
(1.3)
Модуль вектора:
 (1.4)
(1.4)
Величина дорівнює максимальній швидкості зміни функції.
Напрямок вектора градієнта:
 (1.5)
(1.5)
Обчислення градієнта зображення полягає в отриманні величин приватних
похідних df/dx і df/dy для кожної точки. Перші приватні похідні можна
знайти за допомогою:
а) перехресного градієнта оператора Робертса: Gx = (z9-z5);
Gy = (z8 – z6);
б) оператора Превітта: Gx = (z7+z8+z9) – (z1 + z2 + z3);
Gy = (z3+z6+z9) – (z1 + z4 + z7);
в)оператора Собела: Gx = (z7+2*z8+z9) – (z1 + 2*z2 + z3);
Gy = (z3+2*z6+z9) – (z1 + 2*z4 + z7).
| z1 |
z2 |
z3 |
| z4 |
z5 |
z6 |
| z7 |
z8 |
z9 |
|
|
|
| Околиця |
Маски оператора Робертса |
|
|
|
|
|
| Маски оператора Превітта |
Маски оператора Собела |
Рисунок 1.6 – Околиця 3х3 усередині зображення і
різні маски, застосовані для обчислення градієнта в центральній точці
околиці
Оператор Робертса є незручним, тому що немає чітко вираженого
центрального пікселя. Маски оператора Собела краще масок Превітта тим,
що зменшується ефект згладжування за рахунок надання середнім точкам
більше ваги. Також маски Превітта і Собела можна змінити таким чином,
щоб вони давали максимальний відгук для контурів, спрямованих
діагонально.
Для спрощення обчислення модуля градієнта використовують формулу:
 (1.6)
(1.6)
Лапласіан
Лапласіан двовимірної функції f (x, y) є похідною другого
порядку, що визначається виразом:
 (1.7)
(1.7)
Стосовно до околиць 3х3 використовують вираз:
 (1.8)
(1.8)
Дискретне приближення з використанням діагональних сусідніх елементів має
вигляд:
 (1.9)
(1.9)
|
|
| -1 |
-1 |
-1 |
| -1 |
8 |
-1 |
| -1 |
-1 |
-1 |
|
Рисунок 1.7 – Маски лапласіана, для реалізації
формул (1.8) і (1.9)
Зв'язування контурів і знаходження меж з допомогою локального
опрацювання
Аналізується невелика околиця (3х3 або 5х5) кожної точки (x, y)
зображення, яка зазначена як контурна. Всі крапки, схожі за певними
критеріями, зв'язуються і утворюють контур. Використовують величину
відгуку і напрямок вектора градієнта.
 (1.10)
(1.10)
де Е – заданий невід'ємних поріг (за модулем градієнта).
 (1.11)
(1.11)
де А – заданий невід'ємних кутовий поріг. Напрямок контуру в точці (x,
y) перпендикулярно напрямку вектора градієнта в цій точці.
Піксель в околиці об'єднується з центральним, якщо критерії сходяться.
Процес повторюється для кожної точки з одночасним запам'ятовуванням
знайдених пікселів.
Також для зв'язування контурів використовують глобальний аналіз за
допомогою перетворень Хафа і методів теорії графів.
Порогове опрацювання
Приміром, зображення містить світлі об'єкти на темному тлі, так що
яскравості пікселів об'єкта і фону зосереджені поблизу двох переважаючих
значень. Очевидний спосіб – задати значення порогу T. Тоді будь-яка
точка (x, y), в якій f (x, y)> T, називається точкою об'єкту, а в іншому
випадку – точкою фону.
Більш узагальнений варіант містить об'єкти двох видів і фон. У
багаторівневого порогового перетворення використовуються декілька
порогів яскравості, кожен піксель перевіряється на приналежність
діапазону.
Межа перетворення може розглядатися як операція, при якій проводиться
порівняння з функцією T:
T=T(x,y,p(x,y),f)
(1.12)
де f – зображення, а p(x, y) позначає деяку локальну характеристику
точки (x, y) зображення, наприклад, середню яскравість в околиці з
центром в цій точці. Зображення g(x, y), що отримується в результаті
порогового перетворення, визначається таким чином:
 (1.13)
(1.13)
1 – об'єкт, 2 – фон. Якщо T залежить тільки від f, то поріг глобальний.
Якщо T залежить і від координат x і y, то поріг локальний або
динамічний. Якщо T залежить від p(x, y), то поріг адаптивний.
Опрацювання з глобальним порогом
Це сегментація за допомогою глобального порога T. Успішність методу
залежить від того, наскільки добре розподіляється гістограма.
Поріг – середнє між мінімальним і максимальним значенням яскравості.
Застосовується в задачах технічного контролю, де зазвичай можна керувати
умовами освітлення.
Алгоритм вибору порога T:
1. Обирається якась початкова оцінка порогу T.
2. Проводиться сегментація зображення за допомогою порога T. У
результаті утворюються дві групи пікселів: G1, що складається з пікселів
з яскравістю більше T, і G2, що складається з пікселів з яскравістю меншої або рівної
T.
3. Обчислюються значення μ1 і μ2 середніх яскравостей пікселів по областях
G1 і G2 відповідно.
4. Обчислюється нове значення порога: T = (μ1 + μ2) / 2.
5. Повторюються кроки з 2 по 4 до тих пір, поки різниця значень T при
сусідніх ітераціях не виявиться меншою за значення наперед заданого параметра
T0.
Якщо є підстави вважати, що об'єкт і фон займають однакові площі в
зображенні, гарним початковим порогом T буде середній рівень яскравості
зображення.
Якщо займана об'єктом площа мала в порівнянні з площею фону (або
навпаки), то відповідним початковим порогом буде півсума мінімального і
максимального значень яскравості.
Вирощування областей
Вирощування областей – це процедура, яка групує пікселі або підобласті в
більш великі області за заздалегідь заданими критеріями. Спочатку
береться безліч точок, які є «центрами кристалізації», а потім на них
нарощуються області шляхом приєднання до кожного центру тих пікселів з
числа сусідів, які за своїми властивостями близькі до центру
кристалізації.
Початкові точки обираються на підставі суті завдання. При відсутності
апріорної інформації процедура полягає в обчисленні одного і того ж
набору властивостей для кожного пікселя.
Вибір критеріїв подібності залежить не тільки від обраної задачі, але і
від виду даних (кольорове - монохромне).
Існує проблема зупинки процесу вирощування областей. За ідеєю, необхідно
зупинити процес, коли відсутні пікселі, що задовольняють критеріям.
Потужність алгоритму можна підвищити за рахунок залучення додаткових
критеріїв, наприклад, розміри і форма вирощуваної області. Для цього
необхідна хоча б груба модель очікуваних результатів.
Сегментація за морфологічними вододілами
До цих пір обговорювалися способи сегментації, засновані на трьох
головних підходах: (а) виявлення розривів, (б) порогового опрацювання, (в)
опрацювання областей. Сегментація за вододілами містить в собі багато
концепцій трьох розглянутих підходів. Поняття вододілу засноване на
представленні зображення як тривимірної поверхні, з двома просторовими
координатами і рівнем яскравості. У такій інтерпретації розглядаються
точки 3-х видів: (а) точки локального мінімуму; (б) точки, що
знаходяться на схилі, тобто з яких вода стікає в один локальний мінімум;
(в) точки, що знаходяться на піку, з яких вода стікає більш ніж в один
локальний мінімум. Для кожного лок. мінімуму точки умови (б) називаються
басейном або водозбором. Точки умови (в) – лінії вододілу. Головна мета
– знаходження ліній вододілу. Основна ідея. У локальних мінімумах
проколоті отвори і знизу підступає вода. Коли вода в двох сусідніх
басейнах буде близька до того, щоб злитися, ставиться перегородка. У
міру наповнення водою залишаться видно тільки перегородки. На практиці
метод сегментації по вододілах часто застосовується не до самого
зображенню, а до його градієнту. Локальний мінімум – мале значення
градієнта.
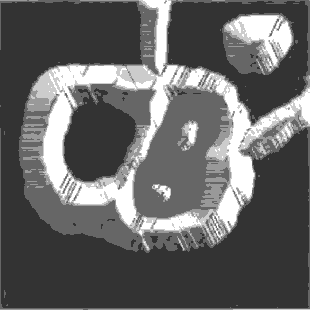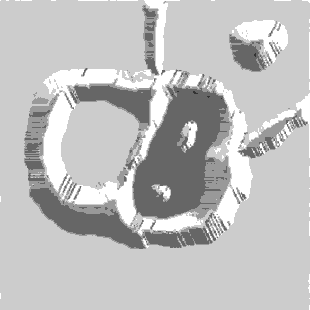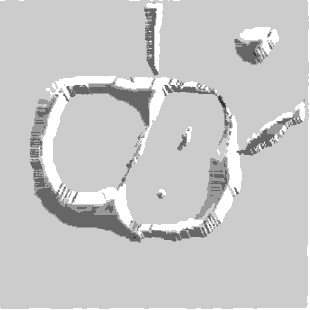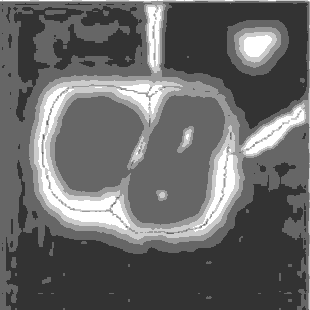
Рисунок 1.8 – Сегментація зображення за
морфологічними вододілами
(Анімація складається з 7 кадрів, 40Кб із
затримкою в 0.3 с між кадрами; затримка до повторного відтворення
складає 1с; кількість циклів відтворення – 10)
Побудова перегородок
Побудова перегородок заснована на двійкових зображеннях, які є
підмножинами двовимірного цілочислового простору. Найпростіший спосіб
побудови ліній поділу для множин, утворених двійковими точками, полягає
у використанні морфологічної дилатації.
Позначимо через М1 і М2 безлічі точок, що відповідають локальним мінімумам
двох розглянутих басейнів. Через Cn-1 (M1) і Cn-1 (M2) позначимо безлічі
точок, покритих водою в цих басейнах на (n-1) кроці заповнення.
Є два басейни – дві компоненти зв'язності (нехай C [n-1] об'єднання
точок цих множин). У міру заповнення басейну утворюється одна компонента
зв'язності. Дві компоненти зв'язності перетворилися в одну, вказує на
те, що відбулося злиття. q – єдина зв'язкова компонента. Необхідно
відзначити, що можна виділити з q дві компоненти зв'язності кроку n-1: q  C[n-1]. C[n-1].
До компонент зв'язності застосовується операція дилатації з умовами:
(1) застосування дилатації повинно обмежуватися безліччю q, (2)
дилатація не повинна виконуватися в тих точках, де це призведе до злиття
множин, так що вони стануть єдиною зв'язковий компонентою.
Зазвичай висота всіх перегородок приймається рівною максимально
можливого рівня яскравості, плюс одиниця. Важливо відзначити, що
перегородки, побудовані із застосуванням даної процедури і є
межами сегментації. Вони є зв'язковими компонентами. Тобто
метод виключає появу розривів у лініях сегментації.
Алгоритм сегментації за вододілами
Нехай М1, М2, ..., MR – безлічі точок, які відповідають локальним
мінімумам поверхні g(x, y) (градієнт зображення). C(Mi) – безліч точок
Mi локального мінімуму. min та max – найменші та найбільші значення
зображення g(s, t). T[n] означає множину точок (s, t), для яких g(s,
t)<n, тобто
T[n] = {(s, t) | g(s, t) < n}.
(1.14)
T [n] – безліч точок, в яких поверхня g(x, y) лежить нижче g(x, y) = n.
При заповненні водою рівень піднімається у вигляді цілочисельних
дискретних збільшень від n = min + 1 до n = max +1. Необхідно на кожному
кроці знати кількість точок, що лежать нижче рівня води. Уявімо, що всі
крапки T [n] (нижче рівня n) відзначені чорним, а решта білим.
Нехай Cn(Mi) позначає безліч точок басейну з локальним мінімумом Mi, які
залиті водою на кроці n. Cn(Mi) можна розглядати як бінарне зображення,
що задається
Cn(Mi) = C(Mi)  T[n].
(1.15) T[n].
(1.15)
Іншими словами Cn (Mi) = 1 у тих точках (x, y), для яких одночасно
виконується (x, y)  C(Mi) і (x, y) C(Mi) і (x, y)  T[n], в інших точках зображення Cn
(Mi) = 0. T[n], в інших точках зображення Cn
(Mi) = 0.
Нехай C [n] – об'єднання залитих водою частин всіх басейнів на кроці n:
C[n] =  Cn(Mi).
(1.16) Cn(Mi).
(1.16)
Тоді C[max + 1] є об'єднання всіх наявних басейнів:
C[max + 1] =  C(Mi).
(1.17) C(Mi).
(1.17)
В алгоритмі не відбувається видалення елементів з множин Cn(Mi) і T[n].
Отже, C [n-1] є підмножиною C[n]. Також C[n] є підмножиною T[n], а
значить і C[n-1] підмножина T[n]. Як результат: кожна компонента
зв'язності безлічі C [n-1] міститься рівно в одній зв'язковий компоненті
безлічі T[n].
Алгоритм знаходження ліній вододілу починається з ініціалізації C[min +
1] = T[min + 1]. Після цього алгоритм виконується рекурентно з припущенням,
що на n-му кроці безліч C[n-1] вже побудована. Для отримання
C[n] з C[n-1] застосовується процедура. Нехай Q[n] – безліч компонент
зв'язності T [n]. Тоді для кожної зв'язковий компоненти q  Q[n] є три можливості:
Q[n] є три можливості:
а) q  C[n-1] – порожня безліч; C[n-1] – порожня безліч;
б) q  C[n-1] містить єдину
компоненту зв'язності безлічі C[n-1]; C[n-1] містить єдину
компоненту зв'язності безлічі C[n-1];
в) q  C[n-1] містить більше
однієї компоненти зв'язності безлічі C[n-1]. C[n-1] містить більше
однієї компоненти зв'язності безлічі C[n-1].
Спосіб побудови C[n] по C[n-1] залежить від того, яка з цих трьох умов
має місце. Умова (а) означає, що зустрівся новий локальний мінімум
(починається наповнення нового басейну); в цьому випадку для побудови
безлічі C[n] компонента q додається до C[n-1]. Умова (б) має місце,
коли q лежить усередині басейну деякого локального мінімуму; в цьому
випадку для побудови безлічі C[n] компонента q також додається до C[n-1].
Умова (в) виникає, коли зустрілися точки гребеня, що розділяють
два або більше басейни. Необхідно побудувати перегородку (або
перегородки). Перегородка товщиною в один піксель будується,
застосовуючи до безлічі q  C[n-1] операцію дилатації по примітиву 3x3,
заповнену одиницями, і потім обмежуючи результат дилатації точками
безлічі q. C[n-1] операцію дилатації по примітиву 3x3,
заповнену одиницями, і потім обмежуючи результат дилатації точками
безлічі q.
Ефективність алгоритму можна підвищити, використовуючи тільки ті
значення n, які відповідають рівням яскравості, що зустрічається в g(x,
y). Значення визначаються за гістограмою.
Використання маркерів
Алгоритм сегментації за вододілами зазвичай призводить до надмірної
сегментації, викликаної шумом і іншими локальними нерівностями на
градієнтному зображенні. Необхідно виконати попередню процедуру опрацювання,
засновану на ідеї маркерів.
Маркер являє собою зв'язкову компоненту, що належить зображенню.
Внутрішні маркери відносяться до об'єктів, що є цікавими, зовнішні маркери
відповідають тлу. Процедура вибору мітки: (1) попереднє опрацювання, і (2)
вироблення критеріїв, яким мають задовольняти маркери. Для зниження
впливу дрібних деталей використовується фільтрація за допомогою згладжуючого фільтра.
Нехай внутрішній маркер визначається як область, (1) оточена точками з
більшою «висотою»; (2) така, що її точки утворюють компоненту
зв'язності, та (3) всі точки якої мають однакові значення яскравості.
Внутрішні маркери, знайдені на згладженому зображенні відповідно до
такого визначення, показані у вигляді світло-сірих плям:
Далі до згладженого зображення застосовується метод сегментації по
вододілах, з тим обмеженням, що в якості локальних мінімумів
розглядаються тільки внутрішні маркери. Отримані в результаті лінії
вододілів, є зовнішніми маркерами. Зовнішні маркери ефективно
розмежовують зображення на області, кожна з яких містить єдиний
внутрішній маркер і частину фону. Після цього задача зводиться до
розділення кожної такої області на об'єкт і фон. Таку спрощену завдання
можна вирішувати багатьма методами. Можна застосувати той же алгоритм
сегментації по вододілах стосовно до кожної області.
Маркер може ґрунтуватися як на зв'язності і значеннях яскравості, так і
на розмірі, формі, текстурі. У сегментації дуже важливими є апріорні
знання.
Використання руху при сегментації. Просторові методи
Один з найпростіших підходів до виявлення змін, що сталися між двома
кадрами f (x, y, ti) і f (x, y, tj), полягає в поелементному порівнянні
цих двох елементів. Один зі способів порівняння – побудова різницевого
зображення, де нерухомі складові взаємно знищуються.
Різницеве зображення можна визначити:
 (1.18)
(1.18)
де Т – заданий поріг. dij (x, y) приймає значення 1 в точці з
просторовими координатами (x, y) тільки в тому випадку, якщо значення
яскравості істотно відрізняються.
При опрацюванні динамічних зображень, усі одиничні пікселі вважаються
результатом руху об'єкта. Такий підхід можливо застосувати, якщо зображення просторово
суміщені, і якщо флуктуації яскравості не виходять за межі значення Т.
На практиці ненульові елементи часто є наслідком шуму. Оскільки вони
утворюють невеликі ізольовані групи точок, то вони видаляються шляхом
знаходження 4 - або 8-ми пов'язаних областей одиничних пікселів. Хоча це
може призвести до пропуску малих і / або повільно рухомих об'єктів.
Для зменшення ймовірності пропуску руху малих об'єктів через шуми
необхідно розглядати послідовність кадрів, щоб ігнорувати зміни, що рідко
зустрічаються.
Послідовність кадрів f (x, y, ti), f (x, y, t2), ..., f (x, y, tn) і f
(x, y, ti) – опорний кадр. Накопичене різницеве зображення (НРЗ)
формується шляхом порівняння опорного зображення з кожним наступним
кадром. Для кожного пікселя ведеться лічильник, який накопичує значення,
якщо є відмінність між опорним і поточним кадром.
Розглядають абсолютні, позитивні і негативні НРЗ. Опорне зображення R
(x, y) і нехай k позначає момент часу tk, тобто f (x, y, k) = f (x, y,
tk). Вважаємо також R (x, y) = f (x, y, 1). Тоді для будь-якого k> 1
визначається:
 (1.19)
(1.19)
 (1.20)
(1.20)
 (1.21)
(1.21)
Початкові значення лічильників нульові, розміри НРЗ збігаються з
розмірами початкового зображення.

Рисунок 1.9 – Накопичені різницеві зображення
прямокутного об'єкту:
абсолютне, позитивне і негативне НРЗ
На практиці не завжди є можливість отримати опорне зображення, що складається
лише з нерухомих об'єктів. Його доводиться будувати на підставі набору
зображень, що містить один або більше рухомих об'єктів.
Висновок
З наведеного вище матеріалу видно, що існує велика кількість методів
сегментації зображень. Хоча набір методів не вичерпний, вони є
характерними представниками техніки сегментації. Також можна прийти до
висновку, що різні техніки можна поєднувати. Приміром, є можливість
поєднати просторову сегментацію з сегментацією рухомих об'єктів.
Список літератури
-
Гонсалес Р. Цифровая обработка изображений / Гонсалес Р., Вудс Р.; пер. с англ. П. А. Чочиа
- Москва: Техносфера, 2005, С. 812-916.
-
Segmentation (image processing) [Електронний ресурс] –
Режим доступу до статті:
http://en.wikipedia.org/wiki/Segmentation_(image_processing)
-
Универсальная классификация алгоритмов сегментации изображений [Електронний ресурс]
/ С.В. Поршнев, А.О. Левашкина – Режим доступу до статті:
http://www.jurnal.org/articles/2008/inf23.html
-
D.J.Williams and M.Shas. “Edge Contours Using Multiple Scales”.
Computer Vision, Graphics and Image Processing, 51, 1990,
pp.256-274.
-
V. Lacroix. “The Primary Raster: A Multiresolution Image
Description”. In Proceedings of the 10th International Conference on
Pattern Recognition, 1990, pp. 903-907.
-
J.F.Canny. “A Computational Approach to Edge Detection”. IEEE
Transactions on Pattern Analysis and Machine Intelligence, 8(6), Nov
1986, pp. 679-698.
-
D. Ziou and S. Tabbone. “A Multi-Scale Edge Detector”. Pattern
Recognition, 26(9), 1993, pp.1305-1314.
-
T. Lindeberg. “Edge Detection and Ridge Detection with Automatic
Scale Selection”. In Proceedings of IEEE, International Conference
on Computer Vision and Pattern Recognition, San Francisco, 1996, pp.
465-470.
-
William K. Pratt Digital Image Processing,
Wiley-Interscience Publication, 2001, pp. 551-589.
-
L. M. J. Florack, B. M. ter Haar Romeny, J. J. Koenderink, and M. A.
Viergever. “Scale and the diferential structure of images”. Image
and Vision Computing, 10(6), Jul 1992, pp.376-388.
|

