When starting its productive-economic activity, each enterprise must possess a certain sum of money. These money recourses are used by the enterprise to buy at the market or from the other enterprises according to the contracts raw materials, stuff and fuels, pay the bills for electricity, pay wages to its employees, carry expenses for developing new products; these all make together one of the main parameters of management which got the title of the "reversible capital of the enterprise".

        In the conditions of the market relationship the reversible capital acquires extreme importance. It is it that presents itself as a part of the productive capital, which completely transfers its value onto the newly made product and comes back to the proprietor in the form of money at the end of each circulation of the capital. Thus, the reversible capital appears to be an important criterion in defining the profits of the enterprise [1].

        As far as the methods and models of the management of the reversible capital in the exactly determined surrounding are studied well enough ([2], [3]), there have been created methodical aids for them. We are going to consider the management in the stochastic surrounding, when the result of the work of a business-unit is not known beforehand, but depends on numerous casual factors.

The actuality of the theme under Investigation

        One of the most important problems typical for the majority of the enterprises nowadays is a sharp lack of the reversible capital; in many cases this lack can be compensated by the borrowed reversible capital. To secure the appropriate state of the reversible capital in practice is a complicated task. The reversible capital is affected by many factors, the latter being mostly negative. As a result, there appears the deficiency of the means in circulation, and the financial status of the enterprise becomes unstable. Consequently, for the efficient work of the enterprises the task of the optimal management of their own reversible capital is of paramount importance.

        The actuality of this article gives no rise to doubt, as far as setting the task of the optimal management of a business-unit’s finance will allow to create an efficient investment portfolio to maximize the expected income.

The purposes and the tasks of the research

        The purpose of this work is to represent the model of the financial stream of a business-unit which functions in a stochastic surrounding. Under investigation is the task of optimal management of their own reversible capital by a business-unit, which is formulated as the task of minimizing the risk of a business-unit’s functioning at the set level of its expected efficiency. It is presented that the above mentioned task may be brought to a standard task of choosing the most efficient portfolio. When doing it, Sharp’s method allows to model the most qualitative investment into the stochastic surrounding which permits to consider and regulate the degree of the financial investment’s risk. The measure of the effectiveness, deduced by Sharp (the ratio of the expected income to the risk), allows to pass from the multi-criteria task to the task of optimizing one criterion, which finds a wider application in practice.

A review of the research and elaborations on the theme

        The problem of managing the reversible capital has been dealt with by many scientists of both national and foreign schools. In the works of the native economists V.Y. Adamov, M.I. Bakanov, Y.F. Borisov, I.N. Vasilyeva, O.I. Volkova, V.G. Gribov, V.P. Gruzinov, B.V. Gubin, N.L. Zaytsev, S.D. Ilyenkova, A.A. Kazakov, A.A. Lebedev, N.V. Minayev, I.K. Ozerov, A.A. Petrov, I.V. Romanenko, V.M. Semyonov, I.V. Sergeyev, V.I. Strazhev, V.V. Hohlov theoretical and practical statements in the field of the conceptual apparatus, the essence and structure of the agent’s reversible capital, of the economy and the efficiency of its usage are reflected. The works by K. Alfred, A.V. Grachev, A.I. Kovshar, L.A. Kostyrko, V.P. Kryzhakovsky, V.I. Lapenkov, V.I. Lyuter, L.A. Rotshtein are dedicated to the problems of managing the reversible capital and forecasting as one of the subsets of the analysis system.

        Practical aspects in the field of the reversible capital management policy have not been studied sufficiently, which causes considerable difficulties in the practical activity. In the candidate’s opinion, it is important not only to elicit the peculiarities of the economic agent’s management of the reversible capital, but also to improve them, taking into account the level of the industrial organization development, on the ground of which to define the mechanism of the management for taking the conscious managing decisions.

        The actuality of the problem and the unsolved tasks, connected with the mechanism of the reversible capital’ management, call for the necessity of carrying on the work for the improvement of the analysis’ methods and the mechanism of the reversible means management.

The supposed scientific novelty

        The scientific novelty of the dissertation lies in the complex approach to modeling and analysis of the optimal placement of the assets in the stochastic investment surrounding. A concrete accretion of scientific knowledge is characterized by the following propositions:

• the model is proposed and the dynamic task of choosing the portfolio is solved by the additional criterion by Sharp;
• the improved mechanism of the reversible means management is produced

The general statement of the task

        The task is formulated as the task of choosing the optimal parts of the withdrawn means which minimize the dispersion of the financial result of the business process at the fixed level of the expected profit (the dual task is the task of maximizing the expected profit at the fixed level of risk). The essential stochastic business process (EBP) — is one operation with the duration , at the beginning of which the sum , is invested (spent), and in t time a bigger sum comes back , the latter not known beforehand, but is a casual quantity. If d — is the factor of discounting, — the start level of the reversible capital, — are (stochastic) factors of profitability, then in a general case the problem looks like:

       

        where ER — is the fixed minimum of the expected income, [...] means a mathematical expectation at the zero moment of time, optimization being conducted with taking into account the limits (balances) for the movement of the financial means:

       

        The first equation reflects the change of the reversible capital as a result of realization of a business process during one period, the second one demonstrates the quantity of the means being withdrawn for the usage through the share in the general sum of the reversible capital, the third one reflects the division of the whole sum of the reversible capital for consumption and reinvestment.

        Here and further it is supposed that casual quantities can’t be smaller than -1, thus, the quantity of the reversible capital, got as a result of business process realization is always positive.

        Using formulas (4) — (6), the expression for NPV (without taking into account the starting investments , which are an additive constant and do not influence the optimization) can be transformed into the following:

       

        This way the task of the optimal management of the financial stream of a business-unite makes the task of the optimal choice of reinvestment shares , in such a way that the dispersion of the result of the business-unite work is minimum at the fixed mathematic expectation of the result.

        The task formulated above at the consequent transformation of the variable quantities of management appears to be the task of constructing the optimal investment portfolio.

        Let us introduce the following designations. Let Ri — be a discounting profit for the investment in a business-unit (a casual quantity during I periods (discounting factor of business growth) e.g.

       

        Let also “weights”, corresponding to different Ri, be designated through

       

        Then NPV of the financial stream of a business-unite looks like (see formula (7), without counting the starting investments):

       

        It is possible to show that on this condition between the sets of the variable management there exists the reverse correspondence

       

        for the meanings , satisfying

       

        With this solution of the initial problem

       

        Let us note that problem (13) — is the problem of the optimal portfolio choice, if under Ri (discounting stochastic factor of business raise) we understand "profitability of the assets", and under are the weights of these assets in the portfolio. Here the limitation (15) corresponds to a particular case of the problem of the optimal portfolio choice with the ban for the "short positions".

        The most important role in the management is played by the theory of the optimal portfolio which is connected with the problem of choosing the most efficient portfolio, capable to maximize the expected profitability at some level of risk, suitable for the investor. Theoretically possible methods allow to give the definition of the "expected profitability" and "risk" of the portfolio, when the statistic data — allow to get an estimate of these characteristics.

        are the weights of these assets in the portfolio. Here the limitation (15) corresponds to a particular case of the problem of the optimal portfolio choice with the ban for the "short positions". The most important role in the management is played by the theory of the optimal portfolio which is connected with the problem of choosing the most efficient portfolio, capable to maximize the expected profitability at some level of risk, suitable for the investor. Theoretically possible methods allow to give the definition of the "expected profitability" and "risk" of the portfolio, when the statistic data — allow to get an estimate of these characteristics.If the investor is to choose one of the efficient portfolios, the optimal one will be the most preferable of them.

        Harry Markovits has created the mathematic model, which demonstrates how investors can at most low down the risk at the fixed rate of profitability. Markovits’ approach begins with the supposition, that at the moment the investor has a concrete sum of money for his investment. This money will be invested for a certain period of time, which is called the period of proprietorship. At the end of the period of proprietorship the investor sells the product got as a result of his investment at the beginning of the period; after that he either spends the received income for consumption, or reinvests it into the development of the enterprise (or does both simultaneously [4].

Figure 1 - Border of efficiency of Makrovitsa (gif-animation, 6 shots, 5 cycles, size 33,9 Кб, software MP GIF Animator)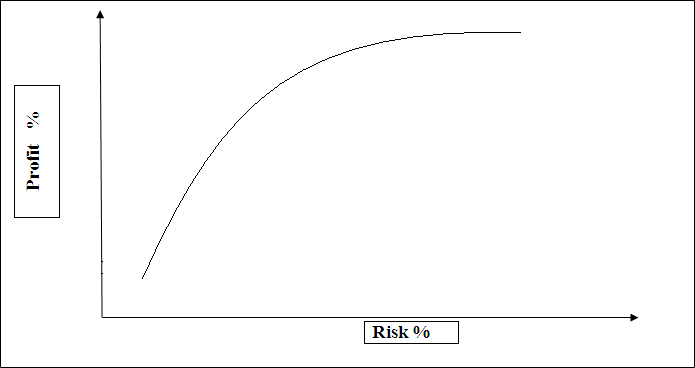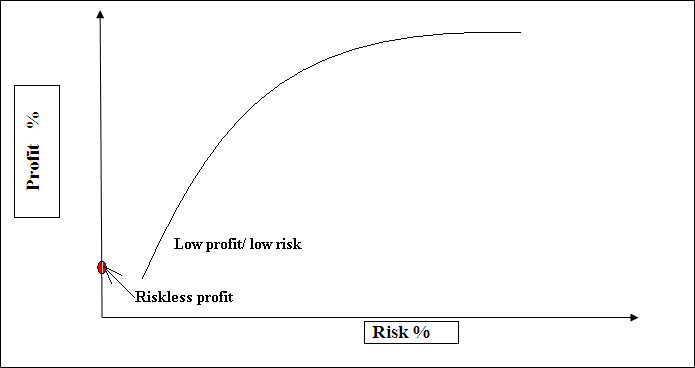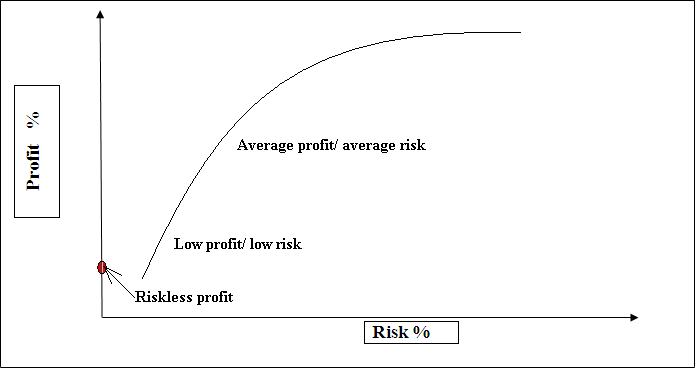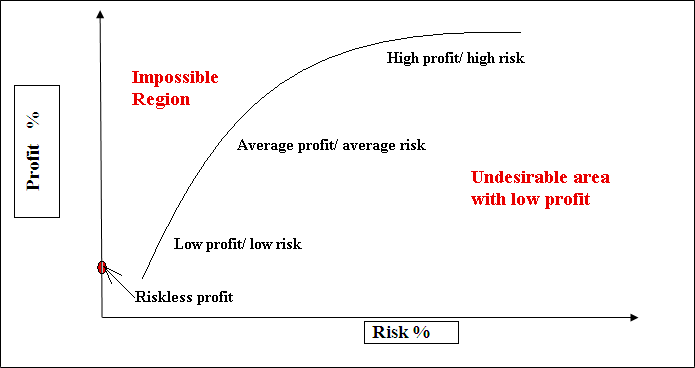

        William Sharp used the results of G.Markovits’ research as a starting point for the further investigation, in the course of which he defined the influence of Markovits’ model on the financial assets’ prices, having supposed that at any moment the prices for the financial assets will be changing to support a balance of supply and demand for every risky asset [5]. The assets’ structure deduced in Sharp’s theoretical statements, is widely used as the basis for regulating risk rate in many branches of financial theory and practice nowadays. In particular, when estimating the efficiency of investments in the stochastic surrounding, such measure of the efficiency as Sharp’s ratio (the ratio of the expected income to risk) became widely spread.

        In our work we will make the model [3] more complicated, adding William Sharp’s supplementary criterion.

       

        Where R— is a profitability of the portfolio (asset); Rf — is a profitability from the alternative investment (as a rule, it is a non-risky interest-bearing rate); E[R — Rf] — is a mathematical expectation.

        The numerator is a middle difference of the fund efficiency and the non-risky rate (equal to the rate of refinancing). The standard deviation in the denominator shows the measure of risk, e.g. the possibility of getting by the investor a different income if compared with the one expected. As far as we risk when giving the money into the management in the fund market instead of putting it to the bank, we expect to get higher profits than the simple bank deposit, and this extra profit will be as if bonus for risk. The higher is the ratio of the bonus to the risk, the better is the fund, e.g. when choosing the fund, the preferable ones will be those which possess a higher Sharp’s factor. It is reasonable to suppose that such a choice will be ideal.

Findings

        In the work under consideration a model of a business unite which functions in a stochastic surrounding (with the undetermined level of profitability) has been offered. The task of the optimal management of the business-unit’s financial stream, as the choice of the shares being withdrawn, which minimizes the dispersion of the results of a business-unit’s work at the offered level of the expected discounted income has been formulated.

        In the work a review of the existing kinds of the investing portfolio has been made as well as the mostly wide-spread approaches at its creating in the conditions of the stochastic surrounding have been analyzed. At the same time, it is Sharp’s approach which allows us to model the investments in the stochastic surrounding qualitatively and to consider and regulate the risk rate of the financial investments. The rate of the efficiency, deduced by Sharp (the ratio of the expected income to risk) allows us to pass from a multi-criteria task to the task of a single criterion optimization, which can find a wide practical application.

Literature

1. Г.Л. Азоев. Конкуренция, анализ, стратегия, практика. — М.: Центр экономики и маркетинга, 1996 — 208с.
2. Крушвиц Л., Шефер Д., Шваке М. Финансирование и инвестиции. Сборник задач и решений, Питер, 2000. — 297 c.
3. Markowitz H.M. Portfolio selection, Journal of Finance, 1952, vol. 7, N1.
4. Соколов Д.Г. Бизнес-единица в стохастическом окружении: задача оптимального реинвестирования /Управление большими системами /Сборник трудов молодых ученых. Выпуск 4. Общая редакция — Д.А. Новиков. М.: ИПУ РАН, 2003. — 127 с.
5. Винник А.А., Ириков В.А., Парфенова А.А. Подготовка и принятие решений по управлению финансовыми потоками бизнес-единиц. — М.: ИПУ РАН, 1999. — 95 с.
6. Винник А.А., Дранко О.И., Ириков В.А. Движение оборотного капитала. Подготовка и принятие решений по управлению пассивами и активами. М.: ИПУ РАН, 1999. — 87 с.
7. Соколов Д.Г. Параметрическое исследование реализации бизнес-процесса. Магистерская диссертация, МФТИ, 2000. — 110 с.
8. Акофф Р. Планирование будущего корпорации. - М.: Прогресс, 1999.
9. Максимов В.И., Никонов О.И, Моделирование риска и рисковых ситуаций. Учебное пособие. Екатеринбург 2004. — 82 с.
10. Баркалов С.А., Бакунец О.Н., Гуреева И.В., Колпачев В.Н,. Руссман И.Б. Оптимизационные модели распределения инвестиций на предприятии по видам деятельности. М.: ИПУРАН, 2002. — 68 с.
11. В.С. Анфилатов, А.А. Емельянова, А.А. Кукушкин. Системный анализ в управлении. Учебное пособие. — М.: Финансы и статистика 2002. — 368 с.
12. Е.П. Голубков. Маркетинговые исследования: теория, методология и практика. — М.: Финпресс, 1998. — 416 с.

* — The work is in development for the current day and is planned to be finished by December 1st, 2010. The paper and relevant materials can be obtained either form author or its supervisor after that date.