Signature Analysis by Shift Registers
[English] [German] [Russian]
[Hints]
During the early years of integrated circuit applications
to digital systems guided probing was used as a
support to ease fault location if a deviation from regular behavior had
been observed /1,2/. The principle was based on so called "signatures", a certain data sequence which can be
observed at a particular device location if a fixed input sequence is
applied to the circuit. Generally test input sequences are used for such
a purpose, but the idea is that also any operational input sequence can
be used as well if it is simply long enough and deviates in case of a
device fault from the fault-free situation. Of course, it is very
tedious to evaluate long sequences bit by bit, hence feedback shift
registers are very useful because they can concentrate the information
contained in long bit strings to their length, in practical cases only a
couple of bytes. Such a reduced length sequence is called signature for
each signal point of the circuit under consideration. With a particular
input pattern a set of signatures can be determined once for all to
describe the correct circuit behavior. If part of the circuit turns out
to be faulty, e.g. carrying a permanent error signal like stuck-at-0 or
stuck-at-1, a probing of all signal nodes will quickly detect the origin
of the deviation, because the corresponding signature will deviate from
the original fault-free value.
A theoretical investigation of this approach is based on polynomials describing error detecting codes /3,4/, in particular cyclic codes based on generator polynomials. For partical applications it is sufficient to state that a primitive feedback polynomial will cause a shift sequence of maximal length in such a register. If we assume 16 bits as the register length, such a polynomial provides for a length of 216 — 1 or 65535 digits. Any deviation from normal behavior will be detectable except if it is a multiple of the generator polynomial, hence there is a very low probability of 2-16 for not detecting a particular error situation.
Since the construction of such a shift register is very simple, a Java applet was designed to provide for a remote simulation mechanism in order to visualize the signature conditions outlined above. A simple layout of register positions and feedback connections is indicated in fig.1. Each feedback connection is added mod 2 to the input bit E producing an input signal V to the left-most register position which is then shifted right with the whole register. The right-most position is lost.
As can be concluded from fig.1 the feedback polynomial involves certain positions, namely
f(x) = x16 + x9 + x7 + x4 + 1.
Hence there will be a remainder after 16 or more steps which is different from zero provided the input is different from the zero sequence, the only input to be excluded in practical operations. To avoid confusions by long bit strings it is recommended to use hexadecimal numbers to describe any register contents. By proprietary reasons 0 through 9, then A, C, F, H, P, and U have been assigned to represent the 16 different 4-bit values rather than the conventional 0 through 9, then A, B, C, D, E, and F.
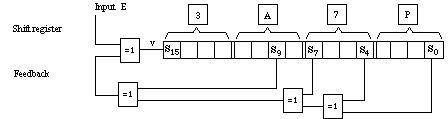
Fig. 1. A 16 bit feedback shift register (E input)
Fig. 2 shows a simple circuit example consisting of 2 flipflops and a
couple of two-input NAND gates and inverters. All the circuit nodes
carry an identification, either upper case letters for the 5 inputs or
lower case letters for internal nodes or the output. T is the clock
input,  a reset input, SEL a mode select signal, D and SDI
are special data inputs, whereas y is the output. Apparently the 4 input
signals except T determine via intermediate variables a, b, c, and d
the next state of the D flipflops.
a reset input, SEL a mode select signal, D and SDI
are special data inputs, whereas y is the output. Apparently the 4 input
signals except T determine via intermediate variables a, b, c, and d
the next state of the D flipflops.
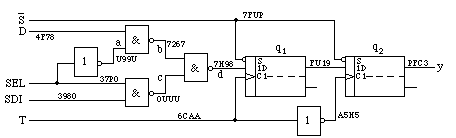
Fig. 2. Example circuit, fault-free situation
Table 1 lists a certain set of corresponding signals to achieve an
output sequence of both flipflops as indicated. Since the flipflops are
positive edge sensitive it is assumed that any line contains stabilized
signal values before the transition of the T signal, whereas the
flipflop values are obtained after clock transition. This means for line
no. 1 that  sets both flipflops to 11 and remains inactive up to
line no. 14. In line no. 2 D, SEL, and SDI produce signal d=0 which
resets flipflop q1=0 after the clock transition to 1. In line
no. 3 only q2 is reset, due to the negative clock edge 10,
all other signals remain unchanged.
sets both flipflops to 11 and remains inactive up to
line no. 14. In line no. 2 D, SEL, and SDI produce signal d=0 which
resets flipflop q1=0 after the clock transition to 1. In line
no. 3 only q2 is reset, due to the negative clock edge 10,
all other signals remain unchanged.
| i | S | D | SEL | SDI | T | a | b | c | d | q1 | q2=y |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 5 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 6 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 8 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 11 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 12 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 14 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 15 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 16 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
Of course it is a tedious job to determine all the signatures which are listed at the circuit nodes of fig. 2 by pencil and paper. But it is quite easy if the simulator applet is used. Simply mark the feedback switches according to the polynominal, select a column in table 1 for input, push restart, and step the register through its 16 feedback steps, then read and compare the result. All the signatures in fig. 2 can thus easily be verified.
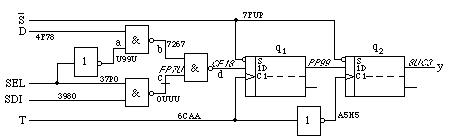
Fig. 3. Example circuit with a broken connection for node c
What happens in case of circuit faults? It may be expected that some
signatures will deviate from those listed in fig. 2. A special case is
shown in fig. 3. where signal line c is assumed to have been interrupted
leaving an open output from the generating NAND gate. This should
produce the same signature OUUU as in fig. 2 because the fault cannot
influence this signal. But the next input now also is open, hence it
would erroneously produce the complement of b by the next NAND gate.
This means that the open input carries a sequence of 1 bits only if TTL
implementation is assumed. Hence the faulty signature is FP7U which
eventually will not be visible if NAND gate d contains internally an
open input. But the changed output signature of d = CF18 (equivalent to 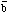 in table 1) definitely locates the fault. It is now quite
easy to verify all the other signatures in fig. 3.
in table 1) definitely locates the fault. It is now quite
easy to verify all the other signatures in fig. 3.
Notice that for the current example a test sequence of 16 bits in length has been used. But since up to a length of 65535 input steps always different register contents will show up, also any arbitrary input sequence will have a high probability to detect eventual errors in the circuit. Feedback shift registers as described here can also produce pseudo-random sequences to be used for probability testing rather than making use of deterministic test sequences.
References
- Frohwerk, R.A. Signature analysis, Hewlett-Packard J. 28, Nr. 9, 1977, p. 2...8
- Bennetts, R.G. Design of testable logic circuits, Addison Wesley, London, 1984
- Leisengang, D. Signaturanalyse in der Datenverarbeitung - Anwendungen und Beispiele, Elektronik 21, 21.10.1983, S. 67...72
- Peterson, W.W. Error-correcting codes, 2. ed., Weldon, E.J. MIT Press, Cambridge, Mass, 1988
[Hints]
[English] [German] [Russian]
Last change: April 1, 2004