Сигнатурный анализ с использованием сдвиговых регистров
[Английский] [Немецкий] [Русский]
[Указания]
Раннее для обнаружения неисправностей, при отклонении работы схемы
от нормального профиля, в интегральных схемах для цифровых систем
использовался метод управляемого зондирования
/1,2/. Его принцип основан на применении т.н. "сигнатур"
- определённых цифровых последовательностей на определённых выходах
устройства, при подаче на вход схемы фиксированного сигнала. Как
правило, для этой цели используется тестовая входная последовательность,
однако может быть использована также и любая другая рабочая входная
последовательность, если она достаточно длинная и отличается в случае
ошибки устройства от значения в безошибочном состоянии. Конечно, это
очень утомительно побитно анализировать длинную последовательность,
поэтому очень удобно применять сдвиговые регистры с обратной связью,
т.к. они могут сконцентрировать информацию, содержащуюся в длинной
битовой последовательности, практически, в нескольких битах. Такая
уменьшенная в длине последовательность называется сигнатурой для каждой
рассматриваемой сигнальной точки схемы. Для каждой входной
последовательности жёстко определяется сигнатура, которая описывает
корректную работу схемы. Если одна из частей схемы выдаёт ошибку,
например, определённый сигнал неисправности типа "константный 0"
(stuck-at-0) или "константная 1" (stuck-at-1), зондирование всех
сигнальных узлов быстро определит источник отклонения, т.к.
соответствующая сигнатура будет отличатся от сигнатуры в безошибочном
состоянии.
Теоретическое исследование этого подхода основано на полиномах, описывающих обнаруживающие ошибку коды /3,4/, в частности циклические коды, основанные на порождающих многочленах. Для практического применения достаточно, чтобы исходный полином обратной связи определял в подобном регистре сдвиговую последовательность максимальной длины. Если мы предполагаем, что длина регистра 16 бит, такой полином предусматривает длину 216 — 1 или 65535 знаков. Любое отклонение от нормальной работы может быть обнаружено, за исключением случая, когда результат кратен порождающему многочлену. Поэтому существует очень низкая вероятность (2-16) того, что такая ошибочная ситуация будет обнаружена.
Так как построение такого сдвигового регистра не представляет трудности, для реализации удалённого механизма моделирования работы регистра был реализован Java-апплет. На рисунке 1 представлена упрощённая схема, содержащая регистры и обратные связи. Каждая обратная связь суммируется по модулю 2 с входом E, определяя входной сигнал V в самой крайней левой позиции регистра, который затем сдвигается вправо со всем содержанием регистра. При этом правое крайнее положение теряется.
Как можно заключить из рисунка 1, полином обратной связи использует определённые позиции. А именно
f(x) = x16 + x9 + x7 + x4 + 1.
Поэтому после 16-того шага и далее появляется остаток, который отличается от нуля и который исключается из дальнейших операций. Для избежания путаницы при вводе длинной строки битов, рекомендуется использовать ввод в шестнадцатиричном форме, для описания содержания регистра. В следствие некоторых причин используются символы 0 - 9 и A, C, F, H, P, U вместо обычных 0 - 9, A, B, C, D, E, F.
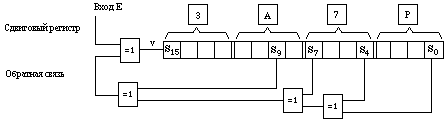
Рисунок 1. 16-тибитный сдвиговый регистр с обратной связью (вход E)
На рисунке 2 представлена простая схема, состоящая из 2 тригеров,
нескольких схем "И-НЕ" и инверторов. T - вход синхронизации, 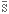 - входной сигнал сброса, SEL - сигнал выбора режима работы,
D и SDI - специальные входные сигналы, а y - выходной сигнал. Очевидно,
что 4 входных сигнала, исключая T, определяют через промежуточные
переменные a, b, c и d последующее состояние D-триггеров.
- входной сигнал сброса, SEL - сигнал выбора режима работы,
D и SDI - специальные входные сигналы, а y - выходной сигнал. Очевидно,
что 4 входных сигнала, исключая T, определяют через промежуточные
переменные a, b, c и d последующее состояние D-триггеров.

Рисунок 2. Пример схемы в безошибочном состоянии
В таблице 1 представлены сигналы для достижения выходной
последовательности обоих триггеров, также представленных в таблице. Так
как триггеры чувствительны к положительному фронту импульса,
предполагается, что любая строка содержит стабильные значения сигнала
перед переходом T сигнала, тогда как значения триггеров получаются после
тактового перехода. Для строки 1 это значит, что 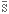 устанавливает оба триггера в 11 и сохраняет их неактивными
до выполнения строки 14. В строке 2 D, SEL и SDI производят сигнал d=0,
который сбрасывает триггер q1=0 в 1 после тактового перехода.
В строке 3 сбрасывается только q2, в следствие
отрицательного фронта синхроимпульса. Все остальные сигналы остаются
неизменяемыми.
устанавливает оба триггера в 11 и сохраняет их неактивными
до выполнения строки 14. В строке 2 D, SEL и SDI производят сигнал d=0,
который сбрасывает триггер q1=0 в 1 после тактового перехода.
В строке 3 сбрасывается только q2, в следствие
отрицательного фронта синхроимпульса. Все остальные сигналы остаются
неизменяемыми.
| i | S | D | SEL | SDI | T | a | b | c | d | q1 | q2=y |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 5 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 6 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 8 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 11 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 12 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 14 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 15 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 16 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
Конечно, это утомительная работа вручную определить все сигнатуры, которые перечислены в узлах схемы на рисунке 2. Но это становится просто сделать, используя разработанный апплет. Нужно только указать обратные связи соответствующие полиному, выбрать строку в таблице 1 в качестве входа, нажать кнопку "Перезапуск" и выполнить 16 шагов, а затем получить и сравнить результат. Все сигнатуры на рисунке 2 могут быть легко проверены.
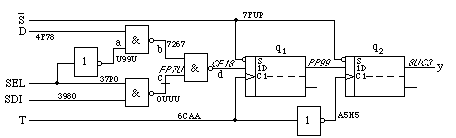
Рисунок 3. Пример схемы с оборванной связью для узла c
Что может случиться в случае ошибки в схеме? Ожидается, что
некоторые сигнатуры могут отклоняться от сигнатур, перечисленных на
рисунке 2. Особый случай показан на рисунке 3, на котором сигнал c
оборван и оставляет выход от формирующей схемы "И-НЕ" открытым. В этом
случае будет сформирована такая же сигнатура 0UUU как и на рисунке 2,
т.к. ошибка не влияет на этот сигнал. Но следующий вход остаётся также
открытым, поэтому будет неправильно сформировано дополнение для b в
следующей схеме "И-НЕ". Это значит, что открытый вход будет формировать
последовательность, состоящую из одних 1, если предполагается, что
используется ТТЛ-схема. Сигнатура ошибки в этом случае будет FP7U,
которая в итоге не будет видна, если схема "И-НЕ" d содержит внутри
открытый вход. Однако изменится выходная сигнатура d равная CF18
(аналогичная 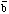 в таблице 1), которая точно локализует
ошибку. Теперь довольно легко проверить другие сигнатуры на рисунке 3.
в таблице 1), которая точно локализует
ошибку. Теперь довольно легко проверить другие сигнатуры на рисунке 3.
В данном примере использовалась тестовая последовательность длинною 16 бит. Увеличение длины входной последовательности до 65535 будет формировать другое содержание регистра. Также любая другая случайная входная последовательность будет иметь большую вероятность обнаружения возможных ошибок в схеме. Сдвиговые регистры с обратной связью могут также формировать псевдо-случайные последовательности для использования при вероятностном тестировании, что лучше чем использование детерминированных тестовых последовательностей.
Литература
- Frohwerk, R.A. Signature analysis, Hewlett-Packard J. 28, Nr. 9, 1977, p. 2...8
- Bennetts, R.G. Design of testable logic circuits, Addison Wesley, London, 1984
- Leisengang, D. Signaturanalyse in der Datenverarbeitung - Anwendungen und Beispiele, Elektronik 21, 21.10.1983, S. 67...72
- Peterson, W.W. Error-correcting codes, 2. ed., Weldon, E.J. MIT Press, Cambridge, Mass, 1988
[Указания]
[Английский] [Немецкий] [Русский]
Последнее изменение: 19 Апреля 2004