Signaturanalyse
[Englisch] [Deutsch] [Russisch]
[Hinweise]
Die vorangehenden Abschnitte machen deutlich, dass eine Testbestimmung
für größere Schaltwerke leicht so aufwendig werden
kann, dass ihre
Durchführung aus Kostengünden nicht mehr zu rechtfertigen
ist. Aus
diesem Grund sind andere Wege notwendig, das Testproblem von
Schaltwerken zu lösen. Die Signaturanalyse bietet dazu einen
Ansatz,
der vor allem auch zur Fehlerlokalisierung vorgeschlagen wurde.
Bei der Signaturanalyse bleibt der Entwurf unbeeinflusst von Rücksichten auf die Prüfmöglichkeiten. Das Prinzip zielt darauf ab, eindeutige Daten für jeden Signalknoten des Schaltwerks bereitzustellen, so dass alle fehlerfreien Werte dieser Information als Vergleich für den Test zur Verfügung stehen. Offenbar sind zahlreiche Alternativen hierfür denkbar. Die Signatur des Knotens ist eine solche Alternative mit weitgehend reduzierter Informationsmenge.
Nach einem Vorschlag der Firma Hewlett-Packard, die als erste Prüfgeräte auf dieser Basis vorgeschlagen hat /1/, lässt sich die Signatur am einfachsten mit linearen rückgekoppelten Schieberegistern erzeugen, wenn dabei ein primitives Rückkopplungspolynom verwendet wird. Wie die Kodierungstheorie nachweist, erlauben solche Rückkopplungen bei gegebener Stellenzahl entweder ein autonomes Durchlaufen einer maximalen Zustandsfolge oder die Division einer Eingangsfolge durch ein durch die Rückkopplungen bestimmtes Generatorpolynom. Um ein vertieftes Eingehen auf die Kodierungtheorie an dieser Stelle zu vermeiden, soll die Signaturanalyse mit einigen Beispielen näher erläutert werden.
Beispiel 1: Schieberegister zur
Signaturanalyse
Gegeben ist die folgende Anordnung /2/:
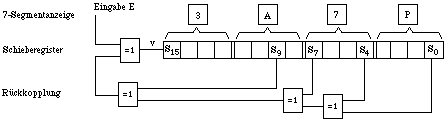
Wie man erkennt, wird der Eingang mod 2 zu gewissen Stellenwerten des Polynoms addiert und auf diese Weise der Wert der höchsten Stelle zum nachfolgenden Zeitpunkt ermittelt. Über eine nicht gezeichnete Taktschaltung werden gleichzeitig alle Stellen nach rechts verschoben. Eine 7-Segment-Anzeige sorgt dafür, dass der jeweilige Registerinhalt als vierstellige Hexadezimalzahl ausgelesen werden kann, wobei firmenorientiert die Ziffernzuordnungen 0, 1, ..., 9, dann aber A, C, F, H, P, U statt A, B, C, D, E, F zur angeblich besseren Anzeige verwendet werden.
Man kann sich leicht überlegen, dass das Register beim Fortschalten und einem Eingabewert 0 entweder den Nullzustand anzeigt und diesen beibehält oder aber die gesamte Menge von 216 - 1 Zuständen durchläuft, sofern der Inhalt anfangs von Null verschieden ist. Letzteres wird durch das Rückkopplungspolynom gewährleistet, das durch Nullsetzen des Generatorpolynoms entsteht, solange die Eingabe Null blebt:
x16 = x9 + x7 + x4 + 1.
Dies ist aus der Schaltung ablesbar und entspricht dem irreduziblen, primitiven Polynom
f(x) = x16 + x9 + 7 + x4 + 1.
Der Prüfbetrieb benutzt als Eingabe die Bitfolge, die an einem beliebigen Signalknoten des Schaltwerks mit Hilfe einer Prüfspitze abgegriffen werde kann. Für eine bestimmte Zahl von Taktschritten wird das Register mit diesen Daten fortgeschaltet, so dass anschließend der Registerinhalt als Signatur der Knoteninformation verwendet werden kann. Da das Register eine Division der Eingangsfolge durch das Generatorpolynom durchführt, bildet der verbleibende Inhalt einen Bezug zum Ergebnis der Division, nämlich deren Rest.
Beispiel 2: Bestimmung der Signatur zu einer Eingabefolge
Für das Signaturregister von Bsp. 1 soll die Signatur bestimmt werden, die aus der Eingabefolge (von links nach rechts)
0 1 0 1 0 1 0 1 0 1 0 1 0 0 1 0
nach 16 Taktschritten entsteht. Eine Reduktion der Information erfolgt hierbei nicht, dies ist aber bei längeren Eingabefolgen der Fall.
Als Lösung bieten sich 2 Wege an: Rückgriff auf die Kodierungstheorie und Berechnen der Signatur durch Division oder schrittweises Bestimmen der Signatur mit Hilfe der Schaltung. Der letztere Weg ist einsichtiger und soll deshalb hier vorgestellt werden.
Der Eingang v entsteht durch die Beziehung (# für antivalent)
v = E # S9 # S7 # S4 # S0
Solange das Register in diesen Stellen nur den Wert 0 enthält, wird der Eingang E in S15 gespeichert und der jeweilige Inhalt um eine Stelle nach rechts geschoben. Im Schritt 8 wird dadurch S9 = 1, so dass durch Schritt 9 diese 1 nach S15 gelangt, da der Eingang 0 ist. Gleichzeitig wird S9 wieder 0, so dass bei Schritt 10 wiederum der Eingang allein S15 bestimmt. Nun sind S9 und S7 1, so dass sich ihre Wirkung im Schritt 11 aufhebt. Dies wiederholt sich im Schritt 13, während im Schritt 14 S4 wirksam wird. Insgesamt entsteht im Register die Signatur 6CAA als vierstellige Hexadezimalzahl im Code von Bsp. 1, wie man aus Zeile 16 ablesen kann.
| Schritt | Eingabe | Registerinhalt nach Taktimpuls | ||||||||||||||||
| i | E | V | S15 | S14 | S13 | S12 | S11 | S10 | S9 | S8 | S7 | S6 | S5 | S4 | S3 | S2 | S1 | S0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 14 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 16 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
Der andere Weg betrachtet die Signalfolgen als Polynome, so dass im vorliegenden Fall bei Zählung mit abnehmenden Potenzen bei zunehmenden Zeitpunkten
(x14 + x12 + 10 + x8 + x6 + x4 + x):(x16 + x9 + x7 + x4 + 1)
zu dividieren ist. Es lässt sich leicht zeigen, dass nach 16 Divisionsschritten der Quotient
q = x-2 + x-4 + x-6 + x-8 + x-9 + x-10 + x-12 + x-14 + x-15
in das Register geschoben wird. Der höchstwertige Koeffizient steht dabei am weitesten rechts, so dass die Anzeige aus dem Spiegelpolynom des Quotienten q*(x) = x-1q(1/x) in der Form
q* = x14 + x13 + x11 + x9 + x8 + x7 + x5 + x3 + x
entsteht, der dem obigen Ergebnis entspricht /3, 4/.
Das folgende Beispiel erläutert die Erzeugung der fehlerfreien Signaturen nach dem angegebenen Verfahren für ein kleines Schaltwerk, das aus zwei D-Flipflops mit Taktpegelsteuerung und asynchroner Voreinstellung sowie einem Schaltnetz zur Ansteuerung besteht.
Beispiel 3: Schaltung mit Signaturen im fehlerfreien Fall
Gegeben sei das folgende Schaltwerk mit der zugehörigen Zustandsübergangstabelle für die ebenfalls vorgegebene Folge der 4 Eingangssignale und Takt T bei S für ¬S oder S invertiert:
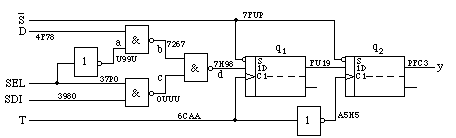
| i | S | D | SEL | SDI | T | a | b | c | d | q1 | q2=y |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 5 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 6 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 8 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 9 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 10 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 11 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 12 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 14 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 15 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 16 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
Zur Interpretation der Tabelle ist zunächst zu bemerken, dass die 4 Eingangssignale (ohne T) über die Zwischenvariablen a, b, c den zukünftigen Wert der D-Flipflops bestimmen. Jede Zeile enthält die Information für die Zustandsübergänge, indem die neuen Zustände nach dem Takt und dieser nach der Stabilisierung der anderen 4 Eingänge angegeben sind. D.h. in Zeile 1: S setzt unbedingt die Flipflops auf q1q2 = 11. In Zeile 2 ist S inaktiv, während D, SEL, SDI über das Schaltnetz d = 0 erzeugen. T = 1 überträgt diesen Wert nach q1, wobei q2 unverändert bleibt. In Zeile 3 wird wegen T = 0 nur q2 verändert, alles Übrige bleibt konstant.
Wie man durch Probieren feststellen kann, erlauben die angegebenen Eingangssignale die Erkennung aller Einzelfehler st 0 und st 1 des Schaltwerks. Diese deterministische Testfolge beeinflusst entsprechend die Signaturen. Sie sind für den fehlerfreien Fall in die Schaltung eingetragen. Ihre Bestimmung wurde bereits in Bsp. 2 erläutert. Man beachte, dass die dort benutzte Eingangsfolge E der Spalte für T entspricht. Folglich trägt die Taktleitung die zugehörige Signatur 6CAA.
Hat man auf diese Weise alle Signaturen im fehlerfreien Fall erzeugt und dabei eine Testfolge als Eingangssignale verwendet, ist zu erwarten, dass sich alle auftretenden Fehler in abweichenden Signaturen auswirken, so dass deren Vergleich mit dem fehlerfreien Fall eine einfachere Diagnose mit Benutzerführung (guided probing) erlaubt. Dazu wird bei abweichender Ausgangssignatur stufenweise jeder vorangehende Knoten abgetastet und die Signatur mit der Sollsignatur verglichen. Ein Fehler ist lokalisiert, wenn entweder ein Baustein oder eine Leitung gefunden ist, bei denen die Ausgangssignatur fehlerhaft, alle Eingangssignaturen aber fehlerfrei sind. Für bestückte Leiterplatten als Prüfobjekt ist die Diagnosemethode unmittelbar verwendbar, da hier alle Signalknoten zugänglich sind. Das nachfolgende Beispiel erläutert die zu erwartende Fehlerauswirkung.
Beispiel 4: Fehlerauswirkung auf die Signaturen
Für die Schaltung in Bsp. 3 wird als Fehler angenommen, dass die Verbindung c unterbrochen ist. Der zugehörige NAND-Ausgang wird dann die fehlerfreie Signatur aufweisen, während für den Eingang der nachfolgenden Stufe bei TTL-Technologie eine Einsfolge wirksam wird. Nach Bsp. 2 läßt sich dafür die Signatur FP7U herleiten, die am Eingang der nachfolgenden Stufe meßbar ist, wenn die Unterbrechung auf der Leiterplatte erfolgt, nicht aber im Baustein, (der als gleichwertigen Fehler einen offenen Eingang aufweisen könnte). Weitere Schritte nach Bsp. 2 bestätigen die Fehlersignaturen d = CF18, q = PP99 und y = 8UC3, während alle übrigen Signaturen mit Bsp. 3 übereinstimmen. Dies ist in das nachfolgende Bild eingetragen.
Da für c der Anfang der Leitung eine korrekte, das Ende eine falsche Signatur aufweisen, ist durch Betrachtung der Signaturen der Fehler lokalisiert.
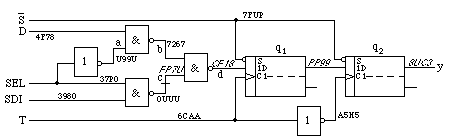
Soweit sollte deutlich geworden sein, dass die Signaturanalyse eine Hilfe bei der Fehlerlokalisierung darstellt, wobei auch Schaltwerke behandelt werden können. Allerdings ist die Schaltung von Bsp. 3 sehr einfach, indem globale Zustandsrückkopplungen fehlen, also eine Auswirkung der Zustandsgrößen auf die Signale in den Schaltnetzbereichen nicht eintreten kann. Um diese Situation auch bei allgemeinen Schaltwerken zu erreichen, werden Möglichkeiten vorgesehen, in einem Testmodus die Rückkopplungen aufzutrennen, z.B. durch zusätzliche Schaltelemente, die als Testhilfe aufgefasst werden lönnen. Da dies ebenfalls einen Eingriff in die Schaltung darstellt, soll hier nicht näher darauf eingegangen werden. Es sei nur darauf hingewiesen, daß damit die Signaturanalyse ganz allgemein auf Schaltwerke angewendet werden kann, um deren Fehlerdiagnose zu erleichtern.
Rückgekoppelte Schieberegister lassen sich auch zur Erzeugung von Pseudozufallsfolgen verwenden, die ihrerseits als Testmuster verwendbar sind. So liefert Bsp. 1 bei Eingabe Null und einem von Null verschiedenen Anfangswert eine Zustandsfolge des Registers, die sich erst nach 216 - 1 Schritten wiederholt, also alle Zustände durchläuft. Man spricht von Pseudozufallsfolgen, weil eigentlich eine kausale Steuerung des Zustandsablaufs vorliegt, die aber in den einzelnen Registerstellen wegen der langen Periode wie eine binäre Zufallsfolge aussieht. Es ist leicht einzusehen, dass bei genügend langen Zufallsfolgen und aufgetrennten Rückkopplungen die Wahrscheinlichkeit recht hoch ist, dass jeder Signalknoten beide logische Werte annimmt und im Fehlerfall eine Abweichung am Schaltungsausgang produziert, der sich in einer veränderten Signatur äußert. Der Nachweis hierfür ist jedoch nicht ganz einfach und kann aus Platzgründen hier nicht durchgeführt werden.
Literatur
- Frohwerk, R.A. Signature analysis, Hewlett-Packard J. 28, Nr. 9, 1977, p. 2...8
- Bennetts, R.G. Design of testable logic circuits, Addison Wesley, London, 1984
- Leisengang, D. Signaturanalyse in der Datenverarbeitung - Anwendungen und Beispiele, Elektronik 21, 21.10.1983, S. 67...72
- Peterson, W.W. Error-correcting codes, 2. ed., Weldon, E.J. MIT Press, Cambridge, Mass, 1988
[Hinweise]
[Englisch] [Deutsch] [Russisch]
Letzte Änderung: 7. April, 2004