Introduction
Capacitor units (CU) are widely used in industry for wattles power compensation.
Voltage unsinusidality is distortion of the voltage curve, which has the sinusal form. Voltage unsinusidality reduses worktime of the CU and increases the true power loses. So that, unsinusidality influence on CU research is relevant for practice.
Relevance of the topic
Practical relevance is conditioned by the wide spread of the capacitor units and the scientific is conditioned on the fact that till the present time electromagnetic compatibility was estimated only for CU model without the series links, in spite of their quantity can reach 16. Given algorithm of the items in polynomial forming allows getting the transmissive functions with any quantity of the series RC-circuits in the CU model, that are necessary for analytic solution of the electromacnetic compabilityof the CU estimation task. Moreover, there are no data about CU computer models in literature, although they are necessary for such purpose like correctness of analytic solution tests, electromagnetic compability of the CU estimation in cases when there is no analytic solution.
Purpose of the work
The purpose is estimation of the capacitor units’ electromagnetic compatibility with the help of mathematical and computer modeling.
Content of the work
Voltage uy unsinusidality in the greatest extent makes an influence to the capacitor units, increasing their current iCv, power loses and decreasing their service term. For it’s turn, the CU connection decreases unsinusidality level. For analysis of the unsinusidality’s influence on CU consequences it is necessary to have a mathematical description (model) of the unit. In literature there is used the substitution scheme which is given on the picture.
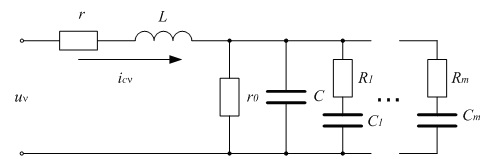
Picture 1 – Capacitor unit substitution scheme
Here r and L – conductor’s ohmic resistance and inductance, r0 и С – ohmic resistance and capacity, R1, …, Rm and C1, …, Cm – relaxator’s ohmic resistance and capacity, that are modeling the dependence of tangent delta from frequency. In the work an ohmic resistance rм and inductance Lм of circuit are added to this scheme, so that the model characteristics are changed significantly.
Modern capacitor units have the isolation with the practically constant tangent delta, so that relaxators in model become useless. Taking into account, that r + Rм<< r0, we can write the transmissive function of system in this form:
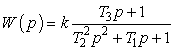 ,
,where k = zCH/r0 – transmission coefficient, zCH – nominal full resistance of CU, T1 = L/r0+(r+Lм)·C, T22 = LC, T3 = r0C.
Having changed operator p for jω, we can get an amplitude-frequency function of system:
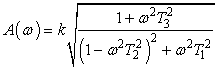 ,
,Also the transmissive function was found, that is correspond exponentially-cosine process.
Analysis shows that the line resistance and inductance are significantly exceed similar characteristics of CU conductors, so that we can accept that L ≈ 0 and r ≈ 0. Line’s characteristics depend of its length. This entails amplitude and resonance maximum frequency changing. In practice it is important to analyze dependence of the frequency and transmissive functions in frequency range up to 2000 Hz, i.e up to ω = 4000π rad/sec.
Model allows estimating an influence of unsinusidality of any form (transmissive, random) on CU.
Literature
- Введение в статическую динамику систем электроснабжения/ Шидловский А.К., Куренный Э.Г. – Киев: Наукова думка, 1984. – 273с.
- Электромагнитная совместимость электроприемников промышленных предприятий/ Под ред. А.К. Шидловского. – Киев: Наукова думка, 1992. – 236 с.
- Ермилов А. А. Основы электроснабжения промышленных предприятий. – М.: Энергоатомиздат, 1983.
- Жежеленко И. В., Саенко Ю. Л. Показатели качества электроэнергии и их контроль на промышленных предприятиях. – М.: Энергоатомиздат, 2000.
- Ермуратский В.В., Ермуратский П.В. Конденсаторы переменного тока в тиристорных преобразователях. – М.: Энергия, 1979. – 224 с.
- Тимофеев Д.В. Упрощенные вероятностные методы расчета несимметричных и несинусоидальных режимов в электрических системах с однофазными тяговыми нагрузками//Электричество. – 1963. – №9. – с. 48–54.
- Комлев В.П., Малафеев С.И. Динамическая модель силового конденсатора и ее применение для расчета потерь при искажениях напряжения. – Владимир, 1982. – 12 с. – Деп. в Информэнерго 29.11.82, №1196эн – Д82.
