Вступ
Конденсаторні установки (КУ) широко застосовуються в промисловості для компенсації реактивної потужності.
Несінусоідальність напруги – це викривлення кривої напруги, що має сінусоідальну форму. Несінусоідальність напруги зменшує строк служби КУ і збільшує втрати активної потужності. Тому дослідження впливу несинусоідальності на КУ актуально для практики.
Актуальність
Практична актуальність зумовлена широким розповсюдженням КУ, а наукова – тим, що до цього часу ЕМС оцінювалась виключно для моделі КУ без серієсних ланок, незважаючи на те, що у загальному випадку їх кількість сягає 16. Запропонований алгоритм формування доданків у многочленах дозволяє отримати передаточні функції за будь-якої кількості сірієсних RC-ланцюгів в моделі КУ, необхідні для аналітичного рішення задачі оцінювання ЕМС КУ. Більш того, у літературі відсутні дані про комп’ютерні моделі КУ, хоч вони і потрібні для таких цілей: перевірка правильності аналітичних рішень, оцінювання ЕМСК У в випадках, коли аналітичне рішення відсутнє.
Мета роботи
Метою роботи є оцінка ЕМС конденсаторних установок шляхом математичного і комп’ютерного моделювання.
Зміст роботи
Несінусоїдальність напруги uy у найбільшій мірі впливає на конденсаторні установки (КУ), збільшуючи їх струм iCv, втрати потужності і скорочуючи строк служби. В свою чергу, підключення КУ зменшує рівень несінусоідальності. Для аналізу наслідків впливу несінусоідальності на КУ потрібно мати математичний опис (модель) установки. В літературі використовується заступна схема КУ, яку представлено на рисунку.
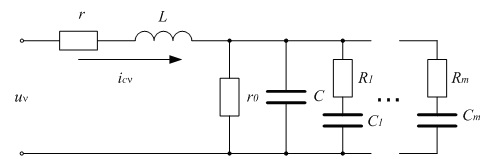
Рисунок 1 – Схема заміщення конденсаторної установки
Тут r і L – активний опір і індуктивність провідників КУ, r0 и С – активний опір і ємність КУ, R1, …, Rm і C1, …, Cm – активні опори і ємності релаксаторів, які моделюють залежність тангенса дельта від частоти. В роботі до цієї схеми додається активний опір rм і індуктивність Lм мережі, що значно змінює параметри моделі.
Сучасні КУ мають ізоляцію с практично постійним тангенсом дельта, тому релаксатори в моделі стають зайвими. Враховуючи, що r + Rм<< r0, передавальну функцію системи запишемо у вигляді
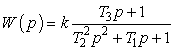 ,
,де k = zCH/r0 – коефіцієнт передачі, zCH – номінальний повний опір КУ, T1 = L/r0+(r+Lм)·C, T22 = LC, T3 = r0C.
Замінивши оператор p на jω, отримаємо амплітудно-частотну функцію системи:
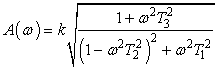 ,
,Знайдено також перехідну функцію, яка представляє собою експоненціально-косінусоідальний процесс.
Аналіз показує, що опір і індуктивність лінії значно перевищують аналогічні параметри провідників КУ, тому можна приймати L ≈ 0 і r ≈ 0. Параметри лінії залежать від її довжини. Це призводить до зміни амплітуди і частоти резонансного максимуму. Для практики важливо проаналізувати залежність частотної і перехідної функції у діапазоні частот до 2000 Гц (згідно ГОСТ 13109-97), тобто до ω = 4000π рад/с.
Модель дозволяє оцінити вплив несінусоідальності будь-якої форми (перехідної, випадкової) на КУ.
Література
- Введение в статическую динамику систем электроснабжения/ Шидловский А.К., Куренный Э.Г. – Киев: Наукова думка, 1984. – 273с.
- Электромагнитная совместимость электроприемников промышленных предприятий/ Под ред. А.К. Шидловского. – Киев: Наукова думка, 1992. – 236 с.
- Ермилов А. А. Основы электроснабжения промышленных предприятий. – М.: Энергоатомиздат, 1983.
- Жежеленко И. В., Саенко Ю. Л. Показатели качества электроэнергии и их контроль на промышленных предприятиях. – М.: Энергоатомиздат, 2000.
- Ермуратский В.В., Ермуратский П.В. Конденсаторы переменного тока в тиристорных преобразователях. – М.: Энергия, 1979. – 224 с.
- Тимофеев Д.В. Упрощенные вероятностные методы расчета несимметричных и несинусоидальных режимов в электрических системах с однофазными тяговыми нагрузками//Электричество. – 1963. – №9. – с. 48–54.
- Комлев В.П., Малафеев С.И. Динамическая модель силового конденсатора и ее применение для расчета потерь при искажениях напряжения. – Владимир, 1982. – 12 с. – Деп. в Информэнерго 29.11.82, №1196эн – Д82.
