Введение
Конденсаторные установки (КУ) широко используются в промышленности для компенсации реактивной мощности.
Несинусоидальность напряжения – это искажение кривой напряжения, которая имеет синусоидальную форму. Несинусоидальность напряжения уменьшает срок работы КУ и увеличивает потери активной мощности. Поэтому исследование влияния несинусоидальности на КУ актуально для практики.
Актуальность
Практическая актуальность обусловлена широким распространением КУ, а научная – тем, что до настоящего времени ЭМС оценивалась исключительно для модели КУ без сериесных звеньев, несмотря на то, что в об щем случае их количество достигает 16. Предложенный алгоритм формирования слагаемых в многочленах позволяет получить передаточные функции при любом количестве сериесных RC-цепей в модели КУ, необходимых для аналитического решения задачи оценивания ЭМС КУ. Более того, в литературе отсутствуют данные о компьютерных моделях КУ, хотя они и нужны для таких целей: проверка правильности аналитических решений, оценивания ЭМС КУ в случаях, когда аналитическое решение отстутствует.
Цель работы
Целью работы является оценка ЭМС конденсаторных установок путем математического и компьютерного моделирования.
Содержание работы
Несинусоидальность напряжения uy в наибольшей мере влияет на конденсаторне установки (КУ), увеличивая их ток iCv, потери мощности и сокращая срок службы. В свою очередь, подключение КУ уменьшает урівень несинусоидальности. Для анализа последствий влияния несинусоидальности на КУ не обходимо кметь математическое описание (модель) установки. В литературе используется схема замещения КУ, которая представлена на рисунке.
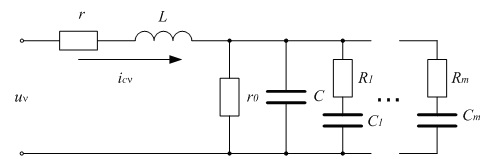
Рисунок 1 – Схема замещения конденсаторной установки
Здесь r и L – активное сопротивление и индуктивность проводников КУ, r0 и С – активное сопротивление и емкость КУ, R1, …, Rm и C1, …, Cm – активне сопротивления и емкости релаксаторов, которые моделируют зависимость тангенса дельта от частоты. В работе к этой схеме прибавляется активное сопротивление rм и индуктивность Lм сети, что значительно менует параметры модели.
Современные КУ имеют изоляцию с практически постоянным тангенсом дельта, поэтому релаксаторы в модели становятся лишними. Учитывая, что r + Rм<< r0, запишем передаточную функцію системы в виде
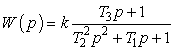 ,
,где k = zCH/r0 – коэффициент передачи, zCH – номинальное полное сопротивление КУ, T1 = L/r0+(r+Lм)·C, T22 = LC, T3 = r0C.
Заменив оператор p на jω, получаем амплитудно-частотную функцію системы:
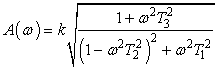 ,
,Также была найдена переходная функція, представляющая собой экспоненциально-косинусоидальный процесс.
Анализ показывает, что сопротивление и индуктивность линии значительно превышают аналогичные параметры проводников КУ, поэтому можно принять L ≈ 0 и r ≈ 0. Параметры линии зависят от ее длины. Это приводит к изменению амплитуды и частоты резонансного максимума. Для практики важно проанализировать зависимость частотной и переходной функцій в диапазоне частот до 2000 Гц (согласно ГОСТ 13109-97), т.е. до ω = 4000π рад/с.
Модель позволяет оценить влияние несинусоидальности любой формы (переходной, случайной) на КУ.
Литература
- Введение в статическую динамику систем электроснабжения/ Шидловский А.К., Куренный Э.Г. – Киев: Наукова думка, 1984. – 273с.
- Электромагнитная совместимость электроприемников промышленных предприятий/ Под ред. А.К. Шидловского. – Киев: Наукова думка, 1992. – 236 с.
- Ермилов А. А. Основы электроснабжения промышленных предприятий. – М.: Энергоатомиздат, 1983.
- Жежеленко И. В., Саенко Ю. Л. Показатели качества электроэнергии и их контроль на промышленных предприятиях. – М.: Энергоатомиздат, 2000.
- Ермуратский В.В., Ермуратский П.В. Конденсаторы переменного тока в тиристорных преобразователях. – М.: Энергия, 1979. – 224 с.
- Тимофеев Д.В. Упрощенные вероятностные методы расчета несимметричных и несинусоидальных режимов в электрических системах с однофазными тяговыми нагрузками//Электричество. – 1963. – №9. – с. 48–54.
- Комлев В.П., Малафеев С.И. Динамическая модель силового конденсатора и ее применение для расчета потерь при искажениях напряжения. – Владимир, 1982. – 12 с. – Деп. в Информэнерго 29.11.82, №1196эн – Д82.
