Введение
Машины точечной контактной сварки (МТКС) имеют широкое распространение в промышленности. Однако существует ряд проблем, связанных с проектировкой сетей питания МТКС, а так же их эксплуатацией. Благодаря тому, что эти машины имеют малое значение коэффициента включения и большие нагрузки, то в случаи одновременного включения, они создают в электрических сетях значительные пиковые нагрузки и колебания напряжения. Следовательно, питающая сеть должна удовлетворять двум условиям: 1) допустимого нагрева; 2) допустимой потери напряжения.
Обеспечение на выводах любой включенной машины номинального напряжения, является ключевым условием, так как оказывает главное влияние на технологический процесс и качество сварки. Зависимость качества сварки от уровня напряжения показана на рисунке 1.

Рисунок 1 – Зависимость усилий разрыва точек от напряжения при точечной сварке изделий из стали 08кп при толщине деталей 0,8 + 0,8 мм (а), 1 + 1 мм (б), 1,5 + 1,5 (в), 2,5 + 2,5 мм (г)
Актуальность данной разработки связана с интенсивным применением МТКС, что приводит к необходимости использования более точных методик расчета потерь напряжения и пиковых токов, так как существующие методы основываются на приблизительных расчетах. Применение более точного метода приведет к уменьшению капитальных затрат на питающую сеть.
Цель работы – разработка более точного метода расчета потерь напряжения и пиковых токов для разветвленной сети, питающей группу машин точечной контактной сварки, с целью снижения капитальных затрат на сеть при обеспечении требуемого уровня напряжения в сети
Обзор литературных источников
Развитие теории нагрузок было положено в работах Тихонова В.П., Каялова Г.М., Лившица Д.С., Мукосеева Ю.Л. и др. В них было предложено два метода определения расчетных нагрузок: статистический метод [1] и метод упорядоченных диаграмм [2]. Оба этих метода основывались на теоретическом анализе графиков нагрузки с помощью вероятностных кривых распределения, а так же на обработке данных, полученных опытным путем в заводских сетях.
Во “Временных руководящих указаниях по определению электрических нагрузок промышленных предприятий”, выпущенных в 1961 г., за основу был взят метод упорядоченных диаграмм. На сегодняшний день действующие указания по расчет нагрузок [3], основываются на модифицированном статистическом методе [4]. Стоит заметить, что метод упорядоченных диаграмм и модифицированный статистический не могут применяться для машин контактной сварки, так как они создают не равномерный график нагрузки. Кроме того необходимо рассчитывать потерю напряжения в сетях питания и определять пиковые нагрузки.
Способы определения величины пиковых нагрузок и их продолжительности были описаны в методе вероятностного моделирования графика нагрузки Каялова Г.М. [5], а затем развиты в работах Куренного Э.Г. Так же над этим вопросом работали Штейнике Г.А. [6] и Вагин Г.Я. [7].
В работе Мухи В.П. [8], был предложен метод определения отклонения напряжения на зажимах МТКС и расчета пиковых нагрузок в сети питания машин точечно контактной сварки с заданной вероятностью.
Кроме методов аналитического расчета электрических нагрузок разработаны методики статистического моделирования [9].
Теоретическое обоснование аналитического метода расчета максимальных токов и потерь напряжения в сети питания МТКС
Для определения пиковых нагрузок в Указаниях [15], а так же в работе Мухи В.П. [8], применяется двухступенчатая максимальная модель, в которой максимальный пик тока определяется по суммарной нагрузке машин, время работы которых совпало с определенной вероятностью.
При условно зафиксированном числе одновременно включенных машин т их суммарный импульс тока Im является случайной величиной. Распределение этой величины определяется совокупностью разных наборов индивидуальных импульсов Ir и коэффициентов включения kвr отдельных машин в заданной группе.
Согласно общему принципу максимальной модели [10] расчет вероятного максимума Ix = Im.max = F(ex) заменен более простым. Эта модель заменяет заданную группу машин эквивалентной ей с тем же числом машин, но только с двумя значениями импульсов тока.
В основу двухступенчатой диаграммы положена упорядоченная векторная диаграмма (УД) нагрузок машин. Она учитывает импульсы Ir и длительность включения kвr. Такую модель получают путем приведения упорядоченной диаграммы к простейшей форме, учитывающей импульсы двух видов: от n1 машин с наибольшим импульсом и (n - n1) с наименьшим расчетным импульсом.
Значение основного параметра модели определяется условием равенства ее площади и площади исходной УД:
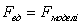
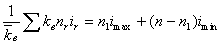
где:
 .
.
Рисунок 2 – Упорядоченная диаграмма токов МТКС и ее двухступенчатая модель
Величина расчетного пика определяется по формуле:
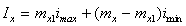
где mx1 – расчетное количество одновременно работающих машин с наибольшим индивидуальным импульсом (рис.3);
mx – находится по рисунку 3 в зависимости от
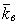 и n
и n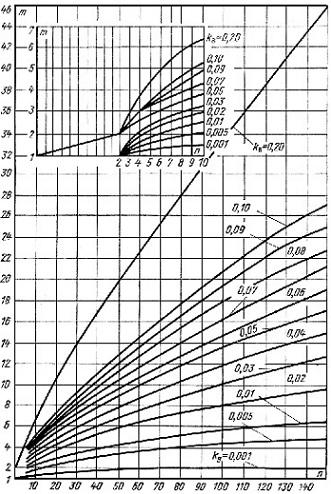
Рисунок 3 – Зависимость расчетного максимума mx числа одновременно включенных машин от их общего количества n при разных значениях
Определение максимальной потери напряжения основано на методе фиктивных нагрузок, в соответствии с которым суммарная потеря напряжения в сети в любой момент времени обусловливается числом совпавших в работе машин и потерями напряжения, создаваемыми работой каждой машины.
Поскольку потеря напряжения в сети от работы одной машины пропорциональна ее токовой нагрузке, ее можно рассматривать как фиктивную нагрузку этой машины. Это позволяет вести расчет суммарной максимальной потери напряжения аналогично расчету пиковой токовой нагрузке.
Потеря напряжения, вызываемая каждой отдельной машиной:

где
 –
коэффициент, учитывающий
суммарные
потери напряжения в питающих линиях от нагрузок различных фаз машин
(таб. 1);
–
коэффициент, учитывающий
суммарные
потери напряжения в питающих линиях от нагрузок различных фаз машин
(таб. 1);Таблица 1 – Значение
коэффициента  для
сварочных машин.
для
сварочных машин.
| Тип машины | Расчетные фазы | ||
| AB | BC | CA | |
| однофазные | |||
| AB | 2 | 0,5 | 0,5 |
| BC | 0,5 | 2 | 0,5 |
| CA | 0,5 | 0,5 | 2 |
| двухфазные | |||
| AB,BC | 2,4 | 2,4 | 1,73 |
| AB,CA | 2,4 | 1,73 | 2,4 |
| BC,CA | 1,73 | 2,4 | 2,4 |
| трехфазные | |||
| ABC | 1,73 | 1,73 | 1,73 |
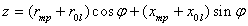
де rтр, xтр – активное и реактивное сопротивление трансформатора, r0l, x0l – активное и реактивное сопротивление участка электрической сети от источника питания до МТКС.
Усредненная потеря напряжения от отдельной сварочной машины:
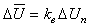
Усредненная потеря напряжения в питающей сети от группы машин:
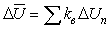
Средний коэффициент включения фиктивных нагрузок одинаков для всех междуфазных напряжений, поскольку он определяется для всех машин группы независимо от их распределения по фазам (и по мощности):

Из равенства площадей упорядоченной диаграммы и ее двухступенчатой модели находится количество сварочных машин, создающих максимальную потерю напряжения

откуда
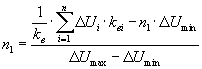
Расчетная потеря напряжения определяется по формуле:
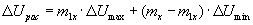
Здесь ΔUmax, ΔUmin – максимальное и минимальное значение потери напряжения. Величины mx и mx1 находятся аналогично расчету пикового тока, рассмотренного выше.
Метод "Граничных функций распределения пиковых токов и потерь напряжения"
Методика расчета, положенная в основу действующим Указаний [2], опирается на применение двухступенчатой модели упорядоченной диаграммы сварочных токов МТКС, что приводит к погрешности и создает определенный запас при выборе питающей сети и, как следствие, увеличивает капитальные затраты на нее.
Точное решение задачи можно получить только для небольшого числа сварочных машин в группе путем перебора всех возможных вариантов одновременно включенных МТКС, расчета вероятностей совпадений токов, напряжений в сети и построения по полученным данным функций распределения пиковых токов и потерь напряжения.
Однако на практике это возможно только при небольшом количестве сварочных машин из-за большого количества вариантов включения, что значительно увеличивает объем расчетов. Так как реальное количество машин может достигать сотен, точный расчет в этом случае становится невозможным. Для уменьшения объема расчетов предложен метод “Граничных функций распределения” [11], позволяющий определить участки, необходимые для нахождения расчетных максимальных значений, предельных функций распределения искомых величин для каждой фазы. Эти функции распределения дают возможность найти диапазон максимальных расчетных значений потерь напряжения и пиковых токов. В методе “Граничных функций распределения” для уменьшения числа ступеней функций распределения все сварочные машины были разбиты на 7 групп в зависимости от количества фаз и того, к каким фазам подключена машина:
- однофазные, подключенные к фазам AB; BC; CA;
- двухфазные, подключенные к фазам AB, BC; BC, CA; CA, AB;
- трехфазные.
При расчете функций распределения рассматриваются все возможные комбинации включения разного количества машин из групп. Максимальные функции распределения получаем, выбирая из каждой группы требуемое число включенных СМ наибольшей мощности, минимальные – наименьшей. В методе используется алгоритм точного расчета токов и напряжений, как и при расчете точной функции распределения для небольшого числа МТКС.
Метод "Случайного выбора"
Очевидно, что по расчетным значениям потерь напряжения, определенным по минимальным функциям распределения, нельзя выбрать питающую сеть, а использование максимальных функций распределения будет вносить определенный запас, поскольку во всех вариантах одновременного включения сварочных машин из групп выбираются только самые мощные машины.
Для получения более достоверных результатов разработан новый метод “Случайного выбора” [12], основанный на методе “Граничных функций распределения”. В нем, так же как и в методе “Граничных функций распределения”, все сварочные машины делятся на 7 групп, а отличие состоит в том, что при расчете функций распределения включенные сварочные машины из каждой группы выбираются случайным образом. После рассмотрения всех возможных вариантов, строятся функции распределения, по которым определяются расчетные максимальные значения пиковых токов и потерь напряжения.
Метод “Случайного выбора” будет усовершенствован путем учета фактических значений коэффициентов включения сварочных машин при случайном выборе включенных машин из группы. В существующей версии метода вероятности включения машин одинаковы, а в модифицированной – они будут зависеть от их коэффициентов включения. Вторым способом повышения точности метода “Случайного выбора” является расчет нескольких функций распределения одной и той же величины с последующим осреднением расчетных значений, определенных по каждой из них.
Другие методы расчета
В [13,14] предлагается вести расчет пиковых нагрузок, как и нагрузок по нагреву, по полной мощности. Заранее распределяют одно- и двухфазные МТКC в трехфазной сети. Условия и порядок такого распределения приведен в [10].
Нахождение расчетной пиковой нагрузки ведется по наиболее загруженному плечу трехфазной сети. При этом нагрузку каждой однофазной и двухфазной машины приводят к нагрузке трехфазной

где
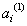 – коэффициент приведения, равный: 2 – для
однофазных машин,
которые подключают на напряжение расчетного плеча; 0,5 – для
однофазных МТКС, которые включают на два других межфазных напряжения.
– коэффициент приведения, равный: 2 – для
однофазных машин,
которые подключают на напряжение расчетного плеча; 0,5 – для
однофазных МТКС, которые включают на два других межфазных напряжения.
Для двухфазных МТКС применяют одну из формул
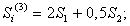
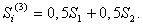
Первая – если двухфазная
машина включается только
одним
плечом на расчетное напряжение; вторая – если не включается
ни одним плечом. Если  ,
соответственно получается:
,
соответственно получается:
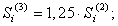

Условием такого приведения является равенство падения напряжения в трехфазной сети, которое образуют одно- или двухфазные МТКС и приведенная трехфазная машина.
Для преодоления трудностей
дальнейшего расчета, группа
трехфазных и
приведенных до них машин заменяются одной машиной с максимальной
мощностью 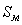 и условным
и условным  количеством СМ с одинаковой условной мощностью
количеством СМ с одинаковой условной мощностью 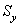 каждой машины.
Величины
каждой машины.
Величины  и
и 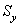 определяются по формулам:
определяются по формулам:
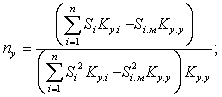
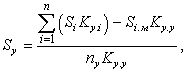
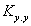 – условный
коэффициент включения одной машины после замены, равный
среднему значению коэффициентов
– условный
коэффициент включения одной машины после замены, равный
среднему значению коэффициентов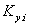 всех МТКC.
всех МТКC.
Так как потери напряжения во время
пиковых нагрузок
пропорциональны
величинам этих нагрузок, методы расчета вероятностных потерь напряжения
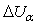 аналогичны методам
расчета вероятностных пиковых нагрузок, приведенных
выше.
аналогичны методам
расчета вероятностных пиковых нагрузок, приведенных
выше.
Порядок расчета 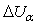 следующий:
следующий:
- Для каждой i-ой машины рассчитывают величину потери напряжения, полученной на тех участках сети до расчетной СМ, по которым протекает мощность і-ой машины.
- Рассчитывают условную величину группового коэффициента включения Ky.y., который принимают равным среднему значению индивидуальных Ky.і.;
- Выбирают
расчетную машину с максимальной потерей
напряжения. Другие
(n-1) СМ с
разными Ky.і.
и ΔUі
заменяют условным количеством nу
машин с одинаковыми Ky.y.
и ΔUі.у;
величины Ky.і.
и
ΔUі
рассчитывают по формулам, аналогичным
тем, по которым
рассчитывались пиковые нагрузки: в них полные мощности заменяют на
соответствующие потери напряжения:
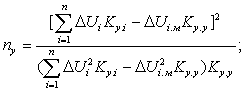

- Находят величину эквивалентных
перекрытий х
на интервале
времени
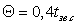 , где
, где 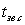 –
среднее значение времени сварки для всех СМ, по вероятностным кривым
–
среднее значение времени сварки для всех СМ, по вероятностным кривым  .
На рис. 4, 5 приведены вероятностные кривые для
.
На рис. 4, 5 приведены вероятностные кривые для  и
и 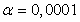 соответственно.
соответственно. - Находят величину
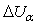 по
выражению
по
выражению
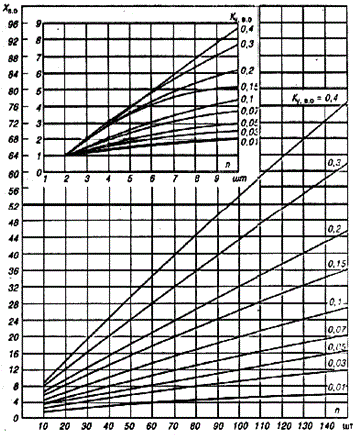
Рисунок 4 – Кривые
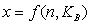 по
по 

Рисунок 5 – Кривые
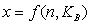 по
по 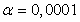
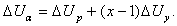
В дальнейшем планируется на основе предложенных методов разработать универсальную методику, позволяющую рассчитывать разветвленные сети и сети с двухсторонним питанием машин точечной контактной сварки, провести сравнение разработанных методов с методами, предлагаемыми в [13,14].
Литература
- Каялов Г.М. Определение расчетных нагрузок промышленных электрических сетей по методу упорядоченных диаграмм нагрузок // Материалы научно-технического совещания по определению электрических нагрузок и регулированию напряжения промышленных предприятий. Госэнергоатомиздат, 1958, вып.3. – C. 14–16
- Мешель Б.С. Применение математической статистики для определения электрических нагрузок промышленных предприятий. Энергосбыт Киевэнерго, Киев, 1958. – 128 c.
- Руководящий технический материал. Указания по расчету электрических нагрузок: РТМ 36.18.32.4 – 92: Утв. ВНИПИ Тяжпромэлектропроект: Введен с 01.01.93 // Инструктивные и информационные материалы по проектированию электроустановок. – М.: ВНИПИ Тяжпромэлектропроект. – 1992. – № 6-7. – C. 4–27
- Жохов Б.Д. Анализ причин завышения расчетных нагрузок и возможной их коррекции // Промышленная энергетика. – 1989. – №7. – C. 17–21
- Каялов Г.М. Принцип максимума средней нагрузки в расчетах электрических сетей. ИВУЗ, Электромеханика, 1964. – №3. – c.8–11
- Штейнике Г.А. Применение теории вероятностей и математической статистики для определения электрических нагрузок точечных машин контактной сварки. Труды Горьковского политехнического института, 1961, т.XVII, вып. 2
- Вагин Г.Я. Исследование режимов работы и расчет пиковых нагрузок машин контактной электросварки. //Электрические сети и системы, Межведомственный республиканский научно-технический сборник, 1970, вып.7. – C. 8–10
- Муха В.П. Вопросы теории и расчета электрических нагрузок и потерь напряжения в сетях контактной электросварки. // Диссертация на соискание ученой степени к.т.н. Ростовский-на-Дону институт инженеров железнодорожного транспорта, 1975. – 204 c.
- Мукосеев Ю.Л., Вагин Г.Я., Червонный Е.М. Расчет суммарной нагрузки машин контактной сварки методом статистического моделирования на ЦВМ. // Электричество. 1972, – №6. – C. 1–9
- Вагин Г.Я. Режимы электросварочных машин. – М.: Энергия, 1975. – 189 c.
- Воротніков С.О. Розрахунок напруг у електричній мережі, від якої живляться машини контактної зварки. Кваліфікаційна робота магістра – Донецьк, ДонНТУ, 2009. – 100 с.
- Болотнов Д.В. Розрахунок максимальних струмів і втрат напруги в електричних мережах живлення машин контактної електричної зварки. Кваліфікаційна робота магістра – Донецьк, ДонНТУ, 2010. – 100 с.
- Денисенко М.А Розрахунок пікових навантажень,що створюють установки для контактного електрозварювання в електричних мережах //Промелектро (Інформаційний збірник). – 2009. – №4. – C. 8–18
- Денисенко М.А Розрахунок втрат напруги в електричних мережах, що живлять установки для контактного електрозварювання //Промелектро(Інформаційний збірник). – 2009. – №5. – C. 31–40
- Теоретические основы аналитического метода максимальных токов и потерь напряжения в сетях контактной электросварки. / Г.М. Каялов, В.П. Муха, А.А. Бадахян, Л.Б. Годгельф // Инструктивные указания по проектированию электротехнических промышленных установок. – Москва.: ГПИ Тяжпромэлектропроект. – 1976. – №3. – С. 3–9


