Актуальность научная и практическая
Динамические погрешности трансформаторов тока и их коррекция
Динамические погрешности первичных преобразователей параметров режима
Введение
Измерительный трансформатор тока – трансформатор, предназначенный для преобразования тока до значения, удобного для измерения. Первичная обмотка трансформатора тока включается последовательно в цепь с измеряемым переменным током, а во вторичную включаются измерительные приборы. Ток, протекающий по вторичной обмотке трансформатора тока, пропорционален току, протекающему в его первичной обмотке.
Трансформаторы тока широко используются для измерения электрического тока и в устройствах релейной защиты электроэнергетических систем, в связи с чем на них накладываются высокие требования по точности. Трансформаторы тока обеспечивают безопасность измерений, изолируя измерительные цепи от первичной цепи с высоким напряжением, часто составляющим сотни киловольт.
Вторичные обмотки трансформатора тока обязательно нагружаются. Сопротивление нагрузки строго регламентировано требованиями к точности коэффициента трансформации. Незначительное отклонение сопротивления вторичной цепи от номинала приводит к изменению погрешности преобразования и возможно ухудшению измерительных качеств трансформатора. Значительное увеличение сопротивления нагрузки создает высокое напряжение во вторичной обмотке, достаточное для пробоя изоляции трансформатора, что приводит к выходу трансформатора из строя, а также создает угрозу жизни обслуживающего персонала.
Практическая актуальность заключается в оценке погрешностей вносимых измерительным трансформатором. В паспортных данных для измерительного трансформатора указывается класс точности, что позволяет оценить погрешности в статических режимах при неизменном или медленно изменяющихся нагрузках. При оценке несинусоидальности и колебания тока необходимо оценивать динамические погрешности.
Научная актуальность заключается в разработке метода оценки погрешности и ее коррекции.
Научное положение: предложен метод синтеза процесса изменения первичного тока, новизна которого заключается в использовании динамической модели измерительного трансформатора для определения динамической погрешности и ее коррекции.
Динамические погрешности трансформаторов тока и их коррекция
Измерительные трансформаторы работают в области линейных характеристик системы «первичный ток i1 – вторичный ток i2», поэтому процессы в них описываются линейными дифференциальными уравнениями. Для краткости ограничимся уравнением первого порядка.
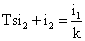
где s – оператор Лапласа, k – коэффициент трансформации, Т – постоянная времени трансформатора и измерительной цепи. В этом случае имеем передаточную функцию.
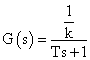
амплитудно – частотную функцию. (АЧФ)
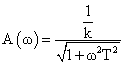
фазочастотную функцию (ФЧФ)
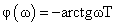
где ω – угловая частота измеряемого синусоидального сигнала.
Постоянная времени может быть найдена опытным путем или расчетным – по схеме замещения трансформатора. При отсутствии сведений ее можно ориентировочно оценить по допустимой угловой погрешности Δφ, которая приводится в каталогах при ω1=100π рад/с и измеряется в угловых минутах.
Приравняв (ФЧФ) к Δφ, получим:
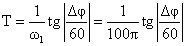
где учтено, что угловая минута в 60 раз больше одного радиана.
Например, для трансформаторов с классом точности 0,2; 0,5 и 1% нормируются значения погрешностей ±10°, ±40° и ±80°. Учитывая, что угловая секунда в 60 раз превышает один радиан, согласно получим искомые значения постоянной времени: 9,3; 37 и 74мкс
На рис.1 приведены АЧФ для этих значений постоянной времени, где через f=ω ⁄ 2π обозначена частота измеряемого сигнала: А1(f), А2(f) и А3(f) – для Т=9,3; 37 и 74 мкс.
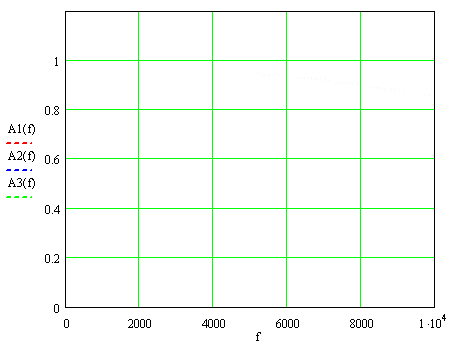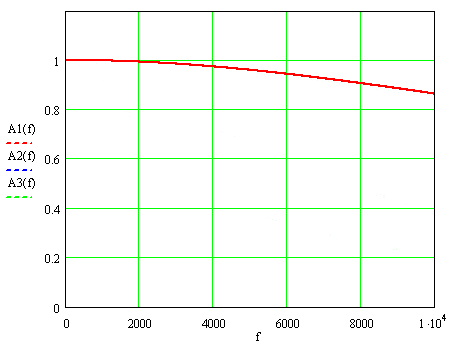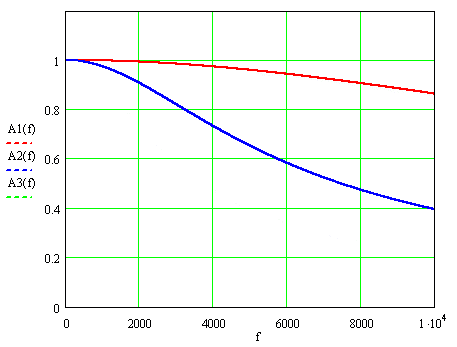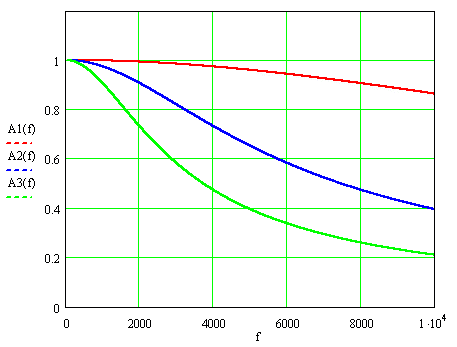
Рисунок 1. Амплитудно - частотные функции трансформаторов тока.
При номинальной частоте 50 Гц АЧФ, умноженная на k, практически не отличается от единицы: 0,999996, 0,99993 и 0,99973, в то время при наибольшей частоте 2000 Гц учитываемых гармоник отличия более существенны: 0,993, 0,907 и 0,732.
Для получения искомого неискаженного процесса достаточно к каждой ординате процесса i2(t) прибавить корректирующий множитель Ti'2. Коррекцию можно выполнить в темпе реального времени, добавив в измерительную цепь форсирующее звено первого порядка с параметром Т. Погрешность коррекции определяется точностью дифференцирования. Если записанный график тока аппроксимируется дифференцируемой функцией, то погрешность отсутствует. Для иллюстрации в табл.1 приведены данные об амплитудах I2 и фазах ψ2 гармоник тока дугового замыкания на землю в сети 6 кВ с изолированной нейтралью, который измерялся с использованием трансформатора тока с классом точности 1%.
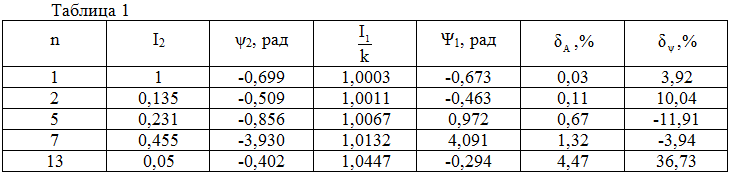
Токи выражались в относительных единицах относительно амплитуды первой гармоники. Значения частотных характеристик рассчитывались при T=7.4·10-5 c.
Скорректированные параметры гармоник:
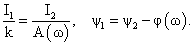
Относительные погрешности измерения амплитуд и фаз гармоник в процентах
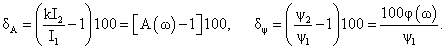
При исследовании случайных процессов, для которых понятие гармоники теряет смысл, погрешности статистических характеристик оцениваются по спектральной плотности записанного процесса или по его корреляционной функции – с использованием переходной функции трансформатора
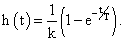
Динамические погрешности первичных преобразователей параметров режима
Также в системах автоматизации технологических объектов для контроля параметров режима используются первичные преобразователи (ПП).
Каждый ПП представляют собой динамическую систему, линейную в рабочем диапазоне. Поэтому процесс .gif) на выходе
ПП отличается от фактического y(t). Динамическая погрешность зависит как от параметров ПП, так и вида процесса, регистрируется. Целью работы
является оценка погрешностей и их коррекция.
на выходе
ПП отличается от фактического y(t). Динамическая погрешность зависит как от параметров ПП, так и вида процесса, регистрируется. Целью работы
является оценка погрешностей и их коррекция.
ПП моделируется звеном второго порядка с постоянными времени T1 и T2 либо первого порядка с постоянной времени T. В последнем случае можно использовать все результаты для звена второго порядка, положив в них T1=T и T2=0.
Процессы в ПП описываются дифференциальным уравнением
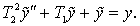
Амплитудная и фазовая частотные функции (АЧФ и ФЧФ) имеют вид
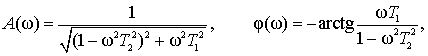
где ω – угловая частота.
Разницу в процессах наглядно видно на примере, когда измеряется единичная функция, а T1<2T2.
Обозначив через 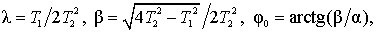 , получим процесс
, получим процесс
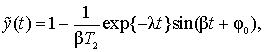
Который не только отличается от единицы, но имеет и колебательную составляющую. Если процесс является периодическим, то он представляется в виде ряда Фурье. Пусть гармоника порядка n с основной угловой частотой ω1 имеет амплитуду cn и фазу φn. Параметры гармоники, которые рассчитаны по процессу, будут другими:
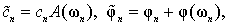
Поскольку при ω=0 АЧФ равен единице, а ФЧФ - нулю, то среднее значение yc определяется без погрешности.
Для периодического процесса
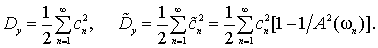
Непериодический процесс описывается спектральной плотностью S(ω) в диапазоне частот ω от 0 до бесконечности.
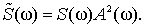
Интегрирования этой плотности дает дисперсию
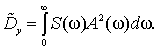
Например, для случайного процесса с плотностью
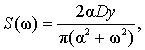
которая имеет параметр α, интегрирование дает
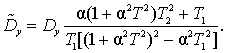
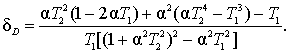
Как видно, относительная погрешность не зависит от дисперсии процесса, а определяется через параметр α и постоянные времени ПП.
На рисунке 2 приведены зависимости погрешностей дисперсий для постоянных времени.
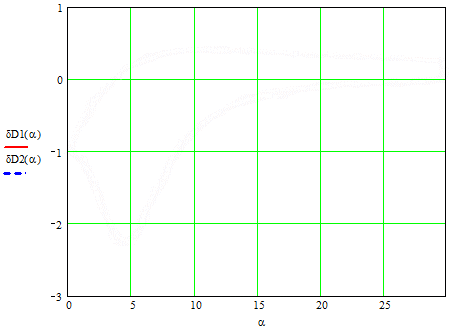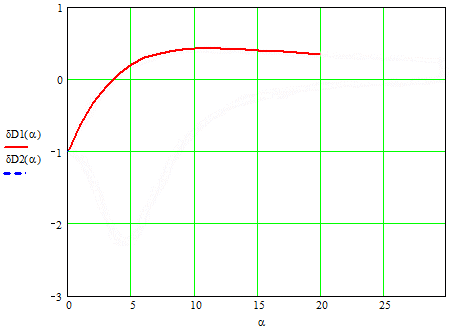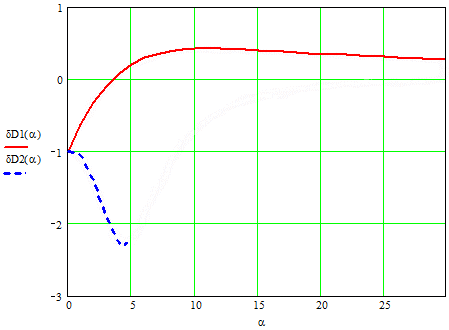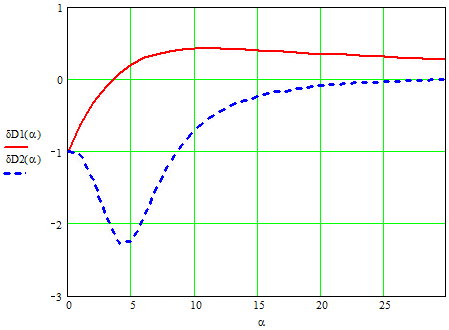
Рисунок 2 Зависимости погрешностей дисперсий от α
Перейдем к методам коррекции динамической погрешности. Известным здесь является процесс .gif) , по
которому надо восстановить фактический процесс y(t). Точность восстановления зависит от расчета производных.
, по
которому надо восстановить фактический процесс y(t). Точность восстановления зависит от расчета производных.
Реальные процессы .gif) не имеют разрывов, поэтому в некоторых случаях их можно
аппроксимировать аналитическими выражениями, дифференцируются. Тогда процесс отстраивается без погрешностей.
не имеют разрывов, поэтому в некоторых случаях их можно
аппроксимировать аналитическими выражениями, дифференцируются. Тогда процесс отстраивается без погрешностей.
Конечно процессы .gif) задаются в виде последовательности ординат с малым шагом дискретности времени.
Использование компьютерных операторов дифференцирования обеспечивает достаточную точность восстановления процесса y(t).
задаются в виде последовательности ординат с малым шагом дискретности времени.
Использование компьютерных операторов дифференцирования обеспечивает достаточную точность восстановления процесса y(t).
Периодический процесс может будет отстроенным и по гармоника:
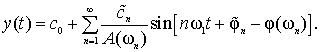
В этом случае дифференцировки не нужно, но возникает известная проблема с определением амплитуд и фаз гармоник, а также количества гармоник, которые нужно учитывать. Таким образом, коррекция динамических погрешностей позволяет значительно уменьшить требования к динамическим характеристикам первичных преобразователей параметров режима.
Выводы
Выводы будут сформулированы после проведения опытов.
Литература
1. Бессонов Л.А. Теоретические основы электротехники. Изд. 6-е, перераб. И доп. Учебник для студентов энергетических и электротехнических вузов. М., «Высшая школа», 1973. 752с.
2. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Наука, 1989. 301с.
3. Электрические измерения // Под ред. В.Н. Малиновского. – М.: Энергоатомиздат, 1985.416с.
4. Теория автоматического управления // под ред. А.А. Воронова. - М.: Высшая школа, 1977, ч.1. - С. 303.
5. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969. - С.576.
6. Ермилов А.А. Основы электроснабжения промышленных предприятий. – М.: Энергоатомиздат, 1983. – 208 с
7. Трансформаторы тока / В.В. Афанасьев, Н.М. Адоньев, Л.В. Жалалис и др. – Л.:Энергия, 1980
8. Справочник по электроизмерительным приборам; Под ред. К. К. Илюнина — Л.:Энергоатомиздат, 1983


