Актуальність научна та практична
Динамічні похибки трансформаторів струму та їх корекція
Динамічні похибки первинних перетворювачів параметрів режиму
Вступ
Вимірювальний трансформатор струму - трансформатор, який призначений для перетворення струму до значення, зручного для виміру. Первинна обмотка трансформатора струму включається послідовно в ланцюг з вимірюваним змінним струмом, а у вторинну включаються вимірювальні прилади. Струм, що протікає по вторинній обмотці трансформатора струму, пропорційний струму, що протікає в його первинній обмотці.
Трансформатори струму широко використовуються для вимірювання електричного струму і в пристроях релейного захисту електроенергетичних систем, у зв'язку з чим на них накладаються високі вимоги по точності. Трансформатори струму забезпечують безпеку вимірювань, ізолюючи вимірювальні ланцюги від первинної ланцюга з високою напругою, часто складовим сотні кіловольт.
Вторинні обмотки трансформатора струму обов'язково навантажуються. Опір навантаження строго регламентовано вимогами до точності коефіцієнта трансформації. Незначне відхилення опору вторинної ланцюга від номіналу призводить до зміни похибки перетворення і можливо погіршення вимірювальних якостей трансформатора. Значне збільшення опору навантаження створює високу напругу у вторинній обмотці, достатню для пробою ізоляції трансформатора, що призводить до виходу трансформатора з ладу, а також створює загрозу життю обслуговуючого персоналу.
Практична актуальність полягає в оцінці похибок внесених вимірювальним трансформатором. У паспортних даних для вимірювального трансформатора вказується клас точності, що дозволяє оцінити похибки в статичних режимах при незмінному або повільно змінюються навантаженнях. При оцінці несинусоїдальності і коливання струму необхідно оцінювати динамічні похибки.
Наукова актуальність полягає в розробці методу оцінки похибки та її корекції.
Наукове положення: запропоновано метод синтезу процесу зміни первинного струму, новизна якого полягає у використанні динамічної моделі вимірювального трансформатора для визначення динамічної похибки та її корекції.
Динамічні похибки трансформаторів струму та їх корекція
Вимірювальні трансформатори працюють в області лінійних характеристик системи «первинний струм i1 – вторинний струм i2», тому процеси в них описуються лінійними диференціальними рівняннями. Для стислості обмежимося рівнянням першого порядку.
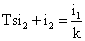
де s - оператор Лапласа, k - коефіцієнт трансформації, Т - постійна часу трансформатора та вимірювального ланцюга. У цьому випадку маємо передавальну функцію.
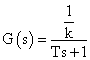
амплітудно - частотну функцію. (АЧФ)
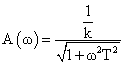
фазочастотную функцію (ФЧФ)
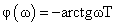
де ω – кутова частота вимірюваного синусоїдального сигналу.
Постійна часу може бути знайдена дослідним шляхом чи розрахунковим - за схемою заміщення трансформатора. При відсутності відомостей її можна орієнтовно оцінити за припустимою кутовий похибки Δφ, яка наводиться в каталогах при ω1=100π рад/с і вимірюється в кутових хвилинах.
Прирівнявши (ФЧФ) до Δφ, отримаємо:
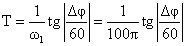
де враховано, що кутова хвилина в 60 разів більше одного радіан.
Наприклад, для трансформаторів з класом точності 0,2; 0,5 і 1% нормуються значення похибок ±10°, ±40° и ±80°. Враховуючи, що кутова секунда в 60 разів перевищує один радіан, згідно отримаємо шукані значення постійної часу: 9,3; 37 і 74мкс
На рис.1 наведено АЧФ для цих значень постійної часу, де через f=ω ⁄ 2π позначена частота вимірюваного сигналу: А1(f), А2(f) и А3(f) – для Т=9,3; 37 и 74 мкс.
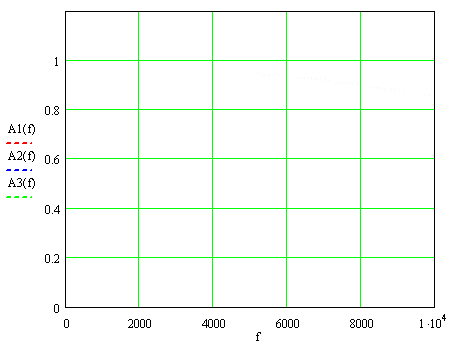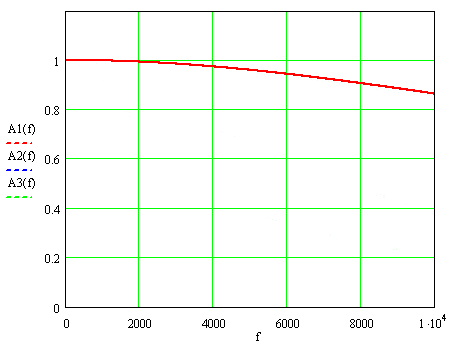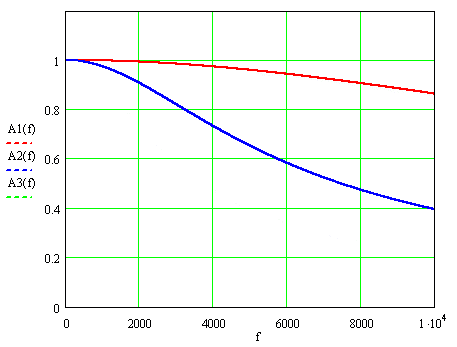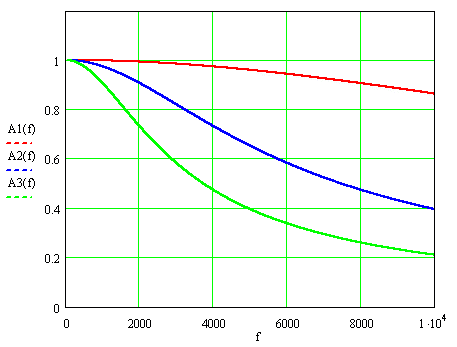
Рисунок 1. Амплітудно - частотні функції трансформаторів струму.
При номінальній частоті 50 Гц АЧФ, помножена на k, практично не відрізняється від одиниці: 0,999996, 0,99993 і 0,99973, в той час при найбільшої частоті 2000 Гц враховуються гармонік відмінності більш істотні: 0,993, 0,907 і 0,732.
Для отримання потрібного неспотвореного процесу досить до кожної ординаті процесу i2(t) додати коригувальний множник Ti'2. Корекцію можна виконати в темпі реального часу, додавши в вимірювальный ланцюг форсовану ланку першого порядку з параметром Т. Похибка корекції визначається точністю диференціювання. Якщо записаний графік струму апроксимується диференційовною функцією, то похибка відсутня. Для ілюстрації у табл.1 наведені дані про амплітудах I2 та фазах ψ2 гармонік струму дугового замикання на землю в мережі 6 кВ з ізольованою нейтраллю, який вимірювався з використанням трансформатора струму з класом точності 1%.
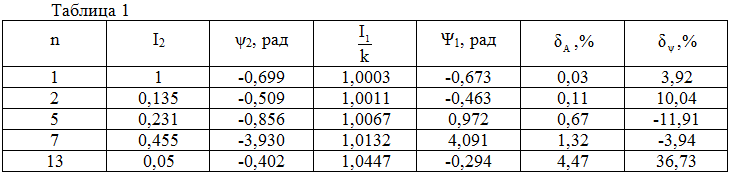
Струми виражалися у відносних одиницях щодо амплітуди першої гармоніки. Значення частотних характеристик розраховувалися при T=7.4·10-5 c.
Скориговані параметри гармонік:
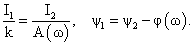
Відносні похибки вимірювання амплітуд і фаз гармонік у відсотках
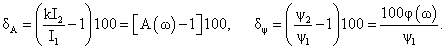
При дослідженні випадкових процесів, для яких поняття гармоніки втрачає сенс, похибки статистичних характеристик оцінюються по спектральної щільності записаного процесу або за його кореляційної функції - з використанням перехідної функції трансформатора
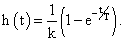
Динамічні похибки первинних перетворювачів параметрів режиму
Також в системах автоматизації технологічних об'єктів для контролю параметрів режиму використовуються первинні перетворювачі (ПП).
Кожен ПП представляють собою динамічну систему, лінійну в робочому діапазоні. Тому процес .gif) на виході
ПП відрізняється від фактичного y(t). Динамічна похибка залежить як від параметрів ПП, так і виду процесу, реєструється. Метою роботи
є оцінка похибок і їх корекція.
на виході
ПП відрізняється від фактичного y(t). Динамічна похибка залежить як від параметрів ПП, так і виду процесу, реєструється. Метою роботи
є оцінка похибок і їх корекція.
ПП моделюється ланкою другого порядку з постійними часу T1 та T2 або першого порядку з постійною часу T. В останньому випадку можна використовувати всі результати для ланки другого порядку, поклавши в них T1=T та T2=0.
Процеси в ПП описуються диференціальним рівнянням
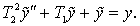
Амплітудна і фазова частотні функції (АЧФ і ФЧФ) мають вигляд
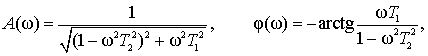
где ω – кутова частота.
Різницю в процесах наочно видно на прикладі, коли вимірюється одинична функція, а T1<2T2.
Позначивши через 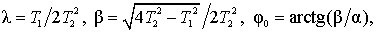 , отримаємо процес
, отримаємо процес
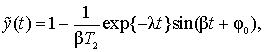
Який не тільки відрізняється від одиниці, але має і коливальну складову. Якщо процес є періодичним, то він представляється у вигляді ряду Фур'є. Нехай гармоніка порядку n з основною кутовий частотою ω1 має амплітуду cn і фазу φn. Параметри гармоніки, які розраховані по процесу, будуть іншими:
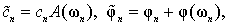
Оскільки при ω=0 АЧФ дорівнює одиниці, а ФЧФ - нулю, то середнє значення yc визначається без похибки.
Для періодичного процесу
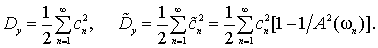
Неперіодичний процес описується спектральною щільністю S(ω) в діапазоні частот ω від 0 до нескінченності.
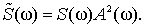
Інтегрування цієї щільності дає дисперсію
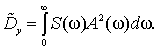
Наприклад, для випадкового процесу з щільністю
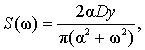
яка має параметр α, інтегрування дає
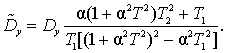
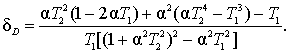
Як видно, відносна похибка не залежить від дисперсії процесу, а визначається через параметр α і постійні часу ПП.
На рисунку 2 приведені залежності похибок дисперсій для постійних часу.
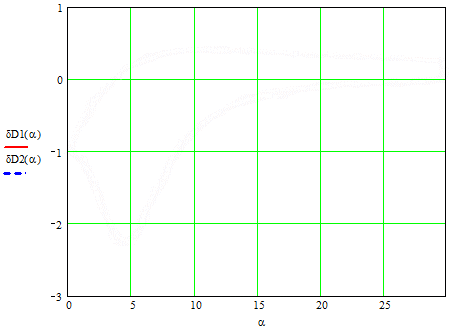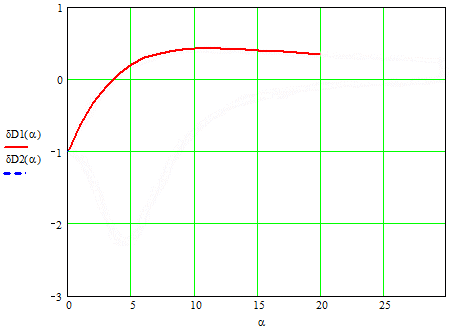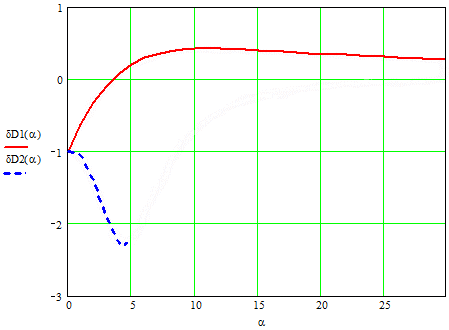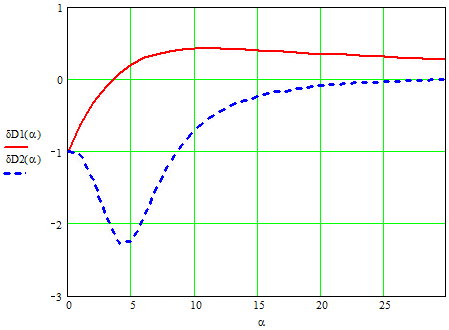
Рисунок 2 Залежності похибок дисперсій від α
Перейдемо до методів корекції динамічної похибки. Відомим тут є процес .gif) , по
якого треба відновити фактичний процес y(t). Точність відновлення залежить від розрахунку похідних.
, по
якого треба відновити фактичний процес y(t). Точність відновлення залежить від розрахунку похідних.
Реальні процеси .gif) не мають розривів, тому в деяких випадках їх можна
апроксимувати аналітичними виразами, диференціюються. Тоді процес відбудовується без похибок.
не мають розривів, тому в деяких випадках їх можна
апроксимувати аналітичними виразами, диференціюються. Тоді процес відбудовується без похибок.
Звичайно процеси .gif) задаются в виде последовательности ординат с малым шагом дискретности времени.
Использование компьютерных операторов дифференцирования обеспечивает достаточную точность восстановления процесса y(t).
задаются в виде последовательности ординат с малым шагом дискретности времени.
Использование компьютерных операторов дифференцирования обеспечивает достаточную точность восстановления процесса y(t).
Періодичний процес може буде відбудованим і по гармоніка:
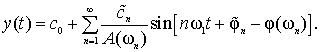
У цьому випадку диференціювання не потрібно, але виникає відома проблема з визначенням амплітуд і фаз гармонік, а також кількості гармонік, які потрібно враховувати. Таким чином, корекція динамічних похибок дозволяє значно зменшити вимоги до динамічних характеристик первинних перетворювачів параметрів режиму.
Висновки
Висновки будуть сформульовані після проведення дослідів.
Литература
1. Бессонов Л.А. Теоретические основы электротехники. Изд. 6-е, перераб. И доп. Учебник для студентов энергетических и электротехнических вузов. М., «Высшая школа», 1973. 752с.
2. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Наука, 1989. 301с.
3. Электрические измерения // Под ред. В.Н. Малиновского. – М.: Энергоатомиздат, 1985.416с.
4. Теория автоматического управления // под ред. А.А. Воронова. - М.: Высшая школа, 1977, ч.1. - С. 303.
5. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969. - С.576.
6. Ермилов А.А. Основы электроснабжения промышленных предприятий. – М.: Энергоатомиздат, 1983. – 208 с
7. Трансформаторы тока / В.В. Афанасьев, Н.М. Адоньев, Л.В. Жалалис и др. – Л.:Энергия, 1980
8. Справочник по электроизмерительным приборам; Под ред. К. К. Илюнина — Л.:Энергоатомиздат, 1983


