РЕФЕРАТ ПО ТЕМЕ ВЫПУСКНОЙ РАБОТЫ
Содержание:
Содержание:
1. Актуальность темы
2. Анализ публикаций
3. Цель и задачи исследования
4. Физическая модель резонатора с ответвлением
5. Математическая модель нового гидравлического вибрационного контура
Выводы
Список литературы
1. Актуальность темы
Дальнейшее развитие и технический уровень гидроаппаратов неразрывно связан с улучшением их динамических характеристик. Применение существующих гидроаппаратов в технологических машинах, не позволяет обеспечить постоянную надежность работы гидропривода вцелом.
Известными недостатками гидроаппаратов с клапанными или золотниковыми распределительными элементами являются наличие гидродинамических сил, нелинейного трения, возможность гидростатического защемления.
Одним из эффективных путей борьбы с отмеченными недостатками
есть применение гидроаппаратов с осцилляцией, которая отмечается в работах Т.М.Башты, Г.А. Никитина, других исследователей. Однако, рабочие процессы, которые происходят в гидроаппаратах с гидравлическим управлением и с гидравлической осцилляцией, не исследованы и не разработан простой и эффективный
гидравлический вибрационный контур.
Гидроагрегаты, которые применяются в промышленности, характеризуются разнообразием элементов, которые входят в их состав, наличием сложных рабочих процессов, которые имеют место в процессе их функционирования. Методы их расчета и проектирования имеют ряд особенностей, из учета которых возможно улучшить их динамические характеристики: комплексного учета при математическом описании гидроаппаратуры нестационарности гидромеханических процессов и характеристик рабочей жидкости, которые изменяются в процессе его функционирования; усовершенствование схемных решений гидроаппаратуры и компоновки его элементов; повышение точности расчета утечек в подвижных элементах гидроаппаратуры; силы трения на осциллирующем золотнике гидрораспределителя, которые повышают точность математической модели гидроаппаратуры.
Учитывая изложенное, считаю тему магистерской работы, направленную на решение научно - практической задачи, связанной с повышением технического уровня гидроагрегатов использованием пульсации давления рабочей жидкости для сообщения осциляционного
движения подвижным элементам гидроаппаратуры является своевременной и актуальной.
К содержанию
2. Анализ публикаций
Методам проектирования резонатора с ответвлением, который до этого
использовался в качестве гасителя, посвящено небольшое количество работ. Да, в [3, 4] приведены их принципиальные схемы и зависимости для определения объема камеры и размеров каналов. В [5] приведена методика проектирования, которая основана на электроаналогии, при использовании которой накладывается ряд ограничений, увязках с размерами резонатора с ответвлением и порою прохождение нестационарных
гидродинамических процессов. Кроме того, использование этой методики требует проведения предыдущих экспериментальных исследований, что значительно усложняет ее использование. В [6] приведенные математические модели резонатора с ответвлением, построенные с использованием метода Эйлера, но в них
отсутствующие рекомендации относительно определения их рациональных, конструктивных и рабочих параметров. Кроме того, использование данных математических моделей является достаточно трудоемким. Более полное отображение этой проблемы нашло в [7], где приведены математические модели таких устройств, построенных с использованием превращений Фурье, которые могут быть использованы при определенные их рациональных, конструктивных и рабочих параметров. Однако в ней больше внимания уделено гасителям пульсаций давления. Следовательно, определение конструктивных и рабочих параметров резонатора с ответвлением на основе проведения всесторонних аналитических исследований является актуальной научно-технической задачей.
К содержанию
3. Цель и задачи исследования
Целью работы является построение математической модели резонатор с ответвлением, анализ влияния его конструктивных и рабочих параметров на коэффициент передачи.
К содержанию
4. Физическая модель резонатор с ответвлением
В цилиндрическом корпусе 3(емкостный элемент) размещен цилиндрический суженный патрубок 2 (инерционный элемент), который через патрубок 1 подключено к магистрали питания (источники пульсаций давления). Реализовано расшатывающий резонансный контур. Патрубок 4 соединяет резонатор с ответвлением с камерой управления гидрораспределителя. Пульсации давления рабочей жидкости поступают в емкость через патрубки 1 и 2. В случае наличия сдвига фаз пульсирующего потока рабочей жидкости и собственной частоты резонатор с ответвлением, происходит усиление пульсаций давления, которое поступает к камере управления гидрораспределителя. Добирая соответствующие емкости, пересечение и длину суженного патрубка 2, можно получить разные коэффициенты усиления.

Рисунок 1 - Схема резонатора с ответвлением: 1 - входной трубопровод; 2 - входной суженный патрубок; 3 - камера нового гидравлического вибрационного контура; 4 - камера гидрораспределителя.
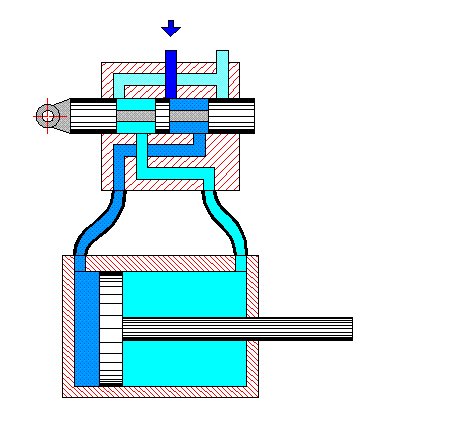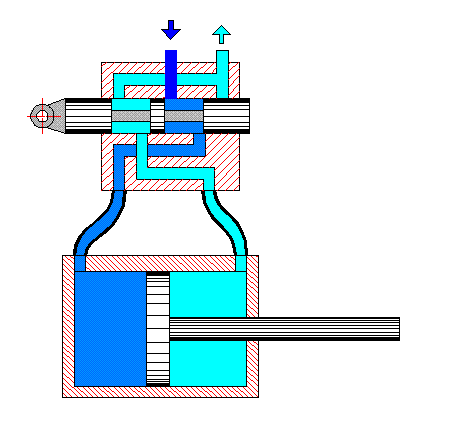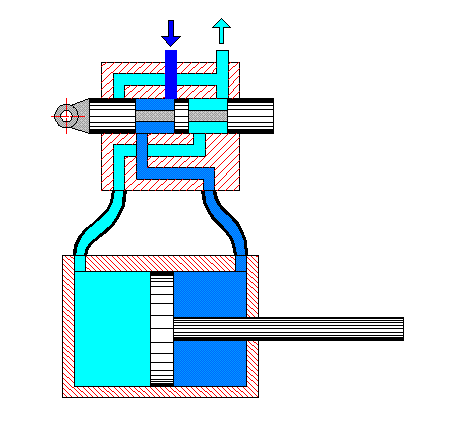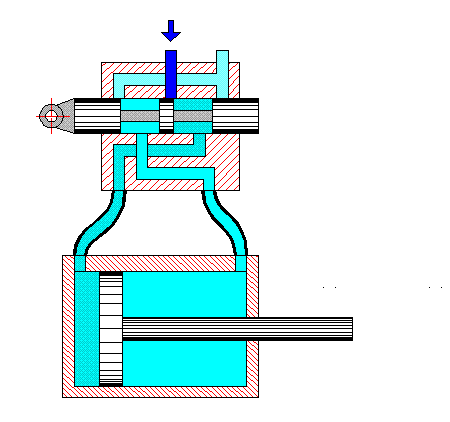
Рисунок 2 – Взаимодействие гидрораспределителя с объемным насосом
(анимация: объем - 244 Кб; размер - 450х422; состоит из 42 кадров; задержка между кадрами - 1с; задержка между последним и первым кадрами - 7с; количество циклов повторения - 25)
К содержанию
5. Математическая модель нового гидравлического вибрационного контура
При составлении математической модели нового гидравлического вибрационного контура сделаем
такие предположения:
- считаем, что в новом гидравлическом вибрационном контуре
происходят устоявшиеся гидродинамические процессы. Не рассматриваем переходные
процессы, связанные с резким изменением параметров на его входе. Рассматриваем
периодические гидродинамические процессы, обусловленные пульсацией давления
рабочей жидкости на выходе из насоса;
- допустим, что профиль распределения скорости рабочей жидкости по сечению каналов нового гидравлического вибрационного контура сформирован;
- считаем, что в гидросистеме, а следовательно и в новом гидравлическом вибрационном контуре,
отсутствует резонанс, кавитация рабочей жидкости и гидравлический удар;
- скорость звука рабочей жидкости является величиной постоянной,
значительно больше от ее скорости в гидросистеме;
- температура рабочей жидкости является постоянной и находится в диапазоне 50-55˚С. Постоянным также есть газосодержимое рабочей жидкости, которое учитывается при расчете модуля объемной упругости рабочей жидкости, который берем постоянным и рассчитываем с учетом упругих
свойств трубопровода;
- уравнение неразрывности рабочей жидкости выполняется на всех
участках гидросистемы;
- массовыми силами рабочей жидкости пренебрегаем. Заметим, что
аналогичное предположение берут большинство исследователей [14, 15];
- рабочую жидкость считаем ньютоновской, а течение изотермической;
- течение рабочей жидкости одномерное осесимметричное.
С учетом принятых предположений, движение рабочей жидкости в гидросистеме может быть
описано с помощью волнового уравнения в виде системы двух дифференциальных уравнений первого порядка,которую с учетом гидравлического сопротивления трубопровода можем записать в виде [8]
 ,(1) ,(1)
где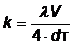 ; λ - коэффициент гидравлического сопротивления; dт - диаметр трубопровода; ρ - плотность рабочей жидкости; V - скорость рабочей жидкости; а - скорость звука в робочей жидкости; р - давление; х - расстояние от начала трубопровода к сечению, где определяется давление (скорость) рабочей жидкости. ; λ - коэффициент гидравлического сопротивления; dт - диаметр трубопровода; ρ - плотность рабочей жидкости; V - скорость рабочей жидкости; а - скорость звука в робочей жидкости; р - давление; х - расстояние от начала трубопровода к сечению, где определяется давление (скорость) рабочей жидкости.
Поскольку затрата через новый гидравлический вибрационный контур отсутствует, членом, который учитывает потери давления в уравнении (1), можно пренебречь. Обоснование этого предположения приведено в [9,10].
Решение (1) будем проводить методом частотного анализа, а именно методом стоячих волн,предложенным Лутцем для расчета волновых процессов. В соответствии с этим методом, решение (1) может быть записано в гиперболичной форме [8].
 ,(2) ,(2)
где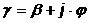 - установившееся распространение волнового процесса; φ - волновое число; l - длина участка трубопровода (канал); - установившееся распространение волнового процесса; φ - волновое число; l - длина участка трубопровода (канал); 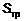 - площадь поперечного сечения трубопровода; - площадь поперечного сечения трубопровода;  - круговая частота колебаний. - круговая частота колебаний.
Задавая предельные условия в виде полного сопротивления (импеданса) Zг
и значение амплитуды скорости и давления в одном перерезе трубопровода с помощью (2), можно найти значение их амплитуд в любом другом сечении. Причем
необходимо также задать предельные условия, которые определяются характером нагрузки на конце трубопровода. А именно наличие затраты в гидросистеме -
дроссели, сопела, насадки и другие. Отсутствие расходов постоянные или переменные объемы на конце заглушенного трубопровода.
Для линейного участка трубопровода при заданном полном сопротивлении нагрузки Zн и приведенном импедансе Z0. Развязок (1) может быть записан в виде [1,2]
 ,(3) ,(3)
где для гидросистемы, в которой отсутствующая расходы рабочей жидкотси:
 ,(4) ,(4)
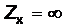 ,(5) ,(5)
С учетом (4) и (5) уравнение (3) приобретет вид
 ,(6) ,(6)
Отметим, что (3) позволяет определить амплитуды давлений и скорости в любой точке гидросистемы и для любых типов нагрузки.
Для гармонических колебаний при 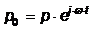 , и , и 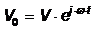 , решение (1) можно также записать в виде (3) [8], где Z0 при отсутствии внутреннего трения определяется из выражения , решение (1) можно также записать в виде (3) [8], где Z0 при отсутствии внутреннего трения определяется из выражения
 , ,
При рассмотрении гидродинамических процессов, которые происходят в новом гидравлическом вибрационном контуре, волны давления распространяются в его каналах с конечной скоростью, какая значительно меньшая скорости звука. Поэтому изменение параметров в любой части нового гидравлического вибрационного контура по времени не успевает повлиять на изменение параметров других частей. Такое
предположение, выходя из физической модели процессов, которые происходят в новом гидравлическом вибрационном контуре, отвечает действительности.
Поскольку все элементы нового гидравлического вибрационного контура являют собой короткие патрубки, считаем, что они все линейны, а предельные условия - постоянны (на входе в новый гидравлический вибрационный контур установились гармонические влияния). При математическом описании гидродинамических процессов в коротких трубопроводах такое предположение принимается большинством исследователей и подтверждено многочисленными экспериментальными исследованиями, например [22]. Тогда структурную схему нового гидравлического вибрационного контура можно представить в виде
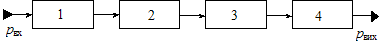
Рисунок 3 - Структурная схема нового гидравлического вибрационного контура: 1 - входной
трубопровод; 2 - входной суженный патрубок; 3 - камера нового гидравлического вибрационного контура; 4 - камера гидрораспределителя.
Для расчета величины давления в любом структурном элементе нового гидравлического вибрационного контура введем коэффициент передачи, под которым будем понимать отношение давления на входе канала (патрубка) к его значению на выходе:
 , ,
Таким образом, (7) позволяет определить, на сколько увеличится (уменьшится) величина давления на выходе
трубопровода в сравнении с его входом. При этом значение коэффициента передачи структурного элемента можем найти из первого уравнения (6).
 ,(8) ,(8)
где
 , ,
Уравнение (7) может быть использовано для расчета коэффициента передачи пульсаций давления, тогда вместо давления входа и выхода него надо подставить амплитуды пульсаций. Если известные коэффициенты передачи отдельных структурных элементов нового гидравлического вибрационного контура и пульсации давления на его входе, можем найти для него коэффициент передачи
НГВК=kп1kп2kп3kп4(9)
Из уравнения (8) и (9) найдем kНГВК, который после представления гиперболичных функций [12], для нового гидравлического вибрационного контура, можем записать в виде
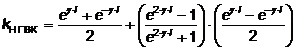 ,(10) ,(10)
где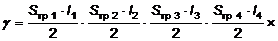
 , ,
Поскольку в новом гидравлическом вибрационном контуре ωосц определяется характеристикой источника питания (насосом) и в общем случае является величиной постоянной, уравнение (10) позволяет, изменяя длину патрубка и величину площади его проходного сечения, выполнить рациональный выбор коэффициента передачи нового гидравлического вибрационного контура. Отметим, что в общем случае его величина должна быть больше 1.[13]
Если известно kНГВК в предположении, изменение давления на выходе из насоса происходит по закону синусоидальным, можем найти пульсации давления в исходной камере нового гидравлического вибрационного контура.
 ,(11) ,(11)
где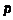 и и 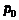 - соответственно пульсации давления в камере нового гидравлического вибрационного контура и амплитуда
пульсаций давления на входе в новый гидравлический вибрационный контура. - соответственно пульсации давления в камере нового гидравлического вибрационного контура и амплитуда
пульсаций давления на входе в новый гидравлический вибрационный контура.
Уравнение (11) является математической моделью нового гидравлического вибрационного контура. Оно позволяет определить силу, которая действует на золотник гидрораспределителя, и параметры его осцилляции. Причем выбор d3 и l3, исходя из того, что за физической сутью входной суженный патрубок и камера 3 нового гидравлического вибрационного контура является резонатором Гельмгольца,
необходимо делать, используя зависимость [8]:
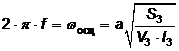 ,(12) ,(12)
где V3- объем камеры 3 нового гидравлического вибрационного контура.
Анализ зависимостей (10) и (12) позволил установить, что с увеличением длины камеры 3 увеличивается и коэффициент передачи нового гидравлического вибрационного контура. Следовательно, длину камеры 3 следует выбирать как можно больше с учетом габаритных ограничений нового гидравлического вибрационного контура.[11]
К содержанию
ВЫВОДЫ
Установлено, что для построения математической модели нового гидравлического вибрационного
контура целесообразно использовать метод спектрального анализа.
С использованием этого метода получена математическая модель нового
гидравлического вибрационного контура.
Проведенные аналитические исследования позволили установить, что наибольшее влияние на
коэффициент передачи имеют диаметры камеры резонатора с отглаженным и зауженым патрубком. Для получения желательных коэффициентов передачи нового гидравлического вибрационного контура длину камеры резонатора с отглаженным следует выбирать как можно больше.
 ,(а) ,(а) ,(б) ,(б)
 ,(в) ,(в) ,(г) ,(г)
 ,(д) ,(д)
Рисунок 4 - Изминение сумарной жёсткости пружины гидрораспределителя с гидравлическим вибрационным контуром в зависимости от перемещения его запорно – регулирующего элемента: а – при изминении амплитуды осциляций; б, в, г, д – для разных типов запорно – регулирующего элемента: 1 – острая дросселирующая кромка, 2 – коническая дросселирующая кромка, 3 - дросселирующая кромка с триугольным заточением, 4 - дросселирующая кромка с заточением в виде сегмента круга, 5 - дросселирующая кромка острая с полукруглой канавкой.
К содержанию
СПИСОК ЛИТЕРАТУРЫ
Андренко П. Н. - Принцип построения гидравлических аппаратов нового класса //Вестник НТУ "ХПИ". - 2001.- Вып. 129. - Ч.2. - С. 102 - 106.
Гречиха И. П. - Математическая модель гидрораспределителя из НГВК //Автоматизация производственных процессов. - 2004. - №2 (19). - С. 16 - 23.
Проектирование и изготовление гидроприводов машин с учетом обеспечения минимального шума. - М.: НИИмаш, 1973. - 55 с.
Kollek W., Kudzma Z., Rutanski J. - Mozliwosci skutecznego tlumienia halasu ukladem filtrow akustycznych // V Konferencja naukowo - tecniczna: Rozwoj budowy eksploatacji I badan maszyn roboczych ciezkich. Zakopane, 1992. - S. 203 - 208.
Шорин В.П. - Устранение колебаний в авиационных трубопроводах. - М.: Машиностроение, 1980. - 156 с.
Андренко П. Н., Клитной В. В., Дмитриенко О. В. - Расчет пульсаций давления на выходе
однокамерного преобразователя пульсаций // Вестник НТУУ КПИ.-1999. - Том 1. -Вып. 36. - С. 87 - 93.
Андренко П. М., Дмитрієнко О. В. Математические модели и расчетные исследования гидравлических гасникі в и усилителей пульсаций давления // Східноєвропейский журнал передовых технологий. - 2004. - № 5 (11). - С. 88 - 93.
Могендович Е. М. Гидравлические импульсные системы. - Л.: Машиностроение, 1977. - 216.
Андренко П. Н., Клитной В. В., Новгородцев В. А. Математическое моделирование течения вязкой жидкости в дросселирующем канале золотникового гидравлического аппарата // Вестник Восточноукраинского национального университета им. В. Даля.- 2002. - №10 (56). - С. 40 - 50.
Скляревский А. Н., Денисенко А. И. Динамика позиционного следящего привода с длинными
гидролиниями // Промышленная гидравлика и пневматика. ‑ 2003.- №1. ‑ С. 47 - 51.
Иванов М. И., Дусанюк С.В., Репінський С.В. - Имитационные исследования волновых процессов в длинных гидравлических линиях гидросистем сельскохозяйственных машин // Вибрации в технике и технологиях. - 2003. - № 4. - С. 69 - 72.
Теория автоматического регулирования. Книга 3. Ч. 1. Теория нестационарных, нелинейных и самонастраивающихся систем автоматического регулирования/Под редакторши В. В. Солодовникова. - М.: Машиностроение, 1969. - 607 с.
Попов Е. П., Пальтов Н. П. - Приближенные методы исследования нелинейных автоматических систем. - М.: Гос. изд. физ.-мат. лит., 1960. - 792 с.
Свешников В.К. Гидрооборудование. Международный справочник. Кн. 3. Вспомогательные элементы гидропривода. - М.: Машиностроение, 2003. - 320 с. [Электронный ресурс]. - Режим доступа: http://engenegr.ru/tehnicheskaya_literatura/gidravlika/20477-gidrooborudovanie-mezhdunarodnyy-spravochnik-v-3-kn-kn-3-vspomogatelnye-elementy-gidroprivoda.htm Коробочкин Б. Л., Комитовски М. Д. О передаточных функциях в гидросистемах в сосредоточенных и распределенных параметрах // Машиностроение. ‑ 1968. ‑ №4. - С. 37 - 44.
К содержанию
|












