
Гридин Дмитрий Александрович
Тема выпускной работы:
Fuzzy-фильтрация для устранения артефактов в регионах интереса в видеопоследовательностях
Научный руководитель: Cамощенко А.В.
Fuzzy-фильтрация в гексагональной решетке
Гридин Д.А., Борисов А.С., Самощенко А.В.Артефакты при сжатии изображений.
Источник: Iнформацiйнi управляючi системи та комп'ютерний монiторiнг (IУС КМ - 2011) : II Всеукраїнська науково-технiчна конференцiя студентiв, аспiрантiв та молодих вчених, 11-13 квiтня 2011 р., м. Донецьк : зб. доп. у 2 т./Донецьк: ДонНТУ, 2011. T.2 - cc. 19-23
Кодирование является неотъемлемой частью процедур сжатия изображения и видео. В частности, дискретное косинусное преобразование (ДКП) – основа алгоритма кодирования изображения JPEG, стандарта кодировки видео MPEG, ITU-T H.263 и пр. [1]. В ходе ДКП входное изображение разбивается на небольшие блоки, как правило размером 8x8, и с использованием матриц квантования преобразуется поблочно в ДКП-коэффициенты. Из квантованных ДКП-коэффициентов формируется поток битов при переменной длине кодирования. На входе декодера полученные данные декодируются, деквантуются и реконструируются по методу обратного ДКП. Такое кодирование допускает присутствие в восстановленных изображениях различных артефактов - блочного (blocking), кольцевого (ringing), москитного (mosquito) и мерцающего (flickering).
Блочные артефакты (рис.1) появляются по причине независимого поблочного преобразования при нарушении корреляции между пикселями на границах блоков. Кольцевые артефакты (рис.2) возникают из-за потери высокочастотных коэффициентов ДКП при квантовании с большим шагом квантования. Кольцевые артефакты являются аналогом эффекта Гиббса и присутствуют в сильно контрастных фрагментах.

а) б)Рис. 1 – Пример блочного артефакта: а) исходное изображение, б) сжатое изображение
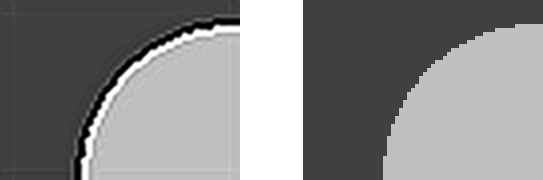
а) б)Рис. 2 – Пример кольцевого артефакта: а) сжатое изображение, б) изображение без кольцевого артефакта
Устранение артефактов в прямоугольной системе координат. Fuzzy-фильтрация
Одним из способов уменьшения наличия перечисленных артефактов в прямоугольной системе координат является использование низкочастотных фильтров [2]. Побочный эффект такого подхода - чрезмерная размытость отфильтрованного изображения. Для решения этой проблемы применяются адаптивные линейные фильтры, однако их реализация требует сложных вычислений.
Для борьбы с блочными и кольцевыми артефактами используется пространственная фильтрация. Нечеткие (fuzzy) фильтры, являющиеся частным случаем bilateral фильтров [3], необходимы для предотвращения размытия при применении линейных фильтров. Цель работы fuzzy-фильтров – устранение артефактов при сохранении четкости контуров изображения.
Предположим, что фильтр h применен по отношению к набору из Ω соседних пикселей x[m+m', n+n'] с центром в x[m,n]:
(1)
В качестве функции зачастую используются функции принадлежности. Например, Гауссова функция принадлежности, которая имеет вид:

Представим ее следующим образом:
(2)
где σ - параметр распространения входных данных, определяющий силу fuzzy-фильтра.
В выражении (1) параметр h(x[m+m',n+n'],x[m,n]) управляет влиянием входных данных x[m+m',n+n'],x[m,n] на результат. Для линейных фильтров h не изменяется и не зависит от исходных данных. В случае нелинейного фильтра, h – функция от входных данных.При этом влияние центрального пикселя x[m,n] на результат всегда выше по сравнению с влиянием других пикселей:
(3)
Для любого выражения |x[m+m’, n+n’] – x[m,n]|, чем выше значение σ, тем большее влияние на результат имеет пиксель x[m+m’,n+n’] по сравнению с центральным – x[m,n]. Меньшие значения σ оставляют сигнал x[m,n] более изолированным от соседних пикселей.[4]
Fuzzy-фильтрация изображений, представленных в гексагональной системеНаиболее распространенным способом вывода изображения на дисплей принято считать его представление в виде набора прямоугольных пикселей, каждому из которых соответствует некоторое значение яркости и цветности. Многочисленные исследования подтверждают эффективность использования гексагональной решетки, в которой каждый пиксель имеет вид шестиугольника [5-7]. Для представления изображения в гексагональной системе может быть использована система координат, изображенная на рис.3. В этом случае координатам обычной системы х и у соответствуют координаты u и v гексагональной системы. Каждой паре координат [x,y] соответствует одна пара координат [u,v], что позволяет с помощью математических преобразований переходить из прямоугольной системы в гексагональную и наоборот.
 Рис. 3 – Гексагональная система координат
Рис. 3 – Гексагональная система координат
Для представления изображения в гексагональной системе координат необходимо выполнить его передискретизацию, т.е. преобразование из обычной прямоугольной системы в гексагональную. Существуют несколько методов для выполнения преобразований. В данном случае использован метод передискритизации, предложенный Вютрихом [8]. Он заключается в создании псевдогексагональных пикселей из кластера квадратных пикселей. Хотя данный метод точно не воссоздает идеальное представление шестиугольника, он позволяет получить форму пикселей, удовлетворяющим основным свойствам гексагональной сетки.
При передискретизации каждый пиксель обычного изображения преобразуется в псевдопиксельный блок размером mxn. В данном случае каждому пикселю обычного изображения соответствует блок размером 13х16, что приводит к получению увеличенного изображения в качестве результата. Аналогично выполнено преобразование обычного изображения в изображение из прямоугольных псевдопикселей размером 9х9. Примеры полученных после передискретизации изображений приведены на рис.4.

а) б)Рис. 4 – Фрагмент изображения с прямоугольными (а) и гексагональными (б) псевдопикселями.
Fuzzy-фильтрация выполняется в гексагональной системе аналогично прямоугольной. Основное отличие заключается в наборах Ω соседних пикселей. В случае обычной системы координат пиксель имеет 8 соседних пикселей, а случае гексагональной - 6 (рис.5). Фрагменты отфильтрованных изображений представлены на рис.6.
![Центральный пиксель [m,n] и соседние пиксели](pic5.jpg)
а) б)Рис. 5 – Центральный пиксель [m,n] и соседние пиксели (а) в прямоугольной и гексагональной (б) системе.

а) б)Рис. 6 – Фрагмент отфильтрованного изображения с прямоугольными (а) и (б) гексагональными псевдопикселями.
Сравнительный анализ результатов фильтрации в прямоугольной и гексагональной системе. Для сравнения fuzzy-фильтрации в рассматриваемых системах координат, над двумя тестовыми изображения выполнены следующие операции. Вначале пиксели исходного зашумленного изображения были преобразованы в прямоугольные и гексагональные псевдопиксели, после чего к полученным изображениям был применен fuzzy-фильтр с параметром распространения σ=10. Затем была восстановлена исходная структура изображений. Результаты фильтрации показаны на рис.7-8.

a) б) в)Рис. 7 – Результаты преобразований. а) исходное зашумленное изображение, б) отфильтрованное в пямоугольной системе, в) отфильтрованное в гексагональной системе

a) б) в)Риc. 8 – Результаты преобразований. а) исходное зашумленное изображение,б) отфильтрованное в прямоугольной системе, в) отфильтрованное в гексагональной системе
Полученные изображения подтверждают работу fuzzy-фильтра. В то же время, визуально достаточно сложно определить разницу между применением фильтра в прямоугольной и гексагональной системе координат. Данная оценка может быть очень субъективной по причине различного восприятия изображений разными людьми. Поэтому для анализа полученных результатов выполнена оценка качества изображений с помощью показателя PSNR (пиковое отношение сигнал-шум). Показатель PSNR для изображения, отфильтрованного в гексагональной системе выше аналогичного показателя для изображения, отфильтрованного в прямоугольной системе на 1-2 дБ. Это означает, что изображение, которое было обработано в гексагональной системе, имеет меньший уровень шума, и, соответственно, фильтрация выполнена более качественно. Показатели PSNR анализируемых изображений приведены в табл.1.
Таблица 1 – Значения PNSR для анализируемых изображений
| PSNR, дб |
| № п/п | Oтфильтровано в прямоугольной системе | Отфильтровано в гексагональной системе |
| 1 | +31.46 | +32.53 |
| 2 | +30.43 | +32.20 |
Экспериментально показано различие в результатах нечеткой фильтрации изображений в прямоугольной и гексагональной системах. Присутствует попытка доказать актуальность применения гексагональной решетки.
Литература- Liu S., Bovik A., Efficient DCT-domain blind measurement and reduction of blocking artifacts, IEEE Trans. Circuits Syst. Video Technol. – v. 12 – no. 12 – 2002 – pp. 1139–1149.
- Nosratinia A., Embedded post-processing for enhancement of compressed images, Proc. IEEE Data Compression Conf. – 1999 – pp. 62–71.
- Chen T., Wu H., Qiu B., Adaptive postfiltering of transform coefficients for the reduction of blocking artifacts IEEE Trans. Circuits Syst. Video Technol. – v. 11 – no. 5 – 2001 – pp. 594–602.
- Vo D. T., Nguyen T. Q., Yea S., Vetro A., Adaptive Fuzzy Filtering for Artifact Reduction in Compressed Images and Videos // IEEE Transactions on Image Processing – v.18 – no.1 – 2009 – Pp. 1166-1178.
- Carstens B. Hexagonal domain transform for shape analysis / B. Carstens, M. Quinn // Intelligent Robots and Computer Vision X: Algorithms and Techniques, SPIE. – v.1607. – 1991. – Pp. 197-205.
- Watson A.B., A hexagonal orthogonal-oriented pyramid as a model of image representation in visual cortex / A.B. Watson, A.J. Ahumada, Jr. // IEEE Biomedical Engineering.– v.36. – no.1. – 1989. – Pp. 97-105.
- Jan W., Conversion of Cartesian coordinates from and to generalized balanced ternary addresses / Jan W. // Photogrammetric Engineering and Remote Sensing, 54. – no. 11. – 1988. – Pp. 1565-1570.
- Wuthrich C.A. An Algorithmic Comparison Between Square-and Hexagonal-based Grid / C.A Wuthrich, P. Stucki // CVGIP: Graphical Models and Image Processing. – Vol. 53 – 1999. – Pp. 324-339.