
Гридин Дмитрий Александрович
Тема выпускной работы:
Fuzzy-фильтрация для устранения артефактов в регионах интереса в видеопоследовательностях
Научный руководитель: Cамощенко А.В.
Реферат по теме «Fuzzy-фильтрация для устранения артефактов в регионах интереса в видеопоследовательностях»
Содержание
Введение
Актуальность темы
Научная значимость работы
Практическая ценность результатов работы
Объект и предмет исследований
Обзор исследований по теме
Основные виды артефактов
Существующие методы по подавлению артефактов
Fuzzy-фильтр
Направленный параметр распространения
Направленный fuzzy-фильтр, основанный на контурах изображения
Заключение
Список литературы
Введение
В цифровой обработке сигналов долгое время исследовались и разрабатывались методы для преобразования звуковых или видео сигналов в цифровую форму. При всяком преобразовании возможны потери, но в то же время пользователи имеют возможности для дополнительных преобразований данных для уменьшения их размера, например для экономии пространства на носителе информации, либо для экономии времени при передаче данных, например через Internet. Естественно, что подобные преобразования не могут выполняться без потерь или искажения данных. В изображениях и видео эти искажения чаще всего выражаются в виде появления нежелательных помех – артефактов.
Актуальность темы
Подавление артефактов для улучшения качества изображения является весьма актуальной задачей, поскольку восстановление поврежденных или зашумленных изображений или видеозаписей в различных ситуациях может быть полезной и ценной операцией.
Научная значимость работы
Научная значимость данной работы заключается в разработке улучшенного метода устранения артефактов в регионах интереса видеопоследовательностей.
Практическая ценность результатов работы
В ходе выполнения работы после проведения моделирования с улучшенным методом устранения артефактов предполагается получить более качественное изображение или видеопоследовательность после обработки исходного искаженного изображения или видео.
Объект и предмет исследований
Объектом исследований является изображение, кадр видеопоследовательности, содержащее различные характерные фрагменты. Предметом исследований являются методы методы фильтрации и обработки изображений.
Обзор исследований по теме
Среди работ магистрантов и сотрудников ДонНТУ тематика восстановления изображений не сильно распространена. Тем не менее имеется большое количетсво интересных работ по обработки изображений различными методами, результаты которых могут быть использованы при рассмотрении исследуемой темы. Некоторые из наиболее интересных работ можно в разделе «Cсылки».
В целом имеется большое число работ по восстановлению изображений и видеопоследовательностей, в том числе и исследуемым методом fuzzy-фильтрации. Зачастую разработанные алгоритмы имеют некоторые схожие черты в методике выполнения фильтрации. Стоит так же заметить, что большинство существующих работ в данном направлении представлены иностранными исследователями.
Основные результаты
Основные виды артефактов
Сигналы, сжатые с помощью блочных алгоритмов, зачастую страдают от различных артефактов, например, таких как блоковый (blocking), кольцевой (ringing), москитный шум (mosquito), и мерцающий (flickering) артефактов, особенно при низком битрейте при кодировании. Сжатие блоков изображения по отдельности друг от друга нарушает корреляцию между пикселями на границах между блоками и приводит к появлению блоковых артефактов. Кольцевые артефакты возникают из-за потери высокочастотных коэффициентов ДКП при квантовании с большим (грубым) шагом квантования. Кольцевые артефакты схожи с феноменом Гиббса [1] и наиболее распространены вдоль сильно выделяющихся контуров. Москитный шум, в свою очередь, возникает от кольцевых артефактов во многих по отдельности сжатых фреймах при отображении в виде видео последовательности. Для intercode-фреймов москитный шум становиться более заметным в блоках на границах движущихся объектов и фона, которые содержат серьезные неточности межфреймового предсказания (interframe prediction) в оставшихся после сжатия сигналах [2]. Мерцающие артефакты [3], [4] появляются из-за различий в качестве среди фреймов в той же пространственной позиции. Это непостоянство возникает из-за временного искажения среди сжатых фреймов вызванного квантованием оставшегося сигнала. Мерцающие артефакты наиболее заметны в ровных областях, также появляются из-за различных уровней квантования для оптимизации искажения битрейта (метод rate-distortion optimization, RDO, RD).
Существующие методы по подавлению артефактов
Многие методы подавления шумов, основывающиеся на использовании фильтров, предлагались для уменьшения вышеперечисленных артефактов. Большинство из них основываются на усилении фреймов (frame-based enhancement). Для понижения блокового артефакта линейный фильтр нижних частот был применен в [5] с целью удаления высоких частот вызванных краями блоков на границах, но при этом была получена чрезмерная размытость, так как высокочастотные компоненты собственно изображения также были удалены. В [6]-[8], фильтры нижних частот были применены к коэффициентам ДКП сдвинутых блоков. В частности, адаптивные линейные фильтры были предложены в [7] и [8] для преодоления проблемы чрезмерного размытия изображений, но эти методы требуют довольно сложных вычислений. В [9] был предложен метод, основанный на проекциях на выпуклое множество с использованием мультифреймовых ограниченных множеств для уменьшения блоковых артефактов. Этот метод требует извлечения движений между фреймами и информации о квантовании из видео потока.
Для снижения кольцевых артефактов методы в [10] и [11] использовали линейные или нелинейные изотропные фильтры на областях где присутствовал кольцевой артефакт. Как подход, основанный на сжатии (encoder-based), [12] предлагает алгоритм формовки шума для нахождения оптимальных коэффициентов ДКП, которые приспосабливаются к дисперсиям шумов в различных областях. Все эти методы могут уменьшать круговые артефакты в каждом отдельном фрейме. Для работы с временными (temporal) характеристиками москитного шума, в[13] был применен пространственно-временной медианный фильтр для трансформации области в блоки 8 на 8. Улучшения в этом случае ограничились низкой корреляцией между коэффициентами ДКП пространственных блоков 8 на 8, а так же низкой компенсацией движений в последовательности
Большинством существующих методов мерцающие артефакты устраняются при внутрифреймовом кодировании (intraframe coding). В [3] считается, что при обеспечении оптимального уровня погрешности квантования в режиме внутрикадрового кодирования возможно понижение мерцающих артефактов. При внутрифреймовом кодировании [4] включает определение мерцающего артефакта в функции оптимизации как часть поиска оптимального предсказания и определения размера блока. Похожая идея реализуется в [14] для понижения мерцания в Motion JPEG 2000. Все эти подходы основаны на сжатии (coder-based).
Для более эффективного понижения временных артефактов, таких как москитный шум и мерцание следует применять не только пространственную, но и временную корреляцию пикселей.[20]

а) б)Рис. 1 – Пример блочного артефакта: а) исходное изображение, б) сжатое изображение
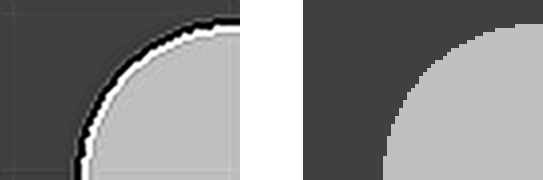
а) б)Рис. 2 – Пример кольцевого артефакта: а) сжатое изображение, б) изображение без кольцевого артефакта
 Рис. 3 – Пример москитного шума
Рис. 3 – Пример москитного шума
Fuzzy-фильтр
Fuzzy-фильтры, например описанные в [11] и [18], являются улучшениями медианных фильтров [19]. Предположим, что фильтр h применен по отношению к набору из Ω соседних пикселей x[m+m',n+n'] вокруг центрального пикселя x[m,n] для получения результата:
 ,
,
eго несмещенная форма с нормализацией:
 [20].
[20].
В (1) h(x[m+m',n+n'],x[m,n]) управляет влиянием входных данных x[m+m',n+n'],x[m,n] на результат. Для линейных фильтров, h не изменяется и не зависит от исходных данных. В случае нелинейного фильтра, h – это функция от входных данных, например для медианного фильтра
 ,
где round(u) ближайшее целое к u.[20]
,
где round(u) ближайшее целое к u.[20]
 Рис. 4 - Применение фильтра к пикселям изображениия (Анимация состоит из 21 кадра, размер файла - 137 Кб с задержкой в 0.75 мс между кадрами; количество циклов воспроизведения – 5)
Рис. 4 - Применение фильтра к пикселям изображениия (Анимация состоит из 21 кадра, размер файла - 137 Кб с задержкой в 0.75 мс между кадрами; количество циклов воспроизведения – 5)
Из-за независимости входных данных от коэффициентов фильтра, фильтр нижних частот, разработанный для эффективного использования на ровных областях, может вызывать размытие изображения. При подавлении артефактов, особенно в случае сжатия c низким битрейтом, желательно сохранить детали изображения помимо удаления артефактов. Этого можно добиться наложением ограничения, например такого, что если x[m+m',n+n'] находится далеко от x[m,n], то его влияние на результат мало. В таком случае коэффициенты фильтра h[k,l] должны удовлетворять условиям:
 [20]
[20]
 ,
где для вещественных чисел a > 0; b, c > 0; e ≅ 2.718281828. График (рис.5) функции Гаусса является характерной симметричной кривой, быстро спадающей на бесконечности. Параметр а задает высоту пика кривой, b позицию центра, а с – ширину кривой.
,
где для вещественных чисел a > 0; b, c > 0; e ≅ 2.718281828. График (рис.5) функции Гаусса является характерной симметричной кривой, быстро спадающей на бесконечности. Параметр а задает высоту пика кривой, b позицию центра, а с – ширину кривой.
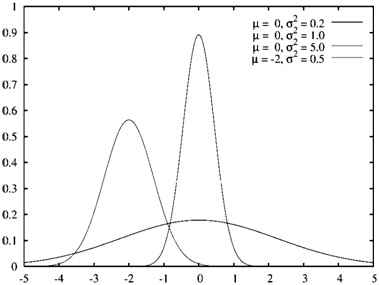 Рис. 5 – Нормированная Гауссова кривая с математическим ожиданием μ и дисперсией σ. Параметры функции: а = 1/(σ√(2π)); b = μ;c = σ.
Рис. 5 – Нормированная Гауссова кривая с математическим ожиданием μ и дисперсией σ. Параметры функции: а = 1/(σ√(2π)); b = μ;c = σ.
В нашем случае применим функцию Гаусса следующим образом:

где σ - параметр распространения входных данных, определяющий силу fuzzy-фильтра.[20] При этом влияние входного x[m,n] на результат всегда выше по сравнению с влиянием других пикселей:

Для тех же |x[m+m’,n+n’] – x[m,n]| , чем выше значение σ, тем большее влияние на результат имеет x[m+m’,n+n’] по сравнению с x[m,n]. Это означает, что x[m,n] будет более усреднен к x[m+m’,n+n’]. Меньшие значения σ оставляют сигнал x[m,n] более изолированным от соседних пикселей. Параметр распространения должен быть адаптивным к разным областям, например, более плавным или более детализированным.[20] Для сигналов нескольких размерностей fuzzy-фильтр в общем случае назначает фиксированное значение параметра распространения для каждого пикселя окрестности и игнорирует расстояние между ними. При сжатии изображений и видео, такие артефакты как блоковый, кольцевой или мерцающий направленные, и поэтому fuzzy-фильтр должен учитывать направления между x[n] и окружающими его пикселями x[m+m',n+n']. Этого можно добиться использованием адаптивного параметра распространения:

где σm – зависящая от позиции амплитуда параметра распространения σ, а K – это масштабирующая функция, которая зависит от направления между x[m+m',n+n'] и x[m,n].[20]
Направленный параметр распространения
При сильном сжатии, кольцевые артефакты в JPEG изображениях преобладают вдоль контуров и сила фильтра должна приспосабливаться к направлению контура. Например, на рис.6б фильтр должен применить более сильное сглаживание в горизонтальном направлении, а более слабое фильтрование - в вертикальном направлении, которое является направлением контуров в изображении.[20] Одной из основных косинусных форм параметра распространения, которая удовлетворяет этому требованию, является:

где Θ - угол между интересующим нас пикселем I[m,n] и окружающими пикселями I[m+m',n+n'] см рис.6а. σm - амплитуда параметра распространения, α и β – положительные факторы масштабирования, которые управляют максимумом и минимумом силы направленного фильтра.[20]

а) б)Рис. 6 – Пример направленных JPEG артефактов. а) исходное изображение. б) сжатое [20]
В (9), σ(Θ) принимает минимальное значение σ(Θ)=ασm при вертикальном направлении и максимальное σ(Θ)=(α+β)&sigma_m при горизонтальном направлении. Пример направленного параметра распространения показан на графике, на рис.7б со значениями параметров σ=15,α=0.5, β =3.5.
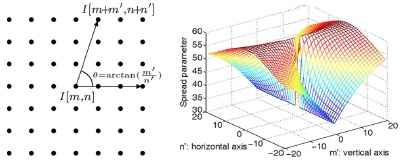
а) б)Рис. 7 – Угол и параметр распространения для направленного fuzzy-фильтра. а) угол Θ . б) параметр распространения [20]
Направленный fuzzy-фильтр, основанный на контурах изображения
Для настоящих изображений с более сложными контурами, наиболее сильная фильтрация применяется по направлению перпендикулярному к контуру. Используя оператор Собеля с приближенными производными по горизонтали и по вертикали градиента

можно определить контуры через величину градиента G=√(Gy²+Gx² ). Соответствующее направление градиента определяется как &Theta0=atan√(Gy/Gx).Функция распространения в этом случае определяется углом (Θ-Θ_0) вместо Θ в (9), где углы Θ и Θ0 определены как показано на рис.8.[20] Для применения к разным областям изображения, используется среднеквадратичное отклонение STD(I[m,n]) пикселей в окне W с центром в I[m,n] для контроля амплитуды параметра распространения σm в (9) следующим образом:

где STDmax и STDmin соответственно максимальное и минимальное значения всех значений STD(I[m,n]) в текущем фрейме, σm – максимальное значение параметра распространения и γ - фактор масштабирования в пределах [0,1]. σm масштабируется к γσ0 σ0 поэтому fuzzy-фильтр применяется с σm=γσ0 для областей с наименьшей активностью.[20] Регулируя sigma;0 и γ, достигается необходимый баланс между сохранением контуров и подавлением артефактов.
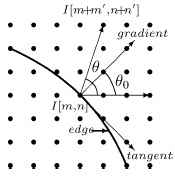 Рис. 8 – Углы Θ и Θ0 для направленного fuzzy-фильтра, основанного на контурах изображения [20]
Рис. 8 – Углы Θ и Θ0 для направленного fuzzy-фильтра, основанного на контурах изображения [20]
Предлагаемый алгоритм для направленной fuzzy-фильтрации, основанной на контурах изображения, показан на рис.9. Вначале выделяются пиксели контура путем сравнения значения градиента с опытно определенным порогом. Пиксели контура не фильтруются, т.к. они не являются пикселями кольцевого артефакта. Для пикселей не контура, в том случае если пиксели контура отсутствуют в том же блоке изображения, кольцевые артефакты считаются не связанными с каким-либо направлением и отфильтровываются обычными изотропным fuzzy-фильтром. Для других пикселей не контуров для контроля направленного параметра распространения используется угол между контуром и ближайшим пикселем контура.
 Рис. 9 – Алгоритм работы направленного fuzzy-фильтра [20]
Рис. 9 – Алгоритм работы направленного fuzzy-фильтра [20]
Заключение
В качестве вывода можно заметить, что существует большое количество методов борьбы с артифактами в изображениях и видео последовательностях. Были рассмотрены наиболее часто встречающиеся в сжатых изображениях и видео последовательностях артефакты, а именно блоковый, кольцевой, москитный шум, и мерцающий, и источники их появления. Проанализированы некоторые существующие методы для подавления артефактов.
В результате, основываясь на изученных теоретических матерталах, в пакете MATLAB была разработана модель направленного адаптивного fuzzy-фильтра для обработки полутоновых изображений. Выполненные исследования подтвердили эффективность разработанной по рассмотренным алгоритмам модели фильтра при подавлении умеренных артефактов.
На данный момент работа не закончена. Дальнейшие работы над рассмотренным фильтром могут быть связаны с попытками усовершенствования его работы, в частности по улучшению силы фильтра, либо по сохранению контуров самого изображения. Возможно будут предприняты попытки применения рассмотренных алгоритмов фильтрации для нестандартых видов представления изображений, например в гексагональной решетке (в отличие от традиционной пямоугольной). Так же дальнейшие работы могут быть направлены на применение фильтра для обработки полноцветных изображений и видеозаписей.
Cписок литературы
- Jerri A., The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations. Dordrecht, The Netherlands: Kluwer, 1998.
- Kaneko M., Hatori Y, Koike A., “Improvements of transform coding algorithm for motion-compensated interframe prediction errors-DCT/SQ coding,” IEEE J. Sel Areas Commun., vol. 5, no. 8, pp. 1068–1078, Aug. 1987.
- Fan X., Gao W., Lu Y., Zhao D., “Flicking reduction in all intra frame coding,” Joint Video Team of ISO/IEC MPEG and ITU-T VCEG, JVT-E070, Oct. 2002.
- Sakaida S., Iguchi K., Gohshi S., Fujita Y., “Adaptive quantization control for reducing flicker of AVC/H.264 intra frames,” presented at the Picture Coding Symp., Dec. 2004.
- Jarske T., Haavisto P., Defee I., “Post-filtering methods for reducing blocking effects from coded images,” IEEE Trans. Cosum. Electron., vol. 40, no. 8, pp. 521–526, Aug. 1994.
- Nosratinia A., “Embedded post-processing for enhancement of compressed images,” in Proc. IEEE Data Compression Conf., 1999, pp. 62–71.
- Chen T., Wu H., Qiu B., “Adaptive postfiltering of transform coefficients for the reduction of blocking artifacts,” IEEE Trans. Circuits Syst. Video Technol., vol. 11, no. 5, pp. 594–602, May 2001.
- Liu S., Bovik A., “Efficient DCT-domain blind measurement and reduction of blocking artifacts,” IEEE Trans. Circuits Syst. Video Technol., vol. 12, no. 12, pp. 1139–1149, Dec. 2002.
- Gunturk B., Altunbasak Y., Mersereau R. M., “Multiframe blocking-artifact reduction for transform-coded video,” IEEE Trans. Circuits Syst. Video Technol., vol. 12, no. 4, pp. 276–282, Apr. 2002.
- Oguz S., Hu Y., Nguyen T., “Image coding ringing artifact reduction using morphological post-filtering,” in Proc. IEEE Int. Work. Multimedia Signal Processing, 1998, pp. 628–633.
- Kong H., Nie Y., Vetro A., Sun H., Barner K., “Adaptive Fuzzy Post-Filtering for Highly Compressed Video,” in Prof. IEEE Int. Conf. Image Proc., 2004, pp. 1802–1806.
- Westen S., Lagendijk R., Biemond J., “Adaptive spatial noise shaping for DCT based image compression,” in Proc. IEEE Int. Conf. Acoustics, Speech and Signal Processing, May 1996, vol. 4, pp. 2124–2127.
- DelCorso S., Miro C., Jung J., “MNR: A novel approach to correct MPEG temporal distortions,” IEEE Trans. Consum. Electron., vol. 49, no. 2, pp. 229–236, Feb. 2003.
- Leontaris A., Tonomura Y., Nakachi T., Cosman P., “Flicker suppression in JPEG2000 using segmentation-based adjustment of block truncation lengths,” in Proc. IEEE Int. Conf. Acoustics, Speech and Signal Processing, Apr. 2007, vol. 1, pp. 1117–1120.
- Smith S. M., Brady J.M., “Susan-a newapproach to lowlevel image processing,” Int. J. Comput. Vis., vol. 23, pp. 45–78, 1997.
- Tomasi C., Manduchi R., “Bilateral filtering for gray and color images,” in Proc. Int. Conf. Comput. Vis., 1998, p. 839846.
- Gelasca E. D., Ebrahimi T., “On evaluating metrics for video segmentation algorithms,” presented at the 2nd Int. Workshop on Video Processing and Quality Metrics for Consumer Applications, Jan. 2006.
- Nie Y., Barner K., “The fuzzy transformation and its application in image processing,” IEEE Trans. Image Process., vol. 15, no. 4, pp. 910–927, Apr. 2006.
- Justusson B., “Median filtering: Statistical properties,” in Two Dimensional Digital Signal Processing II, T. S. Huang, Ed. Berlin, Germany: Springer-Verlag, 1981.
- Vo D., Nguyen T., Yea S., Vetro A., "Adaptive Fuzzy Filtering for Artifact Reduction in Compressed Images and Videos", IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 18, NO. 6, JUNE 2009