
Гридiн Дмитро Олександрович
Тема випускної роботи:
Fuzzy-фільтрація для усунення артефактів у регіонах інтересу у відеопослідовностях
Науковий керівник: Самощенко О.В.
Реферат з теми «Fuzzy-фiльтрацiя для усyнення артефактiв y регiонах iнтересу у вiдеопослiдовностях»
Содержание
Вступ
Актуальнiсть теми
Наукова значимість роботи
Практична цінність результатів роботи
Об'єкт і предмет досліджень
Огляд досліджень за темою
Основнi рiзновиди артефактiв
Iснуючi методи подавлення артефактiв
Fuzzy-фiльтр
Спрямований параметр поширення
Спрямований fuzzy-фільтр, заснований на контурах зображення
Висновок
Перелiк лiтератури
Вступ
У цифровій обробці сигналів довгий час досліджувалися і розроблялися методи для перетворення звукових або відео сигналів в цифрову форму. При будь-якому перетворенні можливі втрати, але в той же час користувачі мають можливості для додаткових перетвореннь даних для зменшення їх розміру, наприклад для економії простору на носії інформації, або для заощадження часу при передачі даних, наприклад через Internet. Природно, що подібні перетворення не можуть виконуватися без втрат або спотворення даних. У зображеннях і відео ці спотворення найчастіше виражаються у вигляді появи небажаних перешкод - артефактів.
Актуальнiсть теми
Пригнічення артефактів для поліпшення якості зображення є дуже актуальним завданням, оскільки відновлення пошкоджених чи зашумленных зображень або відеозаписів в різних ситуаціях може бути корисною і цінною операцією.
Наукова значимість роботи
Наукова значимість цієї роботи полягає в розробці поліпшеного методу усунення артефактів в регіонах інтересу відеопослідовностей.
Практична цінність результатів роботи
В ході виконання роботи після проведення моделювання з поліпшеним методом усунення артефактів передбачається отримати якісніше зображення або відеопослідовність після обробки початкового спотвореного зображення або відео.
Об'єкт і предмет досліджень
Об'єктом досліджень є зображення, кадр відеопослідовності, що містить різні характерні фрагменти. Предметом досліджень є методи методи фільтрації і обробки зображень.
Огляд досліджень за темою
Серед робіт магистрантiв і співробітників ДонНТУ тематика відновлення зображень не дуже поширена. Проте є велика кiлькiсть цікавих робіт з обробки зображень різними методами, результати яких можуть бути використані при розгляді досліджуваної теми. З Деякими з найцікавіших робіт можна ознайомитися в розділі «Посилання».
В цілому є велика кiлькiсть робіт з відновлення зображень і відеопослідовностей, у тому числі і досліджуваним методом fuzzy- фільтрації. Часто розроблені алгоритми мають деякі схожі риси в методиці виконання фільтрації. Також варто відмітити, що більшість існуючих робіт в цьому напрямі представлена іноземними дослідниками.
Основнi результати
Основнi рiзновиди артефактiв
Сигнали, що були стиснутi за допомогою блокових алгоритмів, часто страждають від різних артефактів, наприклад, таких як блоковий (blocking), кільцевий (ringing), москітний шум(mosquito), і мерехтливий (flickering) артефакти, особливо при низькому бітрейті при кодуванні. Стискування блоків зображення окремо один від одного порушує кореляцію між пікселями на межах між блоками і призводить до появи блокових артефактів. Кільцеві артефакти виникають через втрату високочастотних коефіцієнтів ДКП при квантуванні з великим (грубим) кроком квантування. Кільцеві артефакти схожі з феноменом Гіббса [1] і найбільш поширені уздовж контурів, що сильно виділяються. Москітний шум, у свою чергу, виникає від кільцевих артефактів у багатьох окремо стислих фреймах при відображенні у вигляді відео послідовності. Для intercode-фреймів москітний шум стає помітнішим у блоках на межах об'єктів, що рухаються, і фону, які містять серйозні неточності міжфреймового передбачення (interframe prediction) в сигналах, що залишилися після стискування [2]. Мерехтливі артефакти [3], [4] з'являються через відмінностi в якості серед фреймів в тій же просторовій позиції. Ця непостійність виникає через часове спотворення серед стиснутих фреймів, що викликано квантуванням сигналу, що залишився. Мерехтливі артефакти найбільш помітні в рівних областях, також з'являються із-за різних рівнів квантування для оптимізації спотворення бітрейта(метод rate - distortion optimization, RDO, RD).
Iснуючi методи подавлення артефактiв
Багато методів подавлення шумів, що грунтуються на використанні фільтрів, пропонувалися для зменшення вищеперелічених артефактів. Більшість з них грунтуються на пiдиленні фреймів(frame - based enhancement). Для пониження блокового артефакту лінійний фільтр нижніх частот був застосований в [5] з метою видалення високих частот викликаних краями блоків на межах, але при цьому була отримана надмірна розмитість, оскільки високочастотні компоненти власне зображення також були видалені. У [6]-[8], фільтри нижніх частот були застосовані до коефіцієнтів ДКП зрушених блоків. Зокрема, адаптивні лінійні фільтри були запропоновані в [7] і [8] для подолання проблеми надмірного розмиття зображень, але ці методи вимагають досить складних обчислень. У [9] був запропонований метод, заснований на проекціях на опуклу множину з використанням мультифреймових обмежених множин для зменшення блокових артефактів. Цей метод вимагає витягання рухів між фреймами і інформації про квантування з відео потоку.
Для зниження кільцевих артефактів методи в [10] і [11] використали лінійні або нелінійні ізотропні фільтри до областей де був присутнім кільцевий артефакт. Як підхід, заснований на стискуванні(encoder - based), [12] пропонує алгоритм формування шуму для знаходження оптимальних коефіцієнтів ДКП, які пристосовуються до дисперсій шумів в різних областях. Усі ці методи можуть зменшувати кругові артефакти в кожному окремому фреймі. Для роботи з часовими(temporal) характеристиками москітного шуму, в[13] був застосований просторово-часовий медіанний фільтр для трансформації області у блоки 8 на 8. Поліпшення в цьому випадку обмежилися низькою кореляцією між коефіцієнтами ДКП просторових блоків 8 на 8, а так само низькою компенсацією рухів в послідовності.
Більшістю існуючих методів мерехтливі артефакти усуваються при внутрішньофреймовому кодуванні(intraframe coding). У [3] вважається, що при забезпеченні оптимального рівня погрішності квантування в режимі внутрішньокадрового кодування можливе пониження мерехтливих артефактів. При внутрішньофреймовому кодуванні [4] включає визначення мерехтливого артефакту у функції оптимізації як частину пошуку оптимального пророцтва і визначення розміру блоку. Схожа ідея реалізується в [14] для зниження мерехтіння в Motion JPEG 2000. Усі ці підходи засновані на стисканнi (coder-based).
Для ефективнішого пониження тимчасових артефактів, таких як москітний шум і мерехтіння слід застосовувати не лише просторову, але і часову кореляцію пікселів.[20]

а) б)Рис. 1 - Приклад блокового артефакту: а) початкове зображення, б) стиснуте зображення
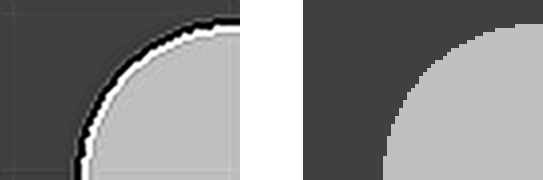
а) б)Рис. 2 – Приклад кільцевого артефакту: а) стиснуте зображення, б) зображення без кільцевого артефакту
 Рис. 3 – Приклад москітного шуму
Рис. 3 – Приклад москітного шуму
Fuzzy-фiльтр
Fuzzy- фільтри, наприклад описані в [11] і [18], є поліпшеннями медіанних фільтрів [19]. Припустимо, що фільтр h застосований по відношенню до набору з Ω сусідніх пікселів x[m+m ', n+n'] навколо центрального пікселя x[m, n] для отримання результату :

Його незміщена форма з нормалізацією:
 [20]
[20]
У(1) h(x[m+m ', n+n'],x[m, n]) керує впливом вхідних даних x[m+m ', n+n'],x[m, n] на результат. Для лінійних фільтрів, h не змінюється і не залежить від початкових даних. У разі нелінійного фільтру, h - це функція від вхідних даних, наприклад для медіанного фільтру
 ,
Де round(u) найближче цiле до u.[20]
,
Де round(u) найближче цiле до u.[20]
 Рис. 4 - Застосування фільтру до пікселів изображениия (Анімація складається з 21 кадру, розмiр - 137 Кб із затримкою в 0.75 мс між кадрами; кількість циклів відтворення - 5)
Рис. 4 - Застосування фільтру до пікселів изображениия (Анімація складається з 21 кадру, розмiр - 137 Кб із затримкою в 0.75 мс між кадрами; кількість циклів відтворення - 5)
Через незалежнiсть вхідних даних від коефіцієнтів фільтру, фільтр нижніх частот, розроблений для ефективного використання на рівних областях, може викликати розмиття зображення. При подавленi артефактів, особливо у разі стискання з низьким бітрейтом, бажано зберегти деталі зображення окрім видалення артефактів. Цього можна добитися накладенням обмеження, наприклад такого, що якщо x[m+m ', n+n'] знаходиться далеко від x[m, n], те його вплив на результат невелике. У такому разі коефіцієнти фільтру h[k, l] повинні задовольняти умовам:
 [20]
[20]
 ,
де для дійсних чисел a > 0; b, c > 0; e ≅ 2.718281828. Графік (рис.5) функції Гауса є характерною симетричною кривою, що швидко спадає на нескінченності. Параметр а задає висоту піку кривої, b позицію центру, а з - ширину кривої.
,
де для дійсних чисел a > 0; b, c > 0; e ≅ 2.718281828. Графік (рис.5) функції Гауса є характерною симетричною кривою, що швидко спадає на нескінченності. Параметр а задає висоту піку кривої, b позицію центру, а з - ширину кривої.
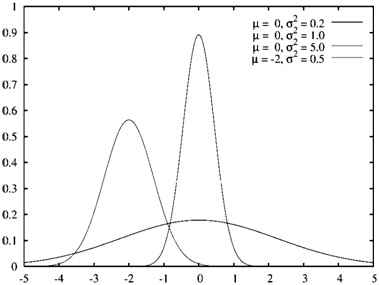 Рис. 5 – Нормована крива Гауса з математичним очікуванням μ і дисперсією σ. Параметри функцiї: а = 1/(σ√(2π)); b = μ;c = σ.
Рис. 5 – Нормована крива Гауса з математичним очікуванням μ і дисперсією σ. Параметри функцiї: а = 1/(σ√(2π)); b = μ;c = σ.
B нашому випадку застосуємо функцію Гауса таким чином:

де σ - параметр поширення вхідних даних, що визначає силу fuzzy-фільтру.[20] При цьому вплив вхідного x[m, n] на результат завжди вище в порівнянні з впливом інших пікселів:

Для тих же |x[m+m ', n+n'] - x[m, n]|, чим вище значення σ, тим більший вплив на результат має x[m+m ', n+n'] в порівнянні з x[m, n]. Це означає, що x[m, n] буде більше усереднений до x[m+m ', n+n'] . Менші значення σ залишають сигнал x[m, n] більше ізольованим від сусідніх пікселів. Параметр поширення має бути адаптивним до різних областей, наприклад, плавніших або більше деталізованих.[20] Для сигналів декількох розмірності fuzzy-фільтр в загальному випадку призначає фіксоване значення параметра поширення для кожного пікселя околиці і игнорує вiдстань мiж ними. При стискуванні зображень і відео, такі артефакти як блоковий, кільцевий або мерехтливий спрямовані, і тому fuzzy- фільтр повинен враховувати напрями між x[n] і пікселями x, що оточують його[m+m ', n+n']. Цього можна добитися використанням адаптивного параметра поширення:

де σm – залежна від позиції амплітуда параметра поширення σ, а K – це масштабуюча функція, яка залежить від напрями між x[m+m',n+n'] и x[m,n].[20]
Спрямований параметр поширення
При сильному стискуванні, кільцеві артефакти в JPEG зображеннях переважають уздовж контурів і сила фільтру повинна пристосовуватися до напряму контура. Наприклад, на рис.6б фільтр повинен застосувати сильніше згладжування в горизонтальному напрямі, а слабкіше фільтрування - у вертикальному напрямі, який є напрямом контурів в зображенні.[20] Однією з основних косинусних форм параметра поширення, яка задовольняє цій вимозі, є:

де Θ - кут між пікселем I, що цікавить нас[m, n] і навколишніми пікселями I[m+m ', n+n'] див. рис.6а. σm - амплітуда параметра поширення, α та β – позитивні чинники масштабування, які управляють максимумом і мінімумом сили спрямованого фільтру.[20]

а) б)Рис. 6 – Приклад спрямованих JPEG артефактів. а) початкове зображення. б) стиснуте [20]
В (9), σ(Θ) набуває мінімального значення σ(Θ)=ασm при вертикальному напрямі і максимальне σ(Θ)=(α+β)&sigma_m при горизонтальному напрямі. Приклад спрямованого параметра поширення показаний на графіці, на рис.7б зі значеннями параметрів σ=15,α=0.5, β =3.5.
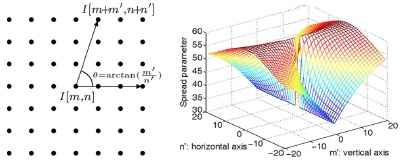
а) б)Рис. 7 – Кут і параметр поширення для спрямованого fuzzy-фільтру. а) кут Θ . б) параметр поширення [20]
Спрямований fuzzy-фільтр, заснований на контурах зображення
Для реальних зображень зi складнішими контурами, найбільш сильна фільтрація застосовується по напряму перпендикулярному до контура. Використовуючи оператор Собеля з наближеними похідними по горизонталі і по вертикалі градієнта

можна визначити контури через величину градієнта G=√(Gy²+Gx² ). Відповідний напрям градієнта визначається як &Theta0=atan√(Gy/Gx).Функція поширення в цьому випадку визначається кутом (Θ-Θ_0) замiсть Θ в (9), де кути Θ и Θ0 визначені як показано на рис.8.[20] Для застосування до різних областей зображення, використовується середньоквадратичне відхилення STD(I[m, n]) пікселів у вікні W з центром в I[m, n] для контролю амплітуди параметра поширення σm у (9) таким чином:

де STDmax і STDmin відповідно максимальне і мінімальне значення усіх значень STD(I[m, n]) в поточному фреймі σm – максимальне значення параметра поширення і γ - чинник масштабування в межах [0,1]. σm масштабується до γσ0 σ0 тому fuzzy- фільтр застосовується с σm=γσ0 для областей з найменшою активністю.[20] Регулюючи σ0 и γ, досягається необхідний баланс між збереженням контурів і подавленням артефактів.
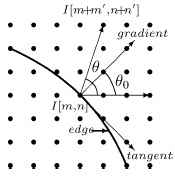 Рис. 8 – Кути Θ и Θ0 для спрямованого fuzzy- фільтру, заснованого на контурах зображення [20]
Рис. 8 – Кути Θ и Θ0 для спрямованого fuzzy- фільтру, заснованого на контурах зображення [20]
Запропонований алгоритм для спрямованої fuzzy-фільтрації, заснованої на контурах зображення, показаний на рис.9. Спочатку виділяються пікселі контура шляхом порівняння значення градієнта з досвідчено певним порогом. Пікселі контура не фільтруються, оскільки вони не є пікселями кільцевого артефакту. Для пікселів не контура, у тому разі якщо пікселі контура відсутні в тому ж блоці зображення, кільцеві артефакти вважаються не пов'язаними з яким-небудь напрямом і фільтруються звичайними ізотропним fuzzy- фільтром.фільтром.фільтром. Для інших пікселів не контурів для контролю спрямованого параметра поширення використовується кут між контуром і найближчим пікселем контура.
 Рис. 9 – Алгоритм роботи спрямованого fuzzy-фільтру [20]
Рис. 9 – Алгоритм роботи спрямованого fuzzy-фільтру [20]
Висновок
В якості виведення можна помітити, що існує велика кількість методів боротьби з артифактами в зображеннях і відео послідовностях. Були розглянуті що найчастіше зустрічаються в стислих зображеннях і відео послідовностях артефакти, а саме блоковий, кільцевий, москітний шум, і мерехтливий, і джерела їх появи. Проаналізовані деякі існуючі методи для пригнічення артефактів.
В результаті, взявши за основу розглянутi теоретичнi матерiали, в пакеті MATLAB була розроблена модель спрямованого адаптивного fuzzy- фільтру для обробки півтонових зображень. Виконані дослідження пiдтведили ефективність розробленої моделі фільтру для пригнічення помірних артефактів.
В поточний момент робота не завершена. Подальші роботи над розглянутим фільтром можуть бути пов'язані із спробами удосконалення його роботи, зокрема по поліпшенню сили фільтру, або по збереженню контурів самого зображення. Можливо, будутб виконанi спроби застосування розглянених алгоритмiв фiльтрацiї для нестандартних видiв представлення зображеннь, наприклад в гексагональнiй решiтцi (на вiдмiну вiд традицiйної прямокутної). Так само подальші роботи можуть бути спрямовані на застосування фільтру для обробки повнокольорових зображень і відеозаписів.
Перелiк лiтератури
- Jerri A., The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations. Dordrecht, The Netherlands: Kluwer, 1998.
- Kaneko M., Hatori Y, Koike A., “Improvements of transform coding algorithm for motion-compensated interframe prediction errors-DCT/SQ coding,” IEEE J. Sel Areas Commun., vol. 5, no. 8, pp. 1068–1078, Aug. 1987.
- Fan X., Gao W., Lu Y., Zhao D., “Flicking reduction in all intra frame coding,” Joint Video Team of ISO/IEC MPEG and ITU-T VCEG, JVT-E070, Oct. 2002.
- Sakaida S., Iguchi K., Gohshi S., Fujita Y., “Adaptive quantization control for reducing flicker of AVC/H.264 intra frames,” presented at the Picture Coding Symp., Dec. 2004.
- Jarske T., Haavisto P., Defee I., “Post-filtering methods for reducing blocking effects from coded images,” IEEE Trans. Cosum. Electron., vol. 40, no. 8, pp. 521–526, Aug. 1994.
- Nosratinia A., “Embedded post-processing for enhancement of compressed images,” in Proc. IEEE Data Compression Conf., 1999, pp. 62–71.
- Chen T., Wu H., Qiu B., “Adaptive postfiltering of transform coefficients for the reduction of blocking artifacts,” IEEE Trans. Circuits Syst. Video Technol., vol. 11, no. 5, pp. 594–602, May 2001.
- Liu S., Bovik A., “Efficient DCT-domain blind measurement and reduction of blocking artifacts,” IEEE Trans. Circuits Syst. Video Technol., vol. 12, no. 12, pp. 1139–1149, Dec. 2002.
- Gunturk B., Altunbasak Y., Mersereau R. M., “Multiframe blocking-artifact reduction for transform-coded video,” IEEE Trans. Circuits Syst. Video Technol., vol. 12, no. 4, pp. 276–282, Apr. 2002.
- Oguz S., Hu Y., Nguyen T., “Image coding ringing artifact reduction using morphological post-filtering,” in Proc. IEEE Int. Work. Multimedia Signal Processing, 1998, pp. 628–633.
- Kong H., Nie Y., Vetro A., Sun H., Barner K., “Adaptive Fuzzy Post-Filtering for Highly Compressed Video,” in Prof. IEEE Int. Conf. Image Proc., 2004, pp. 1802–1806.
- Westen S., Lagendijk R., Biemond J., “Adaptive spatial noise shaping for DCT based image compression,” in Proc. IEEE Int. Conf. Acoustics, Speech and Signal Processing, May 1996, vol. 4, pp. 2124–2127.
- DelCorso S., Miro C., Jung J., “MNR: A novel approach to correct MPEG temporal distortions,” IEEE Trans. Consum. Electron., vol. 49, no. 2, pp. 229–236, Feb. 2003.
- Leontaris A., Tonomura Y., Nakachi T., Cosman P., “Flicker suppression in JPEG2000 using segmentation-based adjustment of block truncation lengths,” in Proc. IEEE Int. Conf. Acoustics, Speech and Signal Processing, Apr. 2007, vol. 1, pp. 1117–1120.
- Smith S. M., Brady J.M., “Susan-a newapproach to lowlevel image processing,” Int. J. Comput. Vis., vol. 23, pp. 45–78, 1997.
- Tomasi C., Manduchi R., “Bilateral filtering for gray and color images,” in Proc. Int. Conf. Comput. Vis., 1998, p. 839846.
- Gelasca E. D., Ebrahimi T., “On evaluating metrics for video segmentation algorithms,” presented at the 2nd Int. Workshop on Video Processing and Quality Metrics for Consumer Applications, Jan. 2006.
- Nie Y., Barner K., “The fuzzy transformation and its application in image processing,” IEEE Trans. Image Process., vol. 15, no. 4, pp. 910–927, Apr. 2006.
- Justusson B., “Median filtering: Statistical properties,” in Two Dimensional Digital Signal Processing II, T. S. Huang, Ed. Berlin, Germany: Springer-Verlag, 1981.
- Vo D., Nguyen T., Yea S., Vetro A., "Adaptive Fuzzy Filtering for Artifact Reduction in Compressed Images and Videos", IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 18, NO. 6, JUNE 2009