
Gridin Dmitriy
Subject of master's work
Fuzzy-filtering for artifact reduction in the regions of interest in video sequences
Scientific adviser: Samoshchenko Alexander
Abstract
Contents
Introduction
Relevance of the master's work topic
The scientific innovation of the work
Expected practical results
Object and subject of research
Main types of artifacts
Existing artifact removal methods
Fuzzy filter
Directional Spread Parameter
Edge-Based Directional Fuzzy Filter
Conclusions
References
Introduction
Methîds of sound and video signal ñonversion had been studied and developed in digital signàl processing for a long time. Every conversion has possibility of data loss, but in the same time users have opportunities for additional operations in order to reduce size of data, for example to save some space on data carrier or to transmit data through Internet. Naturally, these transformations can not be achieved without losing and distortion of data. Most of the times in images or video this appears in the form of artifacts.
Relevance of the master's work topic
Artifact reduction in order to improve image quality is very important in the video data digital processing, because restoration of damaged or noisy images and videos could be really useful and vital operation in some circumstances.
The scientific innovation of the work
The scientific innovation of this work is to develop an improved artifact reduction method of video sequence frame.
Expected practical results
As a result of research it's expected to achieve images or videos with better quality after processing original distorted image or video.
Object and subject of research
The object of research is the image, frame sequences containing different fragments. The subject of research are methods of artifact reduction and image or video processing. Ïðåäìåòîì èññëåäîâàíèé ÿâëÿþòñÿ ìåòîäû ìåòîäû ôèëüòðàöèè è îáðàáîòêè èçîáðàæåíèé.
Main results
Main types of artifacts
Block-based compressed signals often suffer from different artifacts, such as blocking, ringing, mosquito, and flickering, especially at low-bit-rate coding. Separately compressing each block breaks correlation between the pixels at the borders of blocks and causing blocking artifacts. Ringing artifacts appear due to loss of high frequences DCT when quantizing with a coars quantization step. Ringing artifacts are similar to Gibbs phenomenon [1] and most prevalent along the strong edges. Mosqito noise appears from ringing artifacts in many separately compressed frames when they displayed as sequence. For intercoded frames mosqito artifact become more noticable in blocks on the bounds of moving objects and background, which contain significant interframe prediction errors in residual signals [2]. Filckering artifacts [3], [4] appear due to the inconsistency in quality of frames in the same spatial position. The inconsistency happens due temporal distortion in compressed frames caused by quantization of residual signal. Flickering artifacts, which are more noticable in flat regions, also appear due to different quantization levels for rate-distortion optimization.
Existing artifact removal methods
Many filter-based denoising methods were proposed to reduse these artifacts. Most of them are frame-based enhancement. Linear low-pass filter was used in [5] for blocking artifact reduction to remove high frequencies caused by block's edges on the borders, but excessive blur was gained since high frequencies components of the image were also removed. In [6]-[8], low-pass filters were applied to DCT coefficients of shifted blocks. In particular, adaptive linear filters were proposed in [7] and [8] to overcome over-blurring problems, but those methods require usage of difficult computations. In [9] áa projections onto convex set-based method was proposed along with using multiframe constraint sets to reduce the blocking artifacts. That method required the motion extraction between the frames and quantization information from video stream.
For ringing artifacts reduction methods from [10] and [11] used linear or non-linear isotropic filters for ringing areas. As encoder-based method, [12] propoces a noise shaping algorithm to find optimal DCT coefficients, which adapts to noise dispercions in different areas. All these methods can reduce ringing artifacts in each single frame. In order to work with temporal characteristics of mosquito noise, spatio-temporal median filter was applied in [13] to transform area into 8 x 8 blocks. The improvement in this case were limited by low correlation between DCT coefficients of the spatial 8 x 8 blocks and also low motion compensation in the scheme.
For flickering artifacts removal, most of existing methods use intraframe coding. In [3] the quantization error is considered to obtain the optimalintra prediction mode and to help reducing the flickering artifact. Also for intraframe coding [4] includes flickering artifact detection in optimisation function as part of search of optimal prediction and block size determination. Similar idea is implemented in [14] for flickering artifact reduction in Motion JPEG 2000. All these methods are coder-based.
For more effective temporal artifacts reduction, such as mosquito noise and flickering, not only spatial, but also temporal correlation should be used.[20]

à) b)Fig. 1 – Blocking artifact example: à) original image, b) compressed image
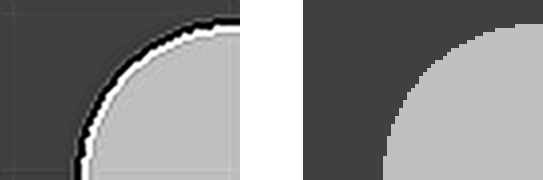
à) b)Fig. 2 – Ringing artifact example: à) compressed image, á)image without ringing artifact
 Fig. 3 – Mosquito noise example
Fig. 3 – Mosquito noise example
Fuzzy filter
Fuzzy filters, such as described in [11] and [18], are improvements of median filters [19]. Assume that filter h applied to a set of Ω neighboring pixels x[m+m',n+n'] around center x[m,n] in order to obtain result:

It's unbiased form with normalization:
 [20]
[20]
In (1) h(x[m+m',n+n'],x[m,n]) controls the contribution of the input x[m+m',n+n'],x[m,n] to the output. For linear filters, h is fixed and input-independent. In case of non-linear filter, h – is a function of the input, for example for median filter
 ,
where round(u) is the nearest integer to u.[20]
,
where round(u) is the nearest integer to u.[20]
 Fig. 4 - Applying the filter to pixels of picture (Animation consists of 21 frames, file size - 137 Kbytes with delay of 0.75 ms between the frames; number of cycles – 5)
Fig. 4 - Applying the filter to pixels of picture (Animation consists of 21 frames, file size - 137 Kbytes with delay of 0.75 ms between the frames; number of cycles – 5)
Due to the input independence of filter coefficients, low-pass filter, designed for effective usage for flat areas, can cause image blurring. In artifact reduction, especially for low bit-rate compression, it is necessary to save image details besides artifact removal. This can be achieved by imposing the constraint such that if x[m+m',n+n'] is far from x[m,n], òits contribution to the
output is small. In that case, the filter coefficients h[k,l] follow the constraints:

The membership function is proposed to be used as h(x[m+m',n+n' ],x[m,n] ). There are many functions which
fulfill these requirements. For example, one of them is Gaussian membership function. For this function
 ,[20]
,[20]
where a > 0; b, c > 0; e ≅ 2.718281828 for real numbers. Gaussian functuon's graph (fig.5) is symmetric curve, quickly fading into infinity. Parameter à sets height of curve's peak, b - center position, and ñ – weight of the curve.
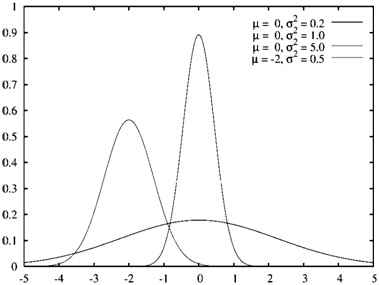 Fig. 5 – Normalized Gaussian curve with expected value μ and variance σ. The corresponding parameters are à = 1/(σ√(2π)); b = μ;c = σ.
Fig. 5 – Normalized Gaussian curve with expected value μ and variance σ. The corresponding parameters are à = 1/(σ√(2π)); b = μ;c = σ.
In out case Gaussian function is applied this way:

where σ - spread parameter of the input, which controls fuzzy filter strentgh.[20] Note that the contribution of the input to the output is always highest compared to the contribution of other pixels:

For the same |x[m+m’,n+n’] – x[m,n]| , the higher σ is, the higher the contribution of x[m+m’,n+n’] relatively compared to the contribution of x[m,n]. It means, that x[m,n] will be more averaged to x[m+m’,n+n’]. Lower values of σ will keep the signal x[m,n] more isolated from its neighboring pixels. Spread parameter should be adaptive to different areas, more soft or more detalized.[20] For multidimensional signals fuzzy filter assignes fixed value of spread parameter for each pixel of the neighborhood and ignores the relative position between them. In image and video compression, artifacts such as blocking, ringing or flickering artifacts are directional, so fuzzy filter should consider the directions between x[n] and surrounding pixels x[m+m',n+n']. This can be achieved by an adaptive spread parameter:

where σm – is a position-dependent amplitude of the spread parameter σ, ànd K – is the scaling function controlled by the direction of x[m+m',n+n'] and x[m,n].[20]
Directional Spread Parameter
When highly compressed, ringing artifacts in JPEG images images are prevalent along strong edges and the filter strength should adapt to the edge direction. For example, in fig.6b filter should apply stronger smoothing in horizontal direction, ànd weaker filtering in vertical direction, which is the edge direction of the image.[20] One of general cosine-based forms of spread parameter which satisfiesthis requirement is:

where Θ - is direction between pixel of interest I[m,n] and surrounding pixels I[m+m',n+n'] as shown on fig.7à. &sigma:m - amplitude of the spread parameter, α and β are positive scaling factors, which control the maximum and minimum strength of the directional filter.

à) b)Fig. 6 – Example of directional JPEG artifacts. à) original image. b) compressed image [20]
In (9), σ(Θ) attains the minimum value σ(Θ)=ασm in the vertical direction and the maximum value σ(Θ)=(α+β)&sigma_m in horizontal direction. An example of the directional spread parameter is plotted in fig.6b with σ=15,α=0.5, β =3.5.
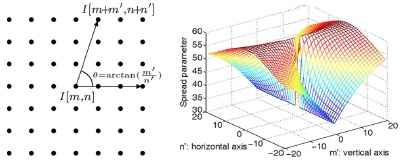
à) b)Fig 7 – Angle and spread parameter for directional fuzzy filter. à) angle Θ . b) spread parameter [20]
Edge-Based Directional Fuzzy Filter
For real images with more complicated edges, the strongest filtering is applied to direction perpendicular to the edge. Using Sobel operator with horizontal and vertical derivative approximation of the gradient

the edges are detected by using the gradient magnitude G=√(Gy²+Gx² ). Corresponding direction is determined by &Theta0=atan?(Gy/Gx). The spread function in this case is determined by the angle (Θ-Θ_0) instead of Θ in (9), where angles Θ and Θ0 are defined as in fig.8.[20] To be adaptive for different areas having different activity
levels, the standard deviation STD(I[m,n]) of the pixeles in window W with center in I[m,n] if used to control amplitude of the spread parameter σm in (9) as:

where STDmax and STDmin are the maximum and minimum value of all STD(I[m,n]) in current frame, respectively, σm – maximum value of spread parameter and γ - scaling factor in [0,1]. σm is scaled to γσ0 σ0 so fuzzy filter is applied with σm=γσ0 for areas with the lowest activity.[20] By adjusting σ0 and γ, the balance between edge preservation and artifact removal can be achieved.
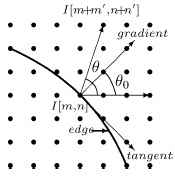 Fig 8 – Angles Θ and Θ0 of the edge-based directional fuzzy filter [20]
Fig 8 – Angles Θ and Θ0 of the edge-based directional fuzzy filter [20]
The proposed algorithm for edge-based directional fuzzy filtering is shown in fig.9. First, edge pixels are classified by comparing the gradient magnitude to an empirically determined threshold. Edge pixels are not be filtered because they are not ringing pixels. For nonedge pixels, if there are no edge pixels in the same block, the ringing artifacts in this block are not considered to be oriented in any particular direction and are filtered with an isotropic fuzzy filter. For the remaining nonedge pixels, the tangent angle of their nearest edge pixel is used to control the directional spread parameter.
 [20]
Fig. 9 – Algorithm of directional fuzzy filter
[20]
Fig. 9 – Algorithm of directional fuzzy filter
Conclusions
As the result model of directional adaptive fuzzy filter for processing grayscale images was implemented using MATLAB. Performed research confirmed effectiveness of filter model in reduction of the medium strength artifacts.
The work has not been finished yet. Further improvements of filter should be connected with attempts or improving it's functioning, in particular increasing filter's strength, or saving image edges. Probably filtering algorithms would be applied for non-standart images representation forms like using hexagonal pixels (instead of rectangular as usual). Further research also should be applied for true color images an videos processing.
References
- Jerri A., The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations. Dordrecht, The Netherlands: Kluwer, 1998.
- Kaneko M., Hatori Y, Koike A., “Improvements of transform coding algorithm for motion-compensated interframe prediction errors-DCT/SQ coding,” IEEE J. Sel Areas Commun., vol. 5, no. 8, pp. 1068–1078, Aug. 1987.
- Fan X., Gao W., Lu Y., Zhao D., “Flicking reduction in all intra frame coding,” Joint Video Team of ISO/IEC MPEG and ITU-T VCEG, JVT-E070, Oct. 2002.
- Sakaida S., Iguchi K., Gohshi S., Fujita Y., “Adaptive quantization control for reducing flicker of AVC/H.264 intra frames,” presented at the Picture Coding Symp., Dec. 2004.
- Jarske T., Haavisto P., Defee I., “Post-filtering methods for reducing blocking effects from coded images,” IEEE Trans. Cosum. Electron., vol. 40, no. 8, pp. 521–526, Aug. 1994.
- Nosratinia A., “Embedded post-processing for enhancement of compressed images,” in Proc. IEEE Data Compression Conf., 1999, pp. 62–71.
- Chen T., Wu H., Qiu B., “Adaptive postfiltering of transform coefficients for the reduction of blocking artifacts,” IEEE Trans. Circuits Syst. Video Technol., vol. 11, no. 5, pp. 594–602, May 2001.
- Liu S., Bovik A., “Efficient DCT-domain blind measurement and reduction of blocking artifacts,” IEEE Trans. Circuits Syst. Video Technol., vol. 12, no. 12, pp. 1139–1149, Dec. 2002.
- Gunturk B., Altunbasak Y., Mersereau R. M., “Multiframe blocking-artifact reduction for transform-coded video,” IEEE Trans. Circuits Syst. Video Technol., vol. 12, no. 4, pp. 276–282, Apr. 2002.
- Oguz S., Hu Y., Nguyen T., “Image coding ringing artifact reduction using morphological post-filtering,” in Proc. IEEE Int. Work. Multimedia Signal Processing, 1998, pp. 628–633.
- Kong H., Nie Y., Vetro A., Sun H., Barner K., “Adaptive Fuzzy Post-Filtering for Highly Compressed Video,” in Prof. IEEE Int. Conf. Image Proc., 2004, pp. 1802–1806.
- Westen S., Lagendijk R., Biemond J., “Adaptive spatial noise shaping for DCT based image compression,” in Proc. IEEE Int. Conf. Acoustics, Speech and Signal Processing, May 1996, vol. 4, pp. 2124–2127.
- DelCorso S., Miro C., Jung J., “MNR: A novel approach to correct MPEG temporal distortions,” IEEE Trans. Consum. Electron., vol. 49, no. 2, pp. 229–236, Feb. 2003.
- Leontaris A., Tonomura Y., Nakachi T., Cosman P., “Flicker suppression in JPEG2000 using segmentation-based adjustment of block truncation lengths,” in Proc. IEEE Int. Conf. Acoustics, Speech and Signal Processing, Apr. 2007, vol. 1, pp. 1117–1120.
- Smith S. M., Brady J.M., “Susan-a newapproach to lowlevel image processing,” Int. J. Comput. Vis., vol. 23, pp. 45–78, 1997.
- Tomasi C., Manduchi R., “Bilateral filtering for gray and color images,” in Proc. Int. Conf. Comput. Vis., 1998, p. 839846.
- Gelasca E. D., Ebrahimi T., “On evaluating metrics for video segmentation algorithms,” presented at the 2nd Int. Workshop on Video Processing and Quality Metrics for Consumer Applications, Jan. 2006.
- Nie Y., Barner K., “The fuzzy transformation and its application in image processing,” IEEE Trans. Image Process., vol. 15, no. 4, pp. 910–927, Apr. 2006.
- Justusson B., “Median filtering: Statistical properties,” in Two Dimensional Digital Signal Processing II, T. S. Huang, Ed. Berlin, Germany: Springer-Verlag, 1981.
- Vo D., Nguyen T., Yea S., Vetro A., "Adaptive Fuzzy Filtering for Artifact Reduction in Compressed Images and Videos", IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 18, NO. 6, JUNE 2009