Гуров Олексій Володимирович
Факультет комп'ютерних наук і технологій
Спеціальність "Програмне забезпечення автоматизованих систем"
Науковий керівник: доц., к.т.н. Зорі Сергій Анатолієвич
Реалістична стерео–візуалізація тривимірних сцен методом трасування променів на спеціалізованих паралельних обчислювальних системах
Алгоритм зворотного трасування променів
Огляд існуючих методів оптимізації алгоритму зворотного трасування променів
Огляд досліджень по темі в ДонНТУ
Огляд досліджень по темі у світі
Вступ
Розвиток сучасної техніки дозволяє розглядати на сьогоднішній день побудову стереозображень як одне з найбільш перспективних напрямків комп'ютерної графіки. Можливість стереопредставленія зображень породжує нові напрямки прикладних досліджень – створення програмно–апаратних комплексів віртуальної реальності, навчальних комплексів, побудову за допомогою стереозображень різних презентацій і анімацій. Існує кілька методів генерації реалістичних зображень, таких як пряма трасування променів (трасування фотонів), зворотнє трасування променів та інші. Методи трасування променів на сьогоднішній день вважаються найбільш потужними і універсальними методами створення реалістичних зображень.Відомо багато прикладів реалізації алгоритмів трасування для якісного відображення самих складних тривимірних сцен. Можна відзначити, що універсальність методів трасування в значній мірі обумовлена тим, що в їх основі лежать прості та ясні поняття, що відображають наш досвід сприйняття навколишнього світу [1]. Оточуючі нас об'єкти володіють по відношенню до світла такими властивостями:
– Випромінюють;
– Відбивають і поглинають;
– Пропускають крізь себе.
Кожне з цих властивостей можна описати деяким набором характеристик. Випромінювання можна охарактеризувати інтенсивністю та спектром. Властивість відображення (поглинання) можна описати характеристиками дифузного розсіювання і дзеркального відображення. Прозорість можна описати ослабленням інтенсивності і заломленням. З точок поверхні (обсягу) випромінюючих об'єктів виходять промені світла.Можна назвати такі промені первинними – вони висвітлюють все інше. Від джерел випромінювання виходить з різних напрямків незліченна безліч первинних променів. Деякі промені йдуть у вільний простір, а деякі потрапляють на інші об'єкти. Якщо промінь потрапляє в прозорий об'єкт, то, заломлюючись, він йде далі, при цьому деяка частина світлової енергії поглинається. У результаті дії на об'єкти первинних променів виникають вторинні промені.Деякі з них потрапляють на інші об'єкти. Так, багато разів відбиваючись і переломлюючи, окремі світлові промені приходять в точку спостереження.Таким чином, зображення сцени формується деякими безліччю світлових променів. Колір окремих точок зображення визначається спектром і інтенсивністю первинних променів джерел випромінювання, а також поглинанням світлової енергії в об'єктах, що зустрілися на шляху відповідних променів. Безпосередня реалізація даної променевої моделі формування зображення представляється скрутною. Можна спробувати побудувати алгоритм побудови зображення зазначеним способом. У такому алгоритмі необхідно передбачити перебір всіх первинних променів і визначити ті з них, які потрапляють в об'єкти і в камеру. Потім виконати перебір всіх вторинних променів, і також врахувати тільки ті, які потрапляють в об'єкти і в камеру. І так далі. Такий алгоритм називається прямий трасуванням променів. Головний недолік цього методу – багато зайвих операцій, пов'язаних з розрахунком променів, які потім не використовуються.
Актуальність теми
Побудова стереозображень є досить актуальним завданням на сьогоднішній день, тому що виникає питання максимальної правдоподібності та реалістичності комп'ютерних зображень. Метод трасування променів будує досить реалістичні зображення, але людина має об'ємний зір. Отже, стерео–візуалізація дасть більш правдоподібне зображення.
На сьогоднішній день реалізація трасування в реальному часі представляється скрутною. Відомі спроби створення 3D–прискорювачів з апаратною підтримкою алгоритму зворотного трасування, проте широкого поширення вони не отримали з–за відносно високої ціни і недостатнього швидкодії (задовільна швидкість побудови зображення була тільки для зображення з роздільною здатністю 640x480).>
Однак обчислювальні потужності персональних комп'ютерів зростають щодня.Незабаром повинні з'явитися машини, на яких алгоритм трасування буде працювати в реальному часі. Трасування повинна витіснити інші алгоритми за явної переваги в якості зображення і універсальності методу. але для цього необхідно передбачити прискорення алгоритму і його расспаралеліваніе.
Практичне застосування
1) Трасування променів в кіно:
Трасування променів в кіноіндустрії застосовується вже дуже давно і стала фактично стандартним методом візуалізації в цій галузі. Зрозуміло для завдань кіно необхідний фотореалістичний рендеринг. Швидкість в принципі не так важлива. Буває, що окремі послідовності кадрів розраховуються тижнями, і на обробку кадру йде більше 1 години (при 24 кадру / сек виходить, що 1 секунда буде рендерится 24 години).
2) Трасування променів в іграх:
У комп'ютерних іграх у трасування променів подвійне застосування. Розрахунок карт освітлення або лайтмапов. Зазвичай це робиться за допомогою фотонних карт. Практично будь–яка сучасна 3D гра використовує карти освітленості. Лайтмап – це текстура, на якій освітлення намальовано. Вона накладається поверх сцени і виходить, що сцена освітлена.
Друге застосування трасування променів в іграх – безпосередня візуалізація, попіксельно розрахунок зображення кожен кадр. Прикладів таких ігор можна привести трохи головним чином, тому що кількість пікселів досить велике і протрассировать мільйон променів 25 разів на секунду це досить непросте завдання. Вже зараз з'являються 8–ядерні машини в якості ПК, обчислювальних потужностей яких у принципі вистачає для візуалізації середньої сцени методом зворотного трасування променів.
3) Трасування променів у торговельному бізнесі:
В основному мова йде про фотореалістичної візуалізації. Часто деякий товар, наприклад, меблі є в декількох варіантах. У офісних крісел може бути різна оббивка, колеса або інші деталі, з яких по–суті можна зібрати потрібну покупцю крісло. Проте займатися цим на місці не завжди зручно. Частіше набагато дешевше / простіше змоделювати той товар, який покупець хоче бачити. За допомогою методу трасування променів можна отримати практично неможливо відрізнити від реальності картинку – тобто можна зробити фотографію товару, якого ще немає [2].
Алгоритм зворотного трасування променів
Метод зворотного трасування променів дозволяє значно скоротити перебір світлових променів. Метод розроблений у 80–х роках, основоположними вважаються роботи Уіттеда і Кея. Відповідно до цього методу відстеження променів виробляється не від джерел світла, а у зворотному напрямку – від точки спостереження. Так враховуються тільки ті промені, які вносять вклад у формування зображення. Площина проектування розбита на безліч пікселів. Виберемо центральну проекцію з центром сходу на деякій відстані від площини проектування.Проведемо пряму лінію з центру сходження через середину піксела площині проектування. Це буде первинний промінь зворотного трасування. Якщо цей промінь потрапить в один або декілька об'єктів сцени, то вибираємо найближчу точку перетину. Для визначення кольору пікселя зображення потрібно враховувати властивості об'єкта, а також те, яке світлове випромінювання припадає на відповідну точку об'єкта.
Якщо об'єкт дзеркальний (хоча б частково), то будуємо вторинний промінь – промінь падіння, вважаючи променем відображення попередній, первинний трассируемого промінь. Для ідеального дзеркала досить потім простежити лише чергову точку перетину вторинного променя з деяким об'єктом. У ідеального дзеркала ідеально рівна відполірована поверхня, тому одному відбитому променю відповідає тільки один падаючий промінь. Дзеркало може бути затемненим, тобто поглинати частина світлової енергії, але все одно залишається правило: один промінь падає – один відбивається.
Якщо об'єкт прозорий, то необхідно побудувати новий промінь, такий, який при ламанні давав би попередній трассируемого промінь. Для дифузного відбиття інтенсивність відбитого світла, як відомо, пропорційна косинусу кута між вектором променя від джерела світла і нормаллю. Коли з'ясовується, що поточний промінь зворотного трасування не перетинає який–небудь об'єкт, а йде у вільний простір, то на цьому трасування для цього променя закінчується.
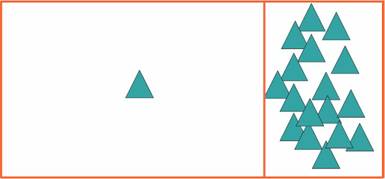
При практичній реалізації методу зворотного трасування вводять обмеження.Деякі з них необхідні, щоб можна було в принципі вирішити завдання синтезу зображення, а деякі обмеження дозволяють значно підвищити швидкодію трасування [2]. Алгоритм виглядає наступним чином: з віртуального очі через кожен піксель зображення випускається промінь і знаходиться точка його перетину з поверхнею сцени. Промені, випущені з ока називають первинними. Припустимо, первинний промінь перетинає якийсь об'єкт 1 в точці H1 (рис. 1).
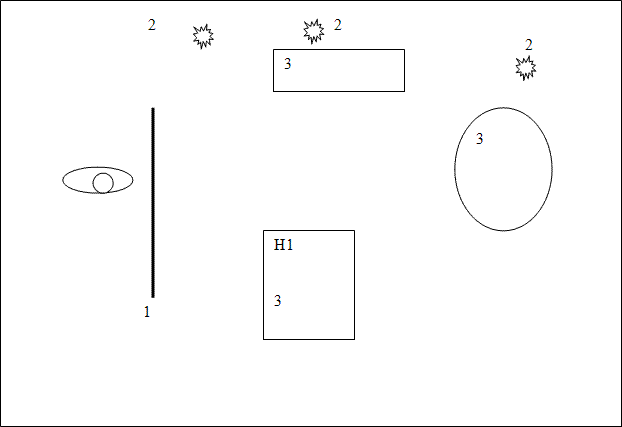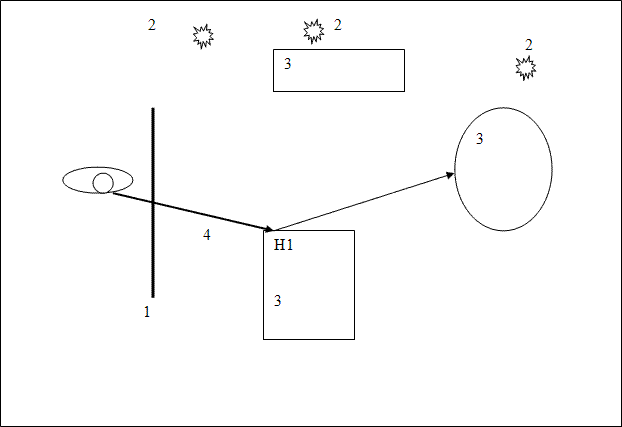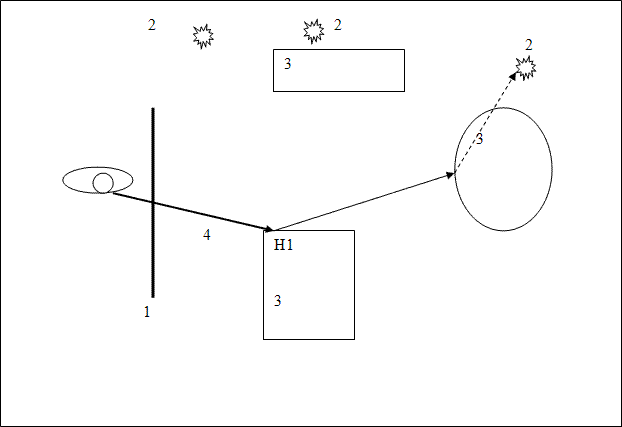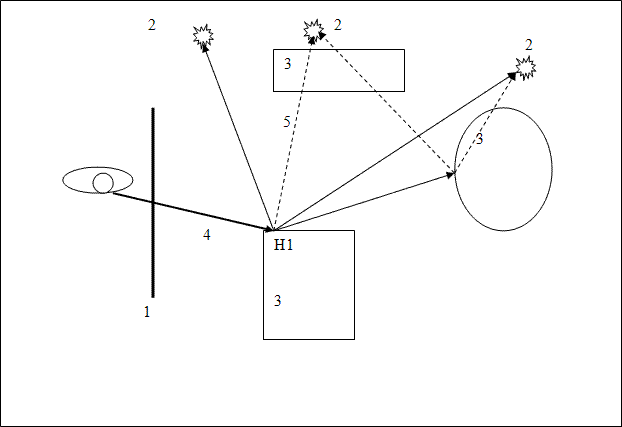
Рисунок 1 – Візуалізація алгоритму трасування променів. Анімація складається з 6 кадрів з затримкою 1 с. Кількість циклів відтворення обмежена 5
1–зображення, 2–джерело світла, 3–об'єкт, 4 – промінь з ока, 5 – промінь тіні
Далі необхідно визначити для кожного джерела освітлення, чи видно з нього ця крапка. Припустимо поки, що всі джерела світла точкові. Тоді для кожного точкового джерела світла, до нього випускається тіньової промінь з точки H1. Це дозволяє сказати, висвітлюється дана точка конкретним джерелом. Якщо тіньової промінь знаходить перетин з іншими об'єктами, розташованими ближче ніж джерело світла, значить, точка H1 знаходиться в тіні від цього джерела і висвітлювати її не треба. Інакше, вважаємо освітлення за деякою локальної моделі (Фонг, Кук–Торранс і.т.д.). Освітлення з усіх видимих (з точки H1) джерел світла складається. Далі, якщо матеріал об'єкта 1 має відображають властивості, з точки H1 випускається відбитий промінь і для нього вся процедура трасування рекурсивно повторюється. Аналогічні дії мають бути виконані, якщо матеріал має преломляющие властивості [2].
Огляд існуючих методів оптимізації алгоритму зворотного трасування променів
Існує безліч підходів до оптимізації алгоритму зворотного трасування променів.Далі представлені деякі варіанти прискорення роботи алгоритму.
1 kd–tree
Даний підхід до оптимізації методу трасування променів розглядаються в роботах [3–6]. Розглянемо структуру бінарного просторового розбиття, звану kd–дерево. Ця структура є бінарне дерево обмежують паралелепіпедів, вкладених один в одного. Кожен паралелепіпед у kd–дереві розбивається площиною, перпендикулярної однієї з осей координат на два дочірніх паралелепіпеда. Вся сцена цілком міститься всередині кореневого паралелепіпеда, але, продовжуючи рекурсивне розбиття паралелепіпедів, можна прийти до того, що в кожному листовому паралелепіпеді буде міститися лише невелика кількість примітивів. Таким чином, kd–дерево дозволяє використовувати бінарний пошук для знаходження примітиву, які перетинаються променем.
1 Побудова kd–дерева Алгоритм побудови kd–дерева можна представити таким чином. Далі по тексту прямокутний паралелепіпед будемо називати "бокс" (box).
1) "Додати" всі примітиви в обмежує бокс. Тобто побудувати обмежує всі примітиви бокс, який буде відповідати кореневого вузла дерева.
2) Якщо примітивів у вузлі мало або досягнуть межа глибини дерева, завершити побудову.
3) Вибрати площину розбиття, яка ділить даний вузол на два дочірніх. Будемо називати їх правим і лівим вузлами дерева.
4) Додати примітиви, пересічні з боксом лівого вузла в лівий вузол, примітиви, пересічні з боксом правого вузла в правий.
5) Для кожного з вузлів рекурсивно виконати даний алгоритм починаючи з кроку 2.
Найскладнішим у побудові kd–дерева є третім крок. Від нього безпосередньо залежить ефективність прискорюючою структури. Існує кілька способів вибору площині розбиття, розглянемо їх по порядку:
1. Вибрати площину розбиття по центру. Найпростіший спосіб – вибирати площину по центру боксу. Спочатку вибираємо вісь (x, y або z), в якій бокс має максимальний розмір, потім розбиваємо бокс по центру (рис 2).
Рисунок 2 – Розбиття по центру
Цей спосіб має погану адаптивність. Інтуїтивно можна описати причину поганої швидкості на таких деревах тим, що в кожному вузлі досить багато пустого простору, через яке промінь трасує (проходить через дерево під час пошуку) в той час як порожній простір має одразу ж по–можливості відкидатися.
2. Вибрати площину по медіані.
Можна подумати, що було б непогано розділяти вузол на два дочірніх кожен раз так, щоб у правому та лівому піддереві кількість примітивів було однаково. Таким чином ми побудуємо збалансоване дерево, що має прискорити пошук (рис 3).
Рисунок 3– Розбиття по медіані
Це не дуже вдала ідея. Вся справа в тому, що збалансовані дерева можуть допомогти тільки якщо шуканий елемент кожного разу знаходиться у випадковому вузлі, тобто якщо розподіл променів по вузлах під час пошуку буде рівномірно. У дійсності, це не так. Променів у середньому піде більше в той вузол, який більше за своєю площею поверхні, а при медіанної розбитті ці площі у вузлів можуть бути різні.
2. Surface Area Heuristic (SAH)
Які ж критерії добре–побудованого kd–дерева? На інтуїтивному рівні це насправді це не дуже зрозуміло, хоча вираз "якомога більше порожнього простір повинен бути відкинуто як можна швидше" напевно підійде. Введемо функцію вартості простежування (cost traversal), яка буде відображати, наскільки дорого по обчислювальних ресурсів простежувати даний вузол випадковим набором променів. Будемо обчислювати її за такою формулою.
Де CostEmpty – вартість простежування порожнього вузла (деяка константа), SurfaceArea – площа поверхні відповідного вузла, а N – число примітивів у ньому.Потрібно вибирати площину разбіеніея так, щоб мінімізувати цю функцію.Аргумент функції x є одномірної координатою площині розбиття.
Добрими кандидатами на мінімум SAH можуть служити кордону примітивів.Простий алгоритм побудови виглядає наступним чином. Кожного разу при виборі площині потрібно перебрати всілякі межі примітивів за трьома вимірами, обчислити в них значення функції вартості і знайти мінімум серед усіх цих значень.Коли ми обчислюємо SAH для кожної площині, то нам необхідно знати N (left) і N (right) – кількості примітивів праворуч і ліворуч від площини. Якщо обчислювати N простим перебором, у результаті вийде квадратичний по складності алгоритм побудови [3] (рис. 4).
Рисунок 4 – Розбинття з урахуванням SAH
Огляд досліджень по темі в ДонНТУ
У ДонНТУ даною тематикою займалися Іванова Катерина, Сереженко Олександр, Винокуров Олексій и Грищенко Олександр.
Огляд досліджень по темі у світі
Методами оптимізації та прискорення алгоритму трасування променів для отримання фото реалістичних зображень займаються світові відомі компанії, які спеціалізуються на розробці візуальних ефектів, створення мультфільмів (PIXAR), компанії, які спеціалізуються на розробці апаратного забезпечення для ПК (INTEL, nVidia, AMD), компанії, які спеціалізуються на розробці спеціалізованого комп'ютерного обладнання (Caustic, Splutterfish). Через те, що метод трасування променів дуже вимогливий до апаратної складової, навіть світовий лідер зі створення візуальних мультфільмів PIXAR використовує цю технологію не для всіх розробок, щоб не перевантажити існуючі обчислювальні потужності. Аналогічну ситуацію відчуває компанія Lucas Arts [7].
Основні цілі
– Розробити оптимізований алгоритм трасування променів, з метою зменшення обчислювальної складності;
– Модифікувати розроблений алгоритм для стерео–візуалізації;
– Дослідити можливість реалізації алгоритму на паралельних архітектурах обчислювальних систем, включаючи архітектури GPU сучасних відеокарт ПК;
– Створити прототип програмної системи для синтезу реалістичних стереозображень з використанням методу трасування променів на паралельній архітектурі GPU відеокарт ПК, проаналізувати характеристики процесу синтезу в порівнянні з «класичним» рішенням завдання.
Висновки
У ході проведення дослідження проблеми були проаналізовані існуючі підходи до прискорення реалізації методу трасування променів, виявлені їх сильні і слабкі сторони, розглянуті методи створення стерео–зображень. На сьогоднішній день реалізація трасування в реальному часі потребує багато обчислювальних ресурсів.
Однак обчислювальні потужності персональних комп'ютерів та їх спеціалізованих підсистем зростають щодня. Трасування повинна витіснити інші алгоритми за явної переваги в якості зображення і універсальності методу. Отже, можливість ефективної за швидкістю реалізації реалістичного синтезу стереоскопічних зображень методом трасування променів і можливість його реалізації на паралельних архітектурах спеціалізованих обчислювальних систем є важливим завданням.
Література
- Михайлюк М.В., Хураськин И.А. Синтез стереоизображения для систем виртуальной реальности с использованием оптической трекинговой системы.
- Трассировка лучей, МГУ, 2007 [Электронный ресурс].–Режим доступа: http://www.ray–tracing.ru/
- Shevtsov M., Soupikov A., Kapustin A. Highly Parallel Fast KD–tree Construction for Interactive Ray Tracing of Dynamic Scenes. In Proceedings of the EUROGRAPHICS conference, 2007
- Foley T., Sugerman J. KD–Tree Acceleration Structures for a GPU Raytracer. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, p. 15–22, 2005.
- Horn D., Sugerman J., Houston M., Hanrahan P. Interactive k–D Tree GPU Raytracing. Proceedings of the symposium on Interactive 3D graphics and games on Fast rendering, p. 167–174, 2007.
- Popov S., Gunther J., Seidel H.–P., Slusallek P. Stackless KD–Tree Traversal for High Performance GPU Ray Tracing. In Proceedings of the EUROGRAPHICS conference, 2007.
- Сайт магистра ДонНТУ Сереженко А А – Разработка ускоренного алгоритма трассировки лучей [Электронный ресурс].–Режим доступа: http://masters.donntu.ru/2010/fknt/serezhenko/diss/index.htm
- Интерактивная трассировка лучей с использованием SIMD инструкций, 2008 [Электронный ресурс].– Режим доступа: http://software.intel.com/ru–ru/articles/interactive–ray–tracing/
- Андреев С.В., Бондарев А.Е., Михайлова Т.Н., Рыжова И.Г. Организация стереопредставлений в задачах синтеза фотореалистичных изображений и научной визуализации, Москва, 2010.
- Michael Doneus, Klaus Hanke, ANAGLYPH IMAGES – STILL A GOOD WAY TO LOOK AT 3D–OBJECTS?
Важливе зауваження
При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2011 р. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.