Климова Екатерина Александровна

Факультет компьютерных наук и технологий

Кафедра компьютерных систем мониторинга

Специальность: Компьютерный эколого-экономический мониторинг

Тема выпускной работы:

Разработка дифференциальной математической модели эволюции метеопараметров и решение задач прогноза на ее основе

Научный руководитель: Беловодский Валерий Николаевич

 

Реферат

по теме магистерской работы

«Разработка дифференциальной математической модели эволюции метеопараметров и решение задач прогноза на ее основе»

Актуальность темы

«Завтра ожидают метель, снежные заносы, аномальный мороз и штормовой ветер, который временами будет достигать 15 метров в секунду. Местами метель с порывами ветра до 15-17 метров в секунду и ухудшением видимости». Такие прогнозы, как этот, дают критически важную информацию об изменении погоды.

В тяжелых погодных условиях краткосрочные прогнозы могут спасти жизни людей и сократить материальные убытки. Очень важно, чтобы прогнозы погоды были как можно более точными. Каждый год в мире стихийные бедствия уносят около 250 тысяч человеческих жизней. Размер ущерба, наносимого имуществу, лежит в пределах 50-100 млрд. долларов США. Но мировая статистика показывает, если доверять гидрометеорологической информации и адекватно на нее реагировать, то можно предотвратить от 30 до 40% потерь и полностью избежать человеческих жертв [1].

Надежный прогноз погоды является ключом для социально-экономического развития и имеет важное значение для безопасности человеческого общества. Прогнозы используются правительством и промышленностью в целях защиты жизни и имущества.

Данные прогноза погоды не менее важны и для сельского хозяйства. Анализ имеющихся данных показывает, что по крайней мере 50% изменчивости урожайности связано с погодой. Потери урожая могут быть существенно снижены путем корректировки с помощью своевременных и точных прогнозов погоды [2].

Прогнозирование погоды также является очень важным для таких областей человеческой деятельности, как: авиация, судоходство, рыболовство. Возрастание точности прогноза погоды является прямым следствием технического прогресса, новых подходов используемых для прогнозирования, улучшения средств наблюдения и сбора данных. Улучшение стало возможным в значительной мере за счет роста возможностей компьютеров (появления высокоскоростных компьютеров), которые необходимы для проведения огромного количества вычислений.

Цели и задачи

Цель дипломной работы – изучить методы, применяемые для прогнозирования погоды, разработать программный проект, включающий методику составления краткосрочных прогнозов погоды.

Объектом исследования являются временные ряды метеопараметоров.

Предмет исследования – модели прогнозирования, качество и дальность их результатов.

Задачи магистерской работы:

• Изучение существующих методов используемых для прогнозирования метеопараметров по временным рядам;
• Разработка математической модели, позволяющей производить прогноз метеопараметров;
• Оценка адекватности и точности разработанной модели.

Предполагаемая научная новизна

Научная новизна исследований заключается в использовании для прогнозирования метеопараметров дифференциальных уравнений, правыми частями которых, являются нейронные сети. В формировании дифференциальной математической модели динамики метеопараметров, использующих дифференциальные уравнения, принимала участие размерность модели полученная с помощью алгоритма Грассбергера-Прокаччиа.

Обзор исследований по теме в ДонНТУ

На кафедре КСМ в течение последних двух лет магистрами Гриценкой А.В. и Сивяковым А.С. была разработана программная система Fcomplex, предназначенная для краткосрочного прогнозирования метеопараметров по временным рядам с использованием конечных математических моделей. Прогнозирование осуществляется на базе временных рядов, снимаемых с метеостанции Vantage Pro 2. Fcomplex - это программная система для составления краткосрочных прогнозов значений метеопараметров «Температура», «Давление», «Влажность» и «Скорость ветра» с заблаговременностью 1, 3, 6 и 9 часов. Для определения размерности модели в ней используются методы главных компонент и ложных соседей, для построения аппроксимирующих зависимостей – искусственные нейронные сети и метод Эглайса [3, 4].

Апробация

Результаты работы докладывались на II всеукраинской научно-технической конференции студентов, аспирантов и молодых ученных «Информационные управляющие системы и компьютерный мониторинг» 11-13 апреля 2011 г. и опубликованы в соответствующем сборнике.

Текущие и планируемые результаты

В данной работе расчет прогноза предполагается проводить путем выполнения следующих этапов:

1. получение временного ряда из базы данных, содержащей данные снимаемые с метеостанции Vantage Pro 2;
2. анализ данных;
3. определение размерности модели;
4. прогнозирование;
5. проверка эффективности модели.

Рисунок 1 – Алгоритм модели прогнозирования (анимация: объем – 88,0 КБ; размер – 400x500; количество кадров – 6; бесконечное число циклов повторения; задержка между кадрами – 1 с; задержка между последним и первым кадром – 1 мс)

Рассмотрим более подробно каждый этап.

Этап № 1. На этом этапе происходит получение временных рядов выбранной метеовеличины из базы данных, содержащей информацию, которая передается с метеостанции Vantage Pro 2 с временным интервалом в 10 минут по следующим показателям: температура, влажность, давление, скорость и направление ветра [3].

Этап № 2. На этом этапе происходит предварительный анализ данных, а именно, сглаживание с помощью скользящего среднего.

Обычно, сглаживание временного ряда осуществляется с целью уменьшения ошибки исходных данных, в частности – уменьшения случайного шума, полученного при измерении на метеостанции. По своей сути, сглаживание представляет собой, своего рода, усреднение в результате чего случайные составляющие в компонентах временного ряда взаимно поглощают друг друга [5].

С целью нахождения наилучшего метода сглаживания нами были проведены эксперименты по сглаживанию различных метеорядов. Было проведено экспоненциальное сглаживание временных рядов и сглаживание с использованием скользящей средней, а также, была вычислена средняя относительная ошибка сглаживания. Эксперименты показали, что средняя относительная ошибка при экспоненциальном сглаживании возрастает с увеличением длины временного ряда, и превышает среднюю относительную ошибку при сглаживании простым средним. На основании этого в дальнейшем предполагается использовать сглаживание скользящей средней [3].

Этап №3. На этом этапе определяется наименьшая размерность модели, обеспечивающая однозначность прогноза.

Один из наиболее важных открытий за последние несколько десятилетий является то, что случайное поведение системы может быть описано как поведение детерминированной нелинейной системы.

Динамическую систему можно представить как объект любой природы, состояние которого изменяется во времени в соответствии с некоторым динамическим законом [6].

Теоретический фундамент к применению методов анализа динамических систем заложен теоремой Такенса. Суть этой теоремы заключается в том, что по динамике одного временного ряда можно судить обо всей эволюции динамической системы [7].

Для определения размерности модели существуют различные методы. Это, в частности: методы ложных соседей, главных компонент, Грассбергера-Прокаччиа, хорошо приспособленного базиса и другие [1].

Для определения размерности модели в дальнейшем предполагается использовать метод Грассбергера-Прокаччиа. Одним из главных достоинств метода является простота реализации [3].

Метод Грассбергера-Прокаччиа является одним из самых распространенных для определения корреляционной размерности. Корреляционная размерность показывает число пар точек, достаточных для определения состояния динамической системы [8].

Воспользовавшись идеей метода запаздывания реконструкции аттрактора нужно преобразовать временной ряд в m-мерное пространство:

где τ – временная задержка (временной лаг), m – размерность пространства вложения.

Временная задержка τ определяется равной времени первого пересечения нуля автокорреляционной функцией. Она определяется как:

Для определения размерности модели вычисляется корреляционный интеграл C(е), показывающий относительное число пар точек аттрактора, находящихся на расстоянии, не большем е:

где i ≠ j, е – размер ячейки (ограничено минимальным расстоянием между ближайшими точками аттрактора, и размером аттрактора). Q – функция Хевисайда, т.е.

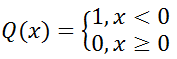
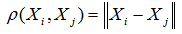– расстояние в m-мерном фазовом пространстве,

где N – число точек X_i на аттракторе.

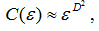
D₂ – корреляционная размерность аттрактора.

По сути, С(е) – зависимость количества точек аттрактора в m-мерном пространстве, расстояние между которыми меньше е, от размера разрешающей ячейки, отнесенному к полному количеству пар точек [8].

Для определения размерности: строится график (log(С(е)), log(е)) в двойном логарифмическом масштабе; выделяются линейные участки построенных кривых; производится их аппроксимация по методу наименьших квадратов; размерность определяется как тангенс угла наклона прямой, аппроксимирующей график корреляционного интеграла C(е).

Количественную оценку точности нахождения корреляционной размерности предложили Экман и Рюэль (1981). Обозначим через е_max – максимальный размер элементарной ячейки, а е_min – её минимальный размер, которые соответствуют началу и концу линейного участка зависимости С(е) от е в двойном логарифмическом масштабе. Тогда p = е_max/е_min . Для надежного измерения D₂ необходимо p=10. Также одно из основных условий данной оценки заключается в соблюдении неравенства D₂<2lgN, где N – длина временного ряда [8].

Этап № 4. На этом этапе формируется математическая модель процесса в виде дифференциального уравнения и осуществляется прогноз.

Основным математическим аппаратом нелинейной динамики являются, как правило, дифференциальные уравнения. Именно на их основе в данной работе предполагается осуществлять прогноз, а именно, правые части этих уравнений описывать с помощью нейронных сетей [9].

Дифференциальные уравнения являются основным математическим аппаратом нелинейной динамики, они применяются в качестве основного прогностического инструмента и в данной работе. Именно, с их помощью можно описывать эволюцию системы и прогнозировать ее поведение в следующие моменты времени.

Опыт показывает, что искусственные нейронные сети нередко оказываются более эффективными, чем классические методы прогнозирования. Они дают более точный результат и позволяют работать с зашумленными и неточными данными. Нейронная сеть не прогнозирует будущее, она пытается найти текущее состояние системы в раннее встречающихся ситуациях и максимально точно воспроизвести результат [3, 10].

Именно поэтому для прогноза выбираются обыкновенные дифференциальные уравнения:

dx/dt=f(x,c)

где x – D-мерный вектор состояния, f – вектор – функция, с – Р-мерный вектор параметров, t – непрерывное время.

Определяется вид функций f с использованием метода сильной аппроксимации –искусственных нейронных сетей.

С использованием программной системы Fcomplex были проведены эксперименты с тремя видами сетей: линейной, нелинейной и регрессионной. Эксперименты показали, что наилучший прогноз для дальности прогнозирования 1, 3, 6, 9 часов дает нелинейная сеть.

В данном случае, нелинейная сеть представляет собой один скрытый слой (от 1 до 10 нейронов) с функцией активации гиперболического тангенса и выходным слоем, содержащим 1 нейрон с линейной функцией активации. На рисунке 2 представлена структура нелинейной сети [11].

Рисунок 2 – Архитектура искусственной нейронной сети (анимация: объем - 126,0 КБ; размер – 500x277; количество кадров – 7; бесконечное число циклов повторения; задержка между кадрами – 0,5 с; задержка между последним и первым кадром – 0,5 с)

Сеть не содержит обратных связей, нейроны соединяются по принципу «каждый с каждым». Оба слоя имеют смещения. Веса и смещения настраиваются методом Левенберга-Марквардта, критерий качества обучения – средняя квадратичная ошибка [3].

Математическое описание модели имеет вид:

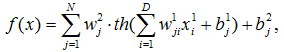
где параметром функции f является временной ряд x.

То есть, прогноз предполагается осуществлять с помощью модели:

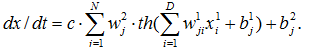
Этап №5. На этом этапе происходит проверка эффективности модели. Эффективность модели определяется её целями. Так как целью модели является прогноз метеопараметров, то лучшей проверкой эффективности будет сравнение полученных прогнозных значений с истинными значениями метеопараметров.

Заключение

Результат магистерской работы – модель прогнозирования метеопараметров с использованием временных рядов. Данные исследования и вычисления могут стать полезными для метеорологов и быть использованы для дальнейших исследований и усовершенствований в этой области.

При написании данного автореферата магистерская работа ещё не завершена. Окончательное завершение: декабрь 2011 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Литература

1. Гриценко А.В. Реконструкция уравнений и прогнозирование метеопараметров по их временным рядам. [Текст] – Донецк, ДонНТУ, 2010. – 149 с.
2. Importance of weather forecasting. [Electronic resourse] / Интернет-ресурс. – Режим доступа:http://vasat.icrisat.org/?q=node/300
3. Климова Е.А., Беловодский В.Н. Дифференциальная математическая модель эволюции метеопараметров. [Текст] – Компьютерный мониторинг и информационные технологии 2011 / Материалы I всеукраинской научно-технической конференции, аспирантов и молодых ученых. – Донецк, ДонНТУ – 2011.
4. Сивяков А. С. Построение прогностического комплекса и внедрения его в электронную сеть университета. [Текст] – Донецк, ДонНТУ, 2011. – 125 с.
5. Исследователь. [Electronic resourse] / Интернет-ресурс. – Режим доступа: http://ligis.ru/effects/stat/modules/sttimser.html – Анализ временных рядов.
6. Чечурин А.В. Исследование алгоритмов оценки размернсоти реконструкции аттракторов [Текст] / Чечурин А.В. // Задачи системного анализа, управления и обработки информации. Межвузовский сборник научных трудов. Вып. 1.— М.: МГУП, 2006. - С.15-23
7. Гудков Г.В. Диагностические возможности определения детерменированного хаоса в структуре вариабельности ритма сердца плода [Electronic resourse] / Интернет-ресурс. – Режим доступа:http://vestnik.kmldo.ru/pdf/08/01/02.pdf
8. Антипов О.И., Неганов В.А. Фрактальный анализ нелинейных систем и построение на его основе прогнозирующих нейронных сетей [Текст] / О. И. Антипов, В. А. Неганов // Физика волновых процессов и радиотехнические системы. - 2010. - Т. 13, N 3. - С. 54-63
9. Козлов Д.А. Методы нелинейной динамики в моделировании макро-экономических процессов [Electronic resourse] / Интернет-ресурс. – Режим доступа: http://www.ecfor.ru/pdf.php?id=books/kor001/09
10. Безручко, Б.П. Математическое моделирование и хаотические временные ряды [Текст] / Б.П. Безручко, Д.А. Смирнов // Саратов: ГосУНЦ «Колледж», 2005. – С. 320.
11. Медведев В.С. Нейронные сети. MaTLab 6/ Медведев В.С., Потемкин В.Г. [Под общ. ред. к.т.н. В.Г. Потемкина]. – М.: ДИАЛОГ-МИФИ, 2002. 496 с.