Магістр ДонНТУ Климова Катерина Олександрівна

Климова Катерина Олександрівна

Факультет комп'ютерних наук і технологій

Кафедра комп'ютерних систем моніторинга

Спеціальність: Комп'ютерний еколого-економічний моніторинг


Тема випускної роботи:

Розробка диференціальної математичної моделі еволюції метеопараметров і вирішення завдань прогнозу на її основі

Керівник: Бєловодський Валерій Миколайович

 

Реферат за темою

магістерської роботи:

“Розробка диференціальної математичної моделі еволюції метеопараметров і вирішення завдань прогнозу на її основі”



Актуальність теми

“Завтра очікується хуртовина, снігові замети, аномальний мороз і штормовий вітер, який часом буде досягати 15 метрів на секунду. Місцями хуртовина з поривами вітру до 15-17 метрів на секунду і погіршенням видимості”. Такі прогнози, як цей, дають критично важливу інформацію про зміну погоди.

У важких погодних умовах короткострокові прогнози можуть врятувати життя людей і скоротити матеріальні збитки. Дуже важливо, щоб прогнози погоди були як можна більш точними. Кожен рік у світі стихійні лиха забирають близько 250 тисяч людських життів. Розмір збитку, що наноситься майну, лежить в межах 50-100 млрд. доларів США. Але світова статистика показує, якщо довіряти гідрометеорологічної інформації і адекватно на неї реагувати, то можна запобігти від 30 до 40% втрат і повністю уникнути людських жертв [1].

Надійний прогноз погоди є ключем для соціально-економічного розвитку і має важливе значення для безпеки людського суспільства. Прогнози використовуються урядом і промисловістю, з метою захисту життя і майна.

Дані прогнозу погоди не менш важливі і для сільського господарства. Аналіз наявних даних показує, що принаймні 50% мінливості врожайності пов'язано з погодою. Втрати врожаю можуть бути істотно знижені шляхом коригування за допомогою своєчасних і точних прогнозів погоди [2].

Прогнозування погоди також є дуже важливим для таких галузей людської діяльності, як: авіація, судноплавство, рибальство. Зростання точності прогнозу погоди є прямим наслідком технічного прогресу, нових підходів використовуваних для прогнозування, поліпшення засобів спостереження і збору даних. Поліпшення стало можливим значною мірою за рахунок зростання можливостей комп'ютерів (появи високошвидкісних комп'ютерів), які необхідні для проведення величезної кількості обчислень.

Цілі і завдання

Мета дипломної роботи – вивчити методи, які застосовуються для прогнозування погоди, розробити програмний проект, що включає методику складання короткострокових прогнозів погоди.

Об'єктом дослідження є часові ряди метеопараметерів.

Предмет дослідження є моделі прогнозування, якість і дальність їх результатів.

Завдання магістерської роботи:

  • Вивчення існуючих методів використуємих для прогнозування метеопараметрів по часовим рядам;
  • Розробка математичної моделі, що дозволяє робити прогноз метеопараметрів;
  • Оцінка адекватності і точності розробленої моделі.

Передбачувана наукова новизна

Наукова новизна досліджень полягає в використанні диференціальних рівнянь, правими частинами яких, є нейронні мережі для прогнозування метеопараметрів. У формуванні диференціальної математичної моделі динаміки метеопараметрів, що використовують диференціальні рівняння, брала участь розмірність моделі отримана за допомогою алгоритму Грассбергера-Прокаччіа.

Огляд досліджень по темі в ДонНТУ

На кафедрі КСМ протягом останніх двох років магістрами Гриценко А.В. та Сивяковим А.С. була розроблена програмна система Fcomplex, призначена для короткострокового прогнозування метеопараметрів по часовим рядам з використанням кінцевих математичних моделей. Прогнозування здійснюється на базі часових рядів, що знімаються з метеостанції Vantage Pro 2. Fcomplex – це програмна система для складання короткострокових прогнозів значень метеопараметрів “Температура”, “Тиск”, “Вологість” та “Швидкість вітру” із завчасністю 1, 3, 6 та 9 годин. Для визначення розмірності моделі в ній використовуються методи головних компонент та помилкових сусідів, для побудови апроксимуючих залежностей – штучні нейронні мережі та метод Еглайса [3, 4].

Апробація

Результати роботи доповідалися на II всеукраїнській науково-технічній конференції студентів, аспірантів та молодих вчених “Інформаційні управляючі системи та комп'ютерний моніторинг” 11-13 квітня 2011 р. і опубліковані у відповідному збірнику.

Поточні і плановані результати

У даній роботі розрахунок прогнозу передбачається проводити шляхом виконання наступних етапів:

  1. отримання часового ряду з бази даних, що містить дані, які знімаються з метеостанції Vantage Pro 2;
  2. аналіз даних;
  3. визначення розмірності моделі;
  4. прогнозування;
  5. перевірка ефективності моделі.

Розглянемо більш детально кожен етап.

Етап № 1. На цьому етапі відбувається отримання часових рядів обраної метеовеличин з бази даних, що містить інформацію, яка передається з метеостанції Vantage Pro 2 з часовим інтервалом в 10 хвилин за наступними показниками: температура, вологість, тиск, швидкість і напрямок вітру [3].

Етап № 2. На цьому етапі відбувається попередній аналіз даних, а саме, згладжування за допомогою змінного середнього.

Зазвичай, згладжування часового ряду здійснюється з метою зменшення помилки вихідних даних, зокрема – зменшення випадкового шуму, отриманого при вимірюванні на метеостанції. За своєю суттю, згладжування представляє собою, свого роду, усереднення в результаті чого випадкові складові в компонентах часового ряду взаємно поглинають один одного [5].

З метою знаходження найкращого методу згладжування нами були проведені експерименти зі згладжування різних метеорядів. Було проведено експоненціальне згладжування часових рядів і згладжування з використанням змінної середньої, а також, була обчислена середня відносна помилка згладжування. Експерименти показали, що середня відносна помилка при експоненційному згладжуванні зростає із збільшенням довжини часового ряду, і перевищує середню відносну помилку при згладжуванні простим середнім. На підставі цього надалі передбачається використовувати згладжування за допомогою змінної середньої [3].

Етап № 3. На цьому етапі визначається найменша розмірність моделі, що забезпечує однозначність прогнозу.

Одним з найбільш важливих відкриттів за останні кілька десятиліть є те, що випадкове поводження системи може бути описане детермінованою нелінійної системою.

Динамічну систему можна представити як об'єкт будь-якої природи, стан якого змінюється в часі відповідно до деякого динамічного закону [6].

Теоретичний фундамент до застосування методів аналізу динамічних систем закладений теоремою Такенса. Суть цієї теореми полягає в тому, що за динамікою одного часового ряду можна судити про всю еволюції динамічної системи [7].

Для визначення розмірності моделі існують різні методи. Це, зокрема: методи помилкових сусідів, головних компонент, Грассбергера-Прокаччіа, добре пристосованого базису [1].

Для визначення розмірності моделі надалі передбачається використовувати метод Грассбергера-Прокаччіа. Одним з головних достоїнств методу є простота реалізації [3].

Метод Грассбергера-Прокаччіа є одним з найпоширеніших для визначення кореляційної розмірності. Кореляційна розмірність показує число пар точок, достатніх для визначення стану динамічної системи [8].

Скориставшись ідеєю методу запізнювання реконструкції аттрактора потрібно перетворити часової ряд у m-мірний простір:

Метод часового запізнювання

де τ – часова затримка (часовий лаг), m – розмірність простору вкладення.

Часова затримка τ визначається як час першого перетину нуля автокорреляційнною функцією. Вона визначається як:

Для визначення розмірності моделі обчислюється кореляційний інтеграл C (е), що показує відносне число пар точок атрактора, що знаходяться на відстані, не більшій е:

де i ≠ j, е – розмір комірки (обмежений мінімальною відстанню між найближчими точками аттрактора, і розміром аттрактора). Q – функція Хевісайда, тобто

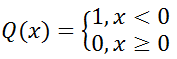
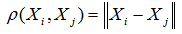– відстань у m-мірному фазовому просторі,

де N – кількість точок Xi на аттракторі.

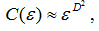
D2 – кореляційна розмірність атрактора.

Для визначення розмірності: будується графік (log(С(е)), log(е)) в подвійному логарифмічному масштабі; виділяються лінійні ділянки побудованих кривих; проводитися їх апроксимація за методом найменших квадратів; розмірність визначається як тангенс кута нахилу прямої, апроксимуючої графік кореляційного інтеграла C (е).

Кількісну оцінку точності знаходження кореляційної розмірності запропонували Екман і Рюель (1981). Позначимо через еmax – максимальний розмір елементарної комірки, а еmin – її мінімальний розмір, які відповідають початку і кінцю лінійної ділянки залежності С (е) від е в подвійному логарифмічному масштабі. Тоді p = еmax/еmin . Для надійного вимірювання D2 необхідно p=10. Також одна з основних умов даної оцінки полягає у дотриманні нерівності D2<2lgN, де N – довжина часового ряду [8].

Етап № 4. На цьому етапі формується математична модель процесу у вигляді диференціального рівняння і здійснюється прогноз.

Основним математичним апаратом нелінійної динаміки є, як правило, диференціальні рівняння. Саме на їх основі в даній роботі передбачається здійснювати прогноз, а саме, праві частини цих рівнянь описувати за допомогою нейронних мереж [9].

Диференціальні рівняння є основним математичним апаратом нелінійної динаміки, вони застосовуються в якості основного прогностичного інструмента і в даній роботі. Саме, з їх допомогою можна описувати еволюцію системи і прогнозувати її поведінку в наступні моменти часу.

Досвід показує, що штучні нейронні мережі нерідко виявляються більш ефективними, ніж класичні методи прогнозування. Вони дають більш точний результат і дозволяють працювати з зашумленими і неточними даними [3, 10].

Саме тому для прогнозу вибираються звичайні диференціальні рівняння:

dx/dt=f(x,c)

де x – D-мірний вектор стану, , f – вектор - функція, за - Р-мірний вектор параметрів, t – безперервний час.

З використанням програмної системи Fcomplex були проведені експерименти з трьома видами мереж: лінійної, нелінійної та регресійної. Експерименти показали, що найкращий прогноз для дальності прогнозування 1, 3, 6, 9 годин дає нелінійна мережа.

У даному випадку, нелінійна мережа являє собою один прихований шар (від 1 до 10 нейронів) з функцією активації гіперболічного тангенса і вихідним шаром, що містить 1 нейрон з лінійною функцією активації. На рисунку 1 представлена структура нелінійної мережі [11].

Штучна нейронна мережа

Рисунок 1 – Архітектура штучної нейронної мережі (анімація: обсяг – 126,0 КБ; розмір – 500x277; кількість кадрів – 7; нескінченне число циклів повторення; затримка між кадрами – 0,5 с; затримка між останнім і першим кадром – 0,5 с)

Мережа не містить зворотних зв'язків, нейрони з'єднуються за принципом «кожен з кожним». Обидва шари мають зсув. Вага та зміщення настроюються методом Левенберга-Марквардта, критерій якості навчання – середня квадратична помилка [3].

Математичний опис моделі має вигляд:

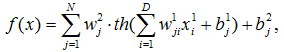
де параметром функції f є часовий ряд x.

Тобто, прогноз передбачається здійснювати за допомогою моделі:

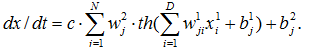
Етап № 5. На цьому етапі відбувається перевірка ефективності моделі. Ефективність моделі визначається її цілями. Оскільки метою моделі є прогноз метеопараметрів, то найкращою перевіркою ефективності буде порівняння отриманих прогнозних значень з істинними значеннями метеопараметрів.

Висновок

Результат магістерської роботи – модель прогнозування метеопараметрів з використанням часових рядів. Дані дослідження і обчислення можуть стати корисними для метеорологів і бути використані для подальших досліджень і удосконалень в цій області.

При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2011 р. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

Література

  1. Гриценко А.В. Реконструкция уравнений и прогнозирование метеопараметров по их временным рядам. [Текст] – Донецк, ДонНТУ, 2010. – 149 с.
  2. Importance of weather forecasting. [Electronic resourse] / Интернет-ресурс. – Режим доступа:http://vasat.icrisat.org/?q=node/300
  3. Климова Е.А., Беловодский В.Н. Дифференциальная математическая модель эволюции метеопараметров. [Текст] – Компьютерный мониторинг и информационные технологии 2011 / Материалы I всеукраинской научно-технической конференции, аспирантов и молодых ученых. – Донецк, ДонНТУ – 2011.
  4. Сивяков А. С. Построение прогностического комплекса и внедрения его в электронную сеть университета. [Текст] – Донецк, ДонНТУ, 2011. – 125 с.
  5. Исследователь. [Electronic resourse] / Интернет-ресурс. – Режим доступа: http://ligis.ru/effects/stat/modules/sttimser.html – Анализ временных рядов.
  6. Чечурин А.В. Исследование алгоритмов оценки размернсоти реконструкции аттракторов [Текст] / Чечурин А.В. // Задачи системного анализа, управления и обработки информации. Межвузовский сборник научных трудов. Вып. 1.— М.: МГУП, 2006. - С.15-23
  7. Гудков Г.В. Диагностические возможности определения детерменированного хаоса в структуре вариабельности ритма сердца плода [Electronic resourse] / Интернет-ресурс. – Режим доступа:http://vestnik.kmldo.ru/pdf/08/01/02.pdf
  8. Антипов О.И., Неганов В.А. Фрактальный анализ нелинейных систем и построение на его основе прогнозирующих нейронных сетей [Текст] / О. И. Антипов, В. А. Неганов // Физика волновых процессов и радиотехнические системы. - 2010. - Т. 13, N 3. - С. 54-63
  9. Козлов Д.А. Методы нелинейной динамики в моделировании макро-экономических процессов [Electronic resourse] / Интернет-ресурс. – Режим доступа: http://www.ecfor.ru/pdf.php?id=books/kor001/09
  10. Безручко, Б.П. Математическое моделирование и хаотические временные ряды [Текст] / Б.П. Безручко, Д.А. Смирнов // Саратов: ГосУНЦ «Колледж», 2005. – С. 320.
  11. Медведев В.С. Нейронные сети. MaTLab 6/ Медведев В.С., Потемкин В.Г. [Под общ. ред. к.т.н. В.Г. Потемкина]. – М.: ДИАЛОГ-МИФИ, 2002. 496 с.