Вступ

    У сучасних умовах оперативна інформація про розташування і пересування рухомих об'єктів, є важливою складовою забезпечення безпеки персонально для кожної людини. Стрімкий розвиток технічних засобів передачі даних, зробили ефективну систему спостереження і контролю за мобільними об'єктами в режимі реального часу. З технічної точки зору створені системи радіо місцевизначення є унікальним науково-технічним комплексом, що забезпечує в даний час найбільшу точність глобальної, тимчасової і координатної прив'язки абонентів. Застосовувані в даний час в цих системах радіосигнали забезпечують необхідний рівень граничної точності проведення вимірювань координат рухомого об'єкта.

Актуальність теми

    Дана задача є актуальною, тому що вибір ефективного алгоритму для визначення координат рухомого об'єкта, це головна складова в розробці модуля відображення системи логістики.

Наукова значущість роботи

    Наукова цінність даної роботи полягає в аналізі алгоритмів визначення координат, а так само можливості модифікації їх для використання в системах логістики.

Практична цінність результатів роботи

    У ході виконання роботи за результатами експериментальних досліджень визначено самий ефективний алгоритм визначення координат рухомого об'єкта.

Огляд досліджень по темі у ДонНТУ

    Подібні питання досліджувалися:

1. Магістр ФКНТ Паршин А. Н. по темі: "Обчислення координат рухомого об'єкта"
2. Магістр ФКНТ Порицький А. В. по темі: "Алгоритми генерації траєкторії руху рухомого об'єкта"

Огляд досліджень по темі у Україна

    В Україні дослідженням даного питання займалися:

1. Бондарук А.Б., Глухов В.С., Євтушенко К.С., Оліярник Б.О. Львівський науково-дослідний радіотехнічний інститут, *Національний університет “Львівська політехніка” тема: "ГАРАНТОЗДАТНА ІНТЕГРОВАНА СИСТЕМА НАВІГАЦІЇ РУХОМИХ НАЗЕМНИХ ОБ’ЄКТІВ"
2. Овсяникова Т. В.*, Бушанская В. В.*, Игдалов И. М.**, Фролов В. П.*, Попель В. М.* Государственное предприятие "Конструкторское бюро "Южное" им. М.К. Янгеля * Днепропетровский национальный университет ** тема: "ОПРЕДЕЛЕНИЕ КООРДИНАТ МЕСТОПОЛОЖЕНИЯ НАЗЕМНОГО ПОДВИЖНОГО ОБЪЕКТА" кафедра електронних обчислювальних машин

Огляд досліджень по темі у світі

    У світі дослідженням даного питання займалися:

1. Elliott Kaplan, Christopher Hegarty за темою: "Understanding GPS: Principles and Applications"

Основні результати

    Супутникові системи навігації

    Супутникова система навігації - комплексна електронно-технічна система, що складається із сукупності наземного і космічного устаткування, призначена для визначення місця розташування (географічних координат і висоти), а також параметрів руху (швидкості та напрямку руху) для наземних, водних і повітряних об'єктів.
   Основные элементы спутниковой системы навигации:

• Орбітальна угрупування, що складається з декількох (від 2 до 30) супутників, випромінюючих спеціальні радіосигнали;
• Наземна система управління та контролю, що включає блоки вимірювання поточного положення супутників і передачі на них отриманої інформації для коректування інформації про орбіти;
• Приймальне клієнтське обладнання ("супутникових навігаторів"), що використовується для визначення координат;
• Опціонально: інформаційна радіосистема для передачі користувачам поправок, що дозволяють значно підвищити точність визначення координат.

   Принцип роботи супутникових систем навігації заснований на вимірюванні відстані від антени на об'єкті (координати якого необхідно отримати) до супутників, положення яких відомо з великою точністю. Таблиця положень всіх супутників називається альманахом, яким повинен володіти будь супутниковий приймач до початку вимірювань. Звичайно приймач зберігає альманах у пам'яті з часу останнього виключення і якщо він не застарів - миттєво використовує його. Кожен супутник передає у своєму сигналі весь альманах. Таким чином, знаючи відстані до декількох супутників системи, за допомогою звичайних геометричних побудов, на основі альманаху, можна обчислити положення об'єкта в просторі. Метод вимірювання відстані від супутника до антени приймача заснований на визначеності швидкості поширення радіохвиль. Для здійснення можливості вимірювання часу поширення радіосигналу кожен супутник навігаційної системи випромінює сигнали точного часу в складі свого сигналу використовуючи точно синхронізовані з системним часом атомний годинник. При роботі супутникового приймача його годинник сінхронізувався з системним часом і при подальшому прийомі сигналів обчислюється затримка між часом випромінювання, що містяться в самому сигналі, і часом прийому сигналу. Маючи в своєму розпорядженні цією інформацією, навігаційний приймач обчислює координати антени. Додатково накопичуючи та обробляючи ці дані за певний проміжок часу, стає можливим обчислити такі параметри руху, як швидкість (поточну, максимальну, середню), пройдений шлях і т.д.

   Виды спутниковых систем

   В даний час працюють або готуються до розгортання наступні системи супутникової навігації:
NAVSTAR (GPS)
   Більш відома під назвою GPS. Державне підприємство Міністерства оборони США. Єдина повнофункціональна супутникова навігаційна система.
ГЛОНАСС
   Державне підприємство Міністерства оборони Росії. Знаходиться на етапі повторного розгортання супутникового угруповання (оптимальний стан орбітального угрупування супутників, запущених в СРСР, було в 1993-1995 рр..). Використовується як допоміжна система, що поліпшує результати GPS позиціонування в областях з закритими ділянками неба (в умовах щільної міської забудови) і в приполярних широтах.
GALILEO
   Європейська система, що знаходиться на етапі створення супутникового угруповання.
BEIDOU (COMPASS)
   Розгортається в даний час Китаєм підсистема GNSS, призначена для використання тільки в цій країні. Особливість - невелика кількість супутників, що знаходяться на геостаціонарній орбіті.
IRNSS
   Індійська навігаційна супутникова система, в стані розробки.



Рисунок 1. ГЛОНАСС

   Алгоритми прийому та вимірювання параметрів супутникових радіонавігаційних сигналів

До сегмента споживачів систем GPS і ГЛОНАСС відносяться приймачі сигналів супутників. За вимірами параметрів цих сигналів вирішується навігаційна завдання.
Приймач можна розділити на три функціональні частини:

радіочастотну частина;
цифровий ~ корелятор;
процесор.

   З виходу антенно-фідерного пристрою (антени) сигнал надходить на радіочастотну частина (рис. 1). Основне завдання цієї частини полягає в посиленні вхідного сигналу, фільтрації, перетворенні частоти і аналого-цифровому перетворенні. Крім цього, з радіочастотної частини приймача надходить тактова частота для цифрової частини приймача. З виходу радіочастотної частини цифрові відліки вхідного сигналу надходять на вхід цифрового коррелятора.


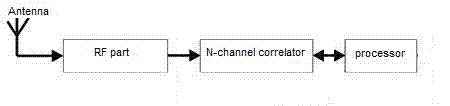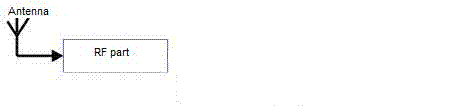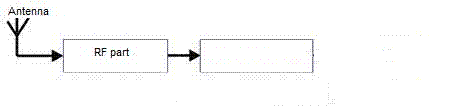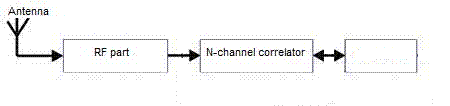
Рисунок 2. Узагальнена структура приймача

   У корелятори спектр сигналу переноситься на "нульову" частоту. Це проводиться шляхом перемноження вхідного сигналу коррелятора з опорним гармонійним коливанням в синфазном і квадратурної каналах. Далі результат перемноження проходить кореляційну обробку шляхом перемноження з опорним далекомірним кодом і накопиченням на періоді далекомірного коду. У підсумку отримуємо кореляційні інтеграли I і Q. Відліки кореляційних інтегралів надходять у процесор для подальшої обробки і замикання петель ФАП (фазова автопідстроювання) і ССЗ (схема стеження за затримкою). Вимірювання параметрів сигналу в приймачі виробляються не безпосередньо по вхідному сигналу, а за його точної копії, що формується системами ФАП і ССЗ. Кореляційні інтеграли I і Q дозволяють оцінити ступінь "схожості" (корельованості) опорного і вхідного сигналів. Завдання коррелятора, крім формування інтегралів I і Q, - формувати опорний сигнал, згідно з керуючими впливами (кодами управління), які надходять з процесора. Крім того, в деяких приймачах корелятор формує необхідні вимірювання опорних сигналів і передає їх у процесор для подальшої обробки. У той же час, так як опорні сигнали в корелятори формуються по керуючим кодами, що надходять з процесора, то необхідні вимірювання опорних сигналів можна проводити безпосередньо в процесорі, обробляючи відповідним чином керуючі коди, що і робиться в багатьох сучасних приймачах. Дальність при радіотехнічних вимірах характеризується часом поширення сигналу від об'єкта вимірювання до вимірювального пункту. У навігаційних системах GPS / ГЛОНАСС випромінювання сигналів синхронізовано зі шкалою часу системи, точніше, зі шкалою часу супутника, що випромінює даний сигнал.
   У той же час, споживач має інформацію про розбіжність шкали часу супутника і системи. Цифрова інформація, передана з супутника, дозволяє встановити момент випромінювання деякого фрагмента сигналу (мітки часу) супутником у системному часу. Момент прийому цього фрагмента визначається за шкалою часу приймача. Шкала часу приймача (споживача) формується за допомогою кварцових стандартів частоти, тому спостерігається постійний "догляд" шкали часу приймача щодо шкали часу системи. Різниця між моментом прийому фрагмента сигналу, відрахувати по шкалі часу приймача, і моментом випромінювання його супутником, відрахувати по шкалі супутника, помножена на швидкість світла, називається псевдодальністю.

   Алгоритми адаптивної фільтрації

   При пошуку оптимальних алгоритмів обробки сигналу неминуче доводиться спиратися на деякі статистичні моделі сигналів і шумів. Найчастіше при формуванні цих моделей використовуються концепції лінійності, стаціонарності і нормальності. Однак перераховані принципи далеко не завжди виконуються на практиці, а від адекватності обраної моделі значною мірою залежить якість прийому сигналу. Можливим рішенням проблеми є використання адаптивних фільтрів, які дозволяють системі підлаштовуватися під статистичні параметри вхідного сигналу, не вимагаючи при цьому завдання будь-яких моделей.

   Алгоритм LMS

   Один з найбільш поширених адаптивних алгоритмів заснований на пошуку мінімуму цільової функції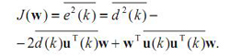
методом найшвидшого спуску. При використанні даного способу оптимізації вектор коефіцієнтів фільтра w (k) повинен рекурсивно оновлюватися наступним чином:
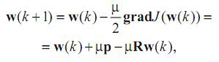    (1)
де µ - позитивний коефіцієнт, званий розміром кроку.
   Проте для розрахунку градієнта необхідно знати значення матриці R і вектора p. На практиці можуть бути доступні лише оцінки цих значень, одержувані за вхідними даними. Найпростішими такими оцінками є миттєві значення кореляційної матриці і вектора взаємних кореляцій, що виробляються без будь-якого усереднення:

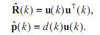
    При використанні даних оцінок формула (1) приймає наступний вигляд:

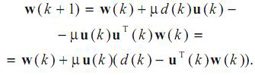
   Вираз, що стоїть у дужках, згідно 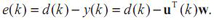, являє собою різницю між зразковим сигналом і вихідним сигналом фільтра на k - му кроці, тобто помилку фільтрації e (k). З урахуванням цього вираз для рекурсивного оновлення коефіцієнтів фільтра виявляється дуже простим: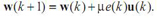
   (2)
   Алгоритм адаптивної фільтрації, заснований на формулі (2), отримав назву LMS (Least Mean Square, метод найменших квадратів). Існує велика кількість модифікацій алгоритму LMS, спрямованих на прискорення збіжності або на зменшення числа арифметичних операцій. Прискорення збіжності може бути досягнуто за рахунок поліпшення використовуваної оцінки градієнта, а також за рахунок перетворення вхідного сигналу з метою зробити його відліки некоррелірованнимі. Зменшення обчислювальної Складність може бути досягнуте, зокрема, за рахунок використання в (2) не самих сигналу помилки і вмісту лінії затримки фільтра, а лише їх знаків. Це дозволяє повністю позбутися від операцій множення при оновленні коефіцієнтів філь? тра. В цілому слід зазначити, що вимоги прискорення збіжності та скорочення обчислювальних витрат є суперечливими.

   Алгоритм RLS

   У принципі, в процесі прийому сигналу можна на кожному черговому кроці перераховувати коефіцієнти фільтра безпосередньо за формулою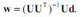 , проте це пов'язано з невиправдано великими обчислювальними витратами. Дійсно, розмір матриці U постійно збільшується і, крім того, необхідно кожен раз заново обчислювати зворотну матрицю. Скоротити обчислювальні витрати можна, якщо зауважити, що на кожному кроці до матриці U додається лише один новий стовпець, а до вектора d - один новий елемент. Це дає можливість організувати обчислення рекурсивно. Відповідний алгоритм називається рекурсивним методом найменших квадратів (Recursive Least Square, RLS).
    При використанні алгоритму RLS виробляється рекурсивне оновлення оцінки зворотного кореляційної матриці, а висновок формул грунтується на наступному матричному тотожність:
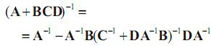   (3)
   де A і C - квадратні невироджені матриці (необов'язково однакових розмірів), а B і D - матриці сумісних розмірів.
Застосування формули (3) для рекурсивного оновлення зворотної кореляційної матриці P в поєднанні з вихідною формулою 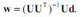для коефіцієнтів оптимального фільтру дає наступну послідовність кроків адаптивного алгоритму RLS.

1. При надходженні нових вхідних даних u (k) виробляється фільтрація сигналу з використанням поточних коефіцієнтів фільтра w (k - 1) та обчислення величини помилки відтворення зразкового сигналу:
   
2. Розраховується вектор - стовпець коефіцієнтів посилення (слід зазначити, що знаменник дробу в наступних двох формулах є скаляром, а не матрицею):
   
3. Проводиться оновлення оцінки зворотного кореляційної матриці сигналу:
   
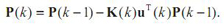
4. Нарешті, проводиться оновлення коефіцієнтів фільтра:
   

   Головним достоїнством алгоритму RLS є швидка збіжність. Однак досягається це за рахунок значно більш високої (у порівнянні з алгоритмом LMS) обчислювальної складності .

   Алгоритм Калмана

   Мета фільтра Калмана - мінімізувати дисперсію оцінки векторного випадкового процесу x (k), що змінюється в часі таким чином: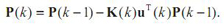
    де Ф (k) - матриця переходу, v (k) - випадковий вектор
    При використанні фільтра Калмана для рішення задачі адаптивної фільтрації відстежує процеси є вектор коефіцієнтів оптимального фільтра w. Передбачається, що детермінованих змін коефіцієнтів не відбувається, тому матриця переходу Ф є одиничною: Ф (k) = I. В якості матриці спостереження виступає вектор вмісту лінії затримки фільтра u (k). Таким чином, вихідний сигнал фільтра представляє собою прогнозоване значення спостережуваного сигналу, а в якості самого спостережуваного сигналу виступає зразковий сигнал адаптивного фільтра d (k). Шум спостереження в даному випадку є помилкою відтворення зразкового сигналу, а матриця перетворюється на скалярний параметр- середній квадрат сигналу помилки. Як наголошується раніше, величина цього параметра слабко впливає на поведінку алгоритму.
   Якщо фільтрується стаціонарний випадковий процес, коефіцієнти оптимального фільтру є постійними і можна прийняти Q = 0. Щоб дати фільтру можливість відстежувати повільні зміни статистики вхідного сигналу, в якості Q може використовуватися діагональна матриця.
   У результаті наведені вище формули приймають такий вигляд:

1.    — вихідний сигнал фільтра (прогнозоване значення зразкового сигналу);
2.    — помилка фільтрації;
3.    — калмановського коефіцієнт посилення;
4.    — оновлення оцінки коефіцієнтів фільтра w (k);
5.    — оновлення оцінки кореляційної матриці помилок оцінювання.

   Початкове значення вектора w звичайно приймається нульовим, а в як вихідної оцінки матриці P використовується діагональна матриця виду CI.
   Порівнюючи формули, що описують алгоритми RLS і Калмана, легко помітити їх схожість. Обчислювальна складність і якісні параметри двох алгоритмів також виявляються досить близькими. Різниця полягає лише у вихідних посилках, що використовувалися при виведенні формул, і в трактуванні параметрів алгоритмів. У деяких джерелах алгоритми RLS і Калмана стосовно до адаптивної фільтрації ототожнюються.

   Висновок

   На даний момент був проведений аналіз алгоритмів визначення координат і виконано модифікацію алгоритму для використання в системах логістики. При написанні автореферату магістерська робота знаходилася в процесі розробки. Остаточне завершення листопад 2011 року.

   Література

1. Радиотехнические системы. Под ред. Казаринова Ю.М. М.: Высшая школа, 1990.
2. Соловьев Ю.А. Системы спутниковой навигации. М.: Эко-Трендз, 2000.
3. Глобальная спутниковая радионавигационная система ГЛОНАСС / Под ред. В.Н. Харисова, А.И. Перова, В.А. Болдина. М.: ИПРЖР, 1998.
4. Липкин И.А. Спутниковые навигационные системы. М.: Вузовская книга, 2001.
5. images.nature.web.ru/nature/2003/04/11/0001193683/06.pdf
6. Глобальная навигационная спутниковая система ГЛОНАСС. Интерфейсный контрольный документ. М.: КНИЦ ВКС, 1995.
7. Interface Control Document: NAVSTAR GPS Space Segment / Navigation User Interfaces (ICD-GPS-200). Rockwell Int. Corp. 1987.
8. Уидроу Б., Стирнз С. Д. Адаптивная обработка сигналов.— М.: Радио и связь, 1989.— 440 с
9. Адаптивные фильтры: Пер. с англ. / Под ред. К.Ф.Н. Коуэна и П.М. Гранта.— М.: Мир, 1988.—392 с.
10. Glentis G.O., Berberidis K., Theodoridis S. Efficient Least Squares Adaptive Algorithms for FIR Transversal Filtering // IEEE Signal Processing Magazine.— 1999.— V. 16.—N. 4.—P. 13–41
11. Haykin S. Adaptive Filter Theory, 4th edition.— Prentice Hall, 2002.— 936 p.
12. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д. Д. Кловского.— М.: Радио и связь, 2000.—800 с