Реферат на тему: Исследование и разработка специализированных программных способов для моделирования автоколебаний
Содержание
Введение
Актуальность работы
Цели и предполагаемая научная новизна
Планируемые практические результаты
1. Архитектура моделирующих программ
1.1 Модульная структура программ математического моделирования динамических систем
1.2 Архитектура математического ядра моделирующих программ с поточной моделью управления
1.3 Графический интерфейс программ математического моделирования динамических систем
2. Моделирование систем уравнений в среде MATLAB
Заключение
Список использованной литературы
Введение
Известно много хороших математических программ. Отнесем каждую к одной из двух групп:
- Мощные калькуляторы для статических вычислений (Matcad, Mathematica, Maple).
- Специализированные решатели для моделирования динамических процессов (DyMoLa, Dynast, Multisim, VisSim, MBTY, MVS, Simulink).
При использовании программ и той, и другой группы пользователю нужно определить последовательность математических функций, которые должны быть вычислены математическими ядрами. Фундаментальное отличие проявляется в том, что при использовании программ-калькуляторов пользователь должен рассчитывать лишь на однократное вычисление запрограммированной им последовательности функций, а при использовании динамических решателей может использовать возможности повторных вычислений. Таким образом, с одной стороны, если в вашем распоряжении программа-калькулятор, то вам нужно знать громадное количество методов, позволяющих сократить количество математических операций [1] (что спасет вас от мозоля на пальце). А с другой стороны, нельзя поспорить с тем, что при использовании динамических решателей для решений задач «в лоб» (т.е. в четком соответствии с их физической природой, без использования накрученных на физическую природу математических абстракций второго, третьего порядка или жестко формализованных (матричных) подходов), придется серьезно загрузить «бедный» процессор компьютера несколькими миллиардами математических операций на две или даже десять секунд.
Компьютеры, безусловно, изобретались не для офисных приложений. Мозг же студента развивается не существенно от запоминания большого количества формализованных или жёстко алгоритмизированных методик, которые разрабатывались еще до появления компьютеров в целях уменьшения количества вычислений. Эти факты объясняют существенный интерес ведущих педагогов к программам математического моделирования динамических систем. Однако ограничения в доступности подобных программ, стремление производителей скрыть технологии их функционирования, плюс всенародная любовь к «калькуляторам» сдерживают их широкое распространение, порождают недоверие к ним, что, в конечном счете, сказывается на их качестве.
Актуальность работы
Расширение круга научно-технических задач встающих перед вычислительной техникой требует создания высокоэффективных средств в моделировании. Использование средств распараллеливания приводит к постановлению задач обоснованного синтеза вычислительных процессов с минимальными накладными расходами при реализации на штатных ОС. В этой связи задача проектирования оптимального расписания при моделировании жестких динамических систем представляется актуальной.
Цели и предполагаемая научная новизна
Повышение цифровой части комплекса при решении задач моделирования жёстких динамических систем и расширение класса решаемых задач.
Планируемые практические результаты
1. Анализ методов планирования вычислительных процессов реального времени в современных операционных системах;
2. Разработка алгоритма планировщика без прерываний вычислительного процесса методами теории расписания;
3. Программная реализация тестовой модели автоколебаний на основе разработанного специализированного программного обеспечения.
1. Архитектура моделирующих программ
1.1 Модульная структура программ математического моделирования динамических систем
Сколь разными бы ни казались моделирующие программы, их модульная структура практически неизменна (см. рис. 1):
- Графический интерфейс ориентирован на человека и отвечает за представление математической модели в виде, понятном широкому кругу специалистов. Это могут быть блок-схемы, схемы физические принципиальные, гибридные карты состояний и пр.
- Система управления базой данных отвечает за хранение объектов составленной пользователем модели и требуемые трансформации структуры ее хранилища.
- Математическое ядро берет на себя основную вычислительную нагрузку, и, в цикле, согласно заданной программе, руководствуясь готовностью аргументов, а в редких спорных случаях (появление которых всегда можно избежать) приоритетностью математических операций, обеспечивает исполнение потоков математических функций.
- Серверы визуализации и Online воздействий обеспечивают интерфейс между функционирующим математическим ядром и пользователем. Серверы визуализации результатов — осциллографирующие, показывающие, и индицирующие приборы — в зависимости от ситуационных требований, могут работать либо в синхронном, либо в асинхронном режиме. Серверы же Online воздействий на модель жестко синхронизированы с математическим ядром.

|
Рисунок 1 – Модульная структура моделирующих программ
|
К большому сожалению, разработчики моделирующих программ при создании своих продуктов не придерживаются современных технологий модуляризации (COM, CORBA) и предпочитают все делать самостоятельно. Их консерватизм в этом отношении создает потенциально неустойчивую ситуацию на рынке. Все представленные на рис. 1 модули могут быть не просто автономными, а уже традиционно считаются независимыми программными продуктами. Математическое ядро — это наиболее простой и легкий в создании модуль. Совершенно очевидно, что создание полноценного редактора векторной графики подобного Visio или CorelDraw или же движка реляционной базы данных — это задача не для фирмы со штатом из 3..10 человек. Именно усилия, потраченные на решение этих второстепенных задач, разорили далеко не одну компанию, а проигрывают от этого пользователи.
За последние десять лет ситуация изменилась не в пользу описанной позиции разработчиков моделирующих программ. Вспомогательные модули созданы конкурирующими между собой сторонними производителями, широко доступны, обеспечивают требуемые механизмы интеграции с другими программными комплексами и непрерывно совершенствуются профессионалами в своей области.
1.2 Архитектура математического ядра моделирующих программ с поточной моделью управления
Какими бы разными ни были моделирующие программы, вариации архитектуры их математических ядер довольно жестко ограничены возможностями компиляторов языков высокого уровня. Очевидно, что математическое ядро должно поддерживать от 100 до нескольких тысяч математических функций. Безусловно, требуется формализация интерфейса настройки и управления математического ядра, поскольку справиться с таким громадным количеством функций, используя их ручной вызов, невозможно.
1.3 Графический интерфейс программ математического моделирования динамических систем
Графический интерфейс — это самое 'слабое место' программ математического моделирования динамических систем. Попробуем разобраться с тем, что может понимать русскоязычный специалист под скромным английским термином диаграмма (diagram), если с помощью неё требуется представить описание модели системы на том или ином уровне в графической форме:
1. Блок-схемы или около десятка именованных направленных графов.
2. Схемы физические принципиальные электрических, магнитных, тепловых, гидравлических, акустических, механических, ротационных, и др. цепей преобразования энергий. Они же ненаправленные или би(со)направленные графы.
3. Гибридные карты состояния или импульсные потоковые графы, графы переходных состояний.
4. Графы алгоритмов программ.
5. Структурные схемы, функциональные схемы, мнемосхемы.
6. И многое другое.
Разнообразие впечатляет. Однако цель перечисления не в потрясении воображения читателя, а в том, чтобы подвести к мысли о том, что задача создания графического интерфейса непроста и не соответствует квалификации разработчиков моделирующих программ. Конечный пользователь должен понимать, что без кооперации усилий нескольких фирм эту задачу не решить (спрос пользователя рождает предложение). С задачей качественного отображения всего перечисленного, в любых масштабах, на любых устройствах ввода вывода, могут справиться лишь редакторы векторной графики — это их прямая задача. Дополнительным требованием к претенденту на её выполнение является открытость объектной архитектуры и наличие документации.
Как бы ни было велико разнообразие способов графического описания моделей, четко просматриваются лишь две техники моделирования: структурное моделирование и мультидоменное физическое моделирование. Для поддержки структурного моделирования требуется решатель систем дифференциальных уравнений и блок-схемы[2]. Для поддержки мультидоменного физического моделирования требуется итерационный решатель систем алгебро-дифференциальных уравнений и схемы физические принципиальные[3]. Другие виды графов либо мало эффективны, либо являются предками направленных и ненаправленных графов соответственно. Моделирование же управляемое событиями не является новой техникой моделирования, а лишь дополняет названные совокупностью методов переключения и синхронизации фрагментов моделей в процессе симуляции, обеспечивая тем самым программный контроль над потоком.
2. Моделирование систем уравнений в среде MATLAB
Для простоты моделирования систем уравнений берем среду MATLAB. Моделировать будем систему, состоящую из 3х уравнений, из которых 2 представляют уравнение Ван дер Поля, 3е выражает зависимости между  и
и  . Система имеет вид:
. Система имеет вид:

Для решения данной системы были созданы 2 файла:
- vdpol.m будет содержать функцию, для вычисления системы
function xdot = vdpol(t, x)
w=[1 1];
T=1-x(1)^2-x(3)^2;
xdot = [x(2);...
-w(1)^2*(x(1));...
x(4);...
-w(2)^2*(x(3)+T)];
end
- vdpol_LANCH.m будет содержать команды для вызова функции vdpol.
t0=[0 10]; %Интервал моделирования
x0 = [0 0.3 0 0.7]; %Начальные условия
[t, X] = ode45('vdpol', t0, x0);
[m,n] = size(X)
plot(t, X)
figure; surfc([1:n], [1:m], X)
shading interp
colorbar
Для проведения исследований используем следующие начальные значения:

Проведем несколько замеров с различными значениями  .
.
1. 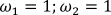 .
.
После выполнения функции получим следующий временной график и трехмерная модель.

|
Рисунок 20 – Временной график при 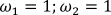
|
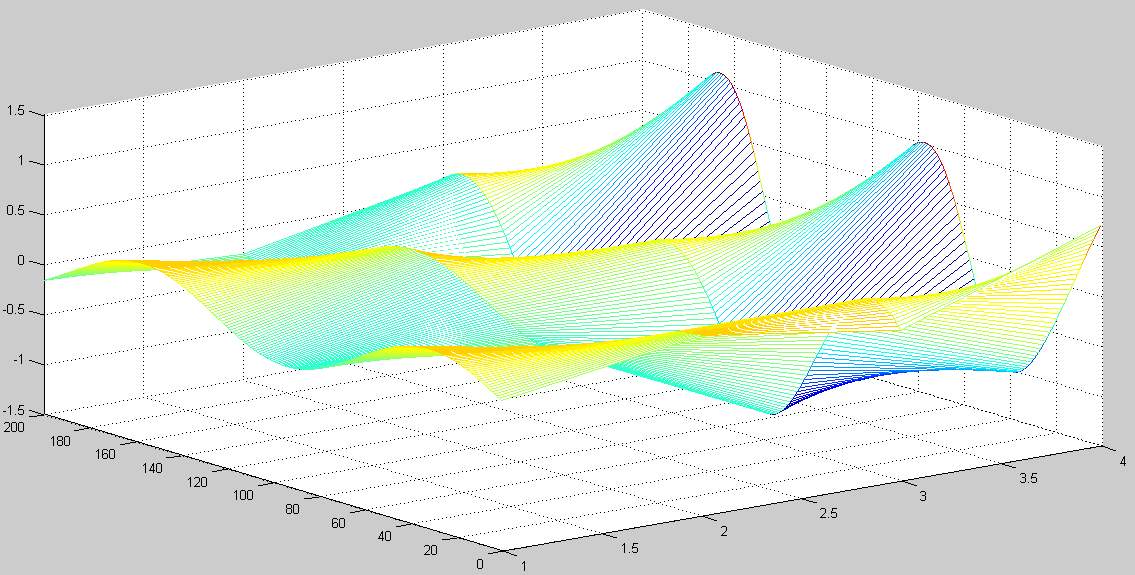
|
Рисунок 21 – Трехмерная модель при 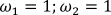
|
2. 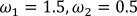 .
.
После выполнения функции получим следующий временной график и трехмерная модель.

|
Рисунок 22 – Временной график при 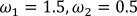
|

|
Рисунок 23 – Трехмерная модель при 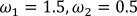
|
3. 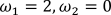 .
.
После выполнения функции получим следующий временной график и трехмерная модель.

|
Рисунок 24 – Временной график при 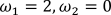
|

|
Рисунок 25 – Трехмерная модель при 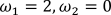
|
4. 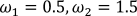 .
.
После выполнения функции получим следующий временной график и трехмерная модель.

|
Рисунок 26 – Временной график при 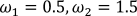
|

|
Рисунок 27 – Трехмерная модель при 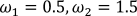
|
Заключение
В данной работе в среде MATLAB была промоделирована система уравнений Ван дер Поля состоящая из трех уравнений с двумя неизвестными. В ходе моделирования использовались различные входные данные. Все промоделированные системы уравнений имеют временные графики. Так же для систем уравнения представлены их трехмерные модели.
При написании данного реферата магистерская работа еще не завершена.
Список использованной литературы
1. Клиначёв Н. В. Обзор архитектурного построения программ математического моделирования динамических систем. - Челябинск, 2004.[электронный ресурс]. – Режим доступа: www/URL:http://model.exponenta.ru/simkernel.html
2. Клиначёв Н. В. О структурном кризисе в методике преподавания блока дисциплин связанных с расчетом цепей преобразования энергий. - Челябинск, 2003.[электронный ресурс]. – Режим доступа: www/URL:http://model.exponenta.ru/lectures/sml_06.htm
3. Клиначёв Н. В. Введение в технологию моделирования на основе направленных графов. - Челябинск, 2003.[электронный ресурс]. – Режим доступа: www/URL:http://model.exponenta.ru/lectures/sml_02.htm
4. Клиначёв Н. В. Введение в технологию мультидоменного физического моделирования с применением ненаправленных графов. - Челябинск, 2003.[электронный ресурс]. – Режим доступа: www/URL:http://model.exponenta.ru/lectures/sml_03.htm
5. Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990. 512 с.
6. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999. 685 с.
7. Козлов О.С., Медведев В.С. Цифровое моделирование следящих приводов. В кн.: Следящие приводы. В 3-х т. Под ред. Б.К. Чемоданова. М.: Изд. МГТУ им. Н.Э. Баумана, т. 1, 1999, с.711-806.
8. Shampine L.F., Reichelt M.W. The MATLAB ODE Suite // SIAM J. on Scientific Computing. Vol. 18. 1997. № 1. P. 1-22.
9. Bogacki P., Shampine L.F. A 3(2) pair of Runge-Kutta formulas // Applied Mathematics Letters. Vol. 2. 1989. № 4. P. 321-325.
10. Hosea M.E., Shampine L.F. Analysis and implementation of TRBDF2 // Applied Numerical Mathematics. Vol. 20. 1996. № 1-3. P. 21-37.
11. Скворцов Л. М. Адаптивные методы численного интегрирования в задачах моделирования динамических систем // Изв. РАН. Теория и системы управления. 1999. № 4. С. 72-78.
12. Скворцов Л. М. Явные адаптивные методы численного решения жестких систем // Математическое моделирование. Т. 12. 2000. № 2. С. 97-107.
13. Скворцов Л. М. Диагонально неявные FSAL-методы Рунге-Кутты для жестких и дифференциально-алгебраических систем // Математическое моделирование. Т. 14. 2002. № 2. С. 3-17.







