Реферат на тему: Дослідження та розробка спеціалізованих програмних засобів для моделювання автоколивань
Зміст
Вступ
Актуальність роботи
Мета роботи і можлива наукова новизна
Плановані практичні результати
1. Архітектура моделюючих програм
1.1 Модульна структура програм математичного моделювання динамічних систем
1.2 Архітектура математичного ядра моделюючих програм з потоковою моделлю управління
1.3 Графічний інтерфейс програм математичного моделювання динамічних систем
2. Моделювання систем рівнянь в середовищі MATLAB
Висновок
Список використаної літератури
Вступ
Відомо багато хороших математичних програм. Віднесемо кожну до однієї з двох груп:
- Потужні калькулятори для статичних обчислень (Matcad, Mathematica, Maple).
- Спеціалізовані вирішувачі для моделювання динамічних процесів (DyMoLa, Dynast, Multisim, VisSim, MBTY, MVS, Simulink).
При використанні програм і тієї, і іншої групи користувачеві потрібно визначити послідовність математичних функцій, які повинні бути обчислені математичними ядрами. Фундаментальна відмінність виявляється в тому, що при використанні програм-калькуляторів користувач повинен розраховувати лише на одноразове обчислення запрограмованої їм послідовності функцій, а при використанні динамічних вирішувачів може використовувати можливості повторних обчислень. Таким чином, з одного боку, якщо у вашому розпорядженні програма-калькулятор, то вам потрібно знати величезну кількість методів, що дозволяють скоротити кількість математичних операцій [1] (що врятує вас від мозоля на пальці). А з іншого боку, не можна посперечатися з тим, що при використанні динамічних вирішувачів для вирішення задач "в лоб" (тобто в чіткій відповідності з їх фізичною природою, без використання накручених на фізичну природу математичних абстракцій другого, третього порядку або жорстко формалізованих (матричних) підходів), доведеться серйозно завантажити "бідний" процесор комп'ютера кількома мільярдами математичних операцій на дві або навіть десять секунд.
Комп'ютери, безумовно, винаходилися не для офісних додатків. Мозок ж студента розвивається не суттєво від запам'ятовування великої кількості формалізованих або жорстко алгоритмізованого методик, які розроблялися ще до появи комп'ютерів з метою зменшення кількості обчислень. Ці факти пояснюють істотне інтерес провідних педагогів до програм математичного моделювання динамічних систем. Проте обмеження в доступності подібних програм, прагнення виробників приховати технології їх функціонування, плюс всенародна любов до "калькуляторів" стримують їх широке розповсюдження, породжують недовіру до них, що, в кінцевому рахунку, позначається на їхній якості.
Актуальність роботи
Розширення кола науково-технічних задач що постають перед обчислювальною технікою вимагає створення високоефективних засобів у моделюванні. Використання засобів розпаралелювання призводить до постанови задач обгрунтованого синтезу обчислювальних процесів з мінімальними накладними витратами при реалізації на штатних ОС. У зв'язку з цим задача проектування оптимального розкладу при моделюванні жорстких динамічних систем представляється актуальною.
Мета роботи і можлива наукова новизна
Підвищення цифрової частини комплексу при вирішенні задач моделювання жорстких динамічних систем і розширення класу вирішуваних задач.
Плановані практичні результати
1. Аналіз методів планування обчислювальних процесів реального часу в сучасних операційних системах;
2. Розробка і дослідження алгоритму планувальника без переривань обчислювального процесу методами теорії розкладу;
3. Програмна реалізація тестової моделі автоколивань на основі розробленого спеціалізованого програмного забезпечення.
1. Архітектура моделюючих програм
1.1 Модульна структура програм математичного моделювання динамічних систем
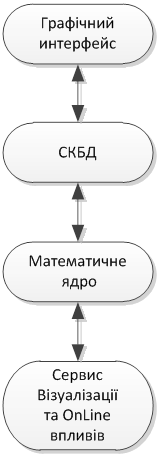
Наскільки різними б не здавалися моделюючі програми, їх модульна структура практично незмінна (див. рис. 1):
- Графічний інтерфейс орієнтований на людину і відповідає за подання математичної моделі у вигляді, зрозумілому широкому колу фахівців. Це можуть бути блок-схеми, схеми фізичні принципові, гібридні карти станів і пр.
- Система управління базою даних відповідає за зберігання об'єктів складеної користувачем моделі і необхідні трансформації структури її сховища.
- Математичне ядро бере на себе основне обчислювальне навантаження, і, в циклі, згідно заданою програмою, керуючись готовністю аргументів, а в окремих спірних випадках (поява яких завжди можна уникнути) пріоритетністю математичних операцій, забезпечує виконання потоків математичних функцій.
- Сервери візуалізації та Online впливів забезпечують інтерфейс між функціонуючим математичним ядром і користувачем. Сервери візуалізації результатів - осціллографуючі, показуючi прилади - залежно від ситуаційних вимог, можуть працювати або в синхронному, або в асинхронному режимі. Сервери ж Online впливів на модель жорстко синхронізовані з математичним ядром.
|
Рисунок 1 - Модульна структура моделюючих програм
|
На превеликий жаль, розробники моделюючих програм при створенні своїх продуктів не дотримуються сучасних технологій модулярізаціі (COM, CORBA) і вважають за краще все робити самостійно. Їх консерватизм у цьому відношенні створює потенційно нестійку ситуацію на ринку. Всі представлені на рис. 1 модулі можуть бути не просто автономними, а вже традиційно вважаються незалежними програмними продуктами. Математичне ядро - це найбільш простий і легкий у створенні модуль. Цілком очевидно, що створення повноцінного редактора векторної графіки подібного Visio або CorelDraw або ж движка реляційної бази даних - це завдання не для фірми зі штатом з 3 .. 10 осіб. Саме зусилля, витрачені на вирішення цих другорядних завдань, понищили далеко не одну компанію, а програють від цього користувачі.
За останні десять років ситуація змінилася не на користь описаної позиції розробників моделюючих програм. Допоміжні модулі створені конкуруючими між собою сторонніми виробниками, широко доступні, забезпечують необхідні механізми інтеграції з іншими програмними комплексами і безперервно вдосконалюються професіоналами у своїй галузі.
1.2 Архітектура математичного ядра моделюючих програм з потоковою моделлю управління
Якими б різними не були моделюючі програми, варіації архітектури їх математичних ядер досить жорстко обмежені можливостями компіляторів мов високого рівня. Очевидно, що математичне ядро має підтримувати від 100 до кількох тисяч математичних функцій. Безумовно, потрібно формалізація інтерфейсу настройки і управління математичного ядра, оскільки справитися з таким величезним кількістю функцій, використовуючи їх ручний виклик, неможливо.
1.3 Графічний інтерфейс програм математичного моделювання динамічних систем
Графічний інтерфейс - це саме "слабке місце" програм математичного моделювання динамічних систем. Спробуємо розібратися з тим, що може розуміти українськомовний фахівець під скромним англійським терміном діаграма (diagram), якщо за допомогою неї потрібно представити опис моделі системи на тому чи іншому рівні в графічній формі:
1. Блок-схеми або близько десятка іменованих направлених графів.
2. Схеми фізичні принципові електричних, магнітних, теплових, гідравлічних, акустичних, механічних, ротаційних, та ін. ланцюгів перетворення енергій. Вони ж неспрямовані або бі(з)спрямовані графи.
3. Гібридні карти стану або імпульсні потокові графи, графи перехідних станів.
4. Графи алгоритмів програм.
5. Структурні схеми, функціональні схеми, мнемосхеми.
6. І багато іншого.
Різноманітність вражає. Проте мета перерахування не в потрясінні уяви читача, а в тому, щоб підвести до думки про те, що завдання створення графічного інтерфейсу непроста і не відповідає кваліфікації розробників моделюючих програм. Кінцевий користувач повинен розуміти, що без кооперації зусиль кількох фірм це завдання не вирішити (попит користувача породжує пропозицію). Із завданням якісного відображення всього перерахованого, в будь-яких масштабах, на будь-яких пристроях вводу виводу, можуть впоратися лише редактори векторної графіки - це їх пряме завдання. Додатковою вимогою до претендента на її виконання є відкритість об'єктної архітектури та наявність документації.
Як би не було велике розмаїття способів графічного опису моделей, чітко проглядаються лише дві техніки моделювання: структурне моделювання і Мультидоменне фізичне моделювання. Для підтримки структурного моделювання потрібні вирішувач систем диференціальних рівнянь і блок-схеми [2]. Для підтримки Мультидоменні фізичного моделювання потрібно ітераційний вирішувач систем алгебро-диференціальних рівнянь і схеми фізичні принципові [3]. Інші види графів або мало ефективні, або є предками спрямованих і неспрямованих графів відповідно. Моделювання ж кероване подіями не є новою технікою моделювання, а лише доповнює названі сукупністю методів перемикання і синхронізації фрагментів моделей у процесі симуляції, забезпечуючи тим самим програмний контроль над потоком.
2. Моделювання систем рівнянь в середовищі MATLAB
Для простоти моделювання систем рівнянь беремо середу MATLAB. Моделювати будемо систему, що складається з 3х рівнянь, з яких 2 представляють рівняння Ван дер Поля, 3є висловлює залежності між  і
і  . Система має вигляд:
. Система має вигляд:

Для вирішення даної системи були створені 2 файли:
- vdpol.m буде містити функцію, для обчислення системи
function xdot = vdpol(t, x)
w=[1 1];
T=1-x(1)^2-x(3)^2;
xdot = [x(2);...
-w(1)^2*(x(1));...
x(4);...
-w(2)^2*(x(3)+T)];
end
- vdpol_LANCH.m буде містити команди для виклику функції vdpol.
t0=[0 10]; %Інтервал моделювання
x0 = [0 0.3 0 0.7]; %Початкові умови
[t, X] = ode45('vdpol', t0, x0);
[m,n] = size(X)
plot(t, X)
figure; surfc([1:n], [1:m], X)
shading interp
colorbar
Для проведення досліджень використовуємо наступні початкові значення:

Проведемо кілька вимірів з різними значеннями  .
.
1. 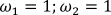 .
.
Після виконання функції отримаємо наступний часовий графік і тривимірна модель.

|
Рисунок 20 – Часовий графік при 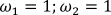
|
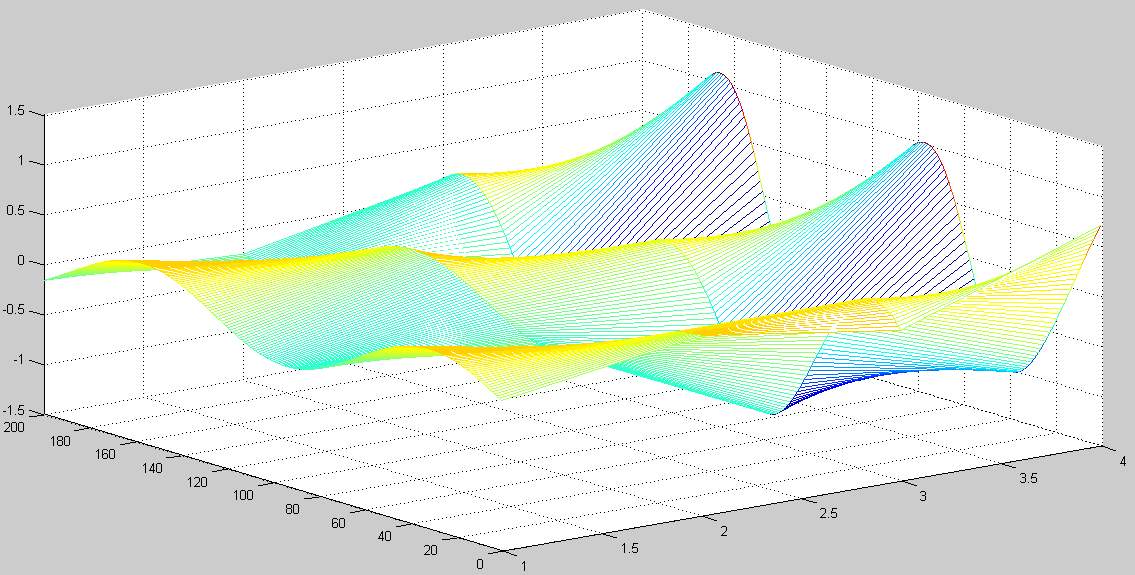
|
Рисунок 21 – Тривимірна модель при 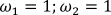
|
2. 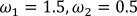 .
.
Після виконання функції отримаємо наступний часовий графік і тривимірна модель.

|
Рисунок 22 – Часовий графік при 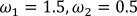
|

|
Рисунок 23 – Тривимірна модель при 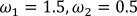
|
3. 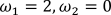 .
.
Після виконання функції отримаємо наступний часовий графік і тривимірна модель.

|
Рисунок 24 – Часовий графік при 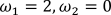
|

|
Рисунок 25 – Тривимірна модель при 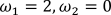
|
4. 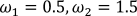 .
.
Після виконання функції отримаємо наступний часовий графік і тривимірна модель.

|
Рисунок 26 – Часовий графік при 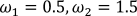
|

|
Рисунок 27 – Тривимірна модель при 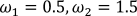
|
Висновок
У даній роботі в середовищі MATLAB була промодельована система рівнянь Ван дер Поля, що складається з трьох рівнянь з двома невідомими. У ході моделювання використовувалися різні вхідні дані. Всі промодельовані системи рівнянь мають тимчасові графіки. Так само для систем рівняння представлені їх тривимірні моделі.
При написанні даного реферату магістерська робота ще не завершена.
Список використаної літератури
1. Клиначёв Н. В. Обзор архитектурного построения программ математического моделирования динамических систем. - Челябинск, 2004.[электронный ресурс]. – Режим доступа: www/URL:http://model.exponenta.ru/simkernel.html
2. Клиначёв Н. В. О структурном кризисе в методике преподавания блока дисциплин связанных с расчетом цепей преобразования энергий. - Челябинск, 2003.[электронный ресурс]. – Режим доступа: www/URL:http://model.exponenta.ru/lectures/sml_06.htm
3. Клиначёв Н. В. Введение в технологию моделирования на основе направленных графов. - Челябинск, 2003.[электронный ресурс]. – Режим доступа: www/URL:http://model.exponenta.ru/lectures/sml_02.htm
4. Клиначёв Н. В. Введение в технологию мультидоменного физического моделирования с применением ненаправленных графов. - Челябинск, 2003.[электронный ресурс]. – Режим доступа: www/URL:http://model.exponenta.ru/lectures/sml_03.htm
5. Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990. 512 с.
6. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999. 685 с.
7. Козлов О.С., Медведев В.С. Цифровое моделирование следящих приводов. В кн.: Следящие приводы. В 3-х т. Под ред. Б.К. Чемоданова. М.: Изд. МГТУ им. Н.Э. Баумана, т. 1, 1999, с.711-806.
8. Shampine L.F., Reichelt M.W. The MATLAB ODE Suite // SIAM J. on Scientific Computing. Vol. 18. 1997. № 1. P. 1-22.
9. Bogacki P., Shampine L.F. A 3(2) pair of Runge-Kutta formulas // Applied Mathematics Letters. Vol. 2. 1989. № 4. P. 321-325.
10. Hosea M.E., Shampine L.F. Analysis and implementation of TRBDF2 // Applied Numerical Mathematics. Vol. 20. 1996. № 1-3. P. 21-37.
11. Скворцов Л. М. Адаптивные методы численного интегрирования в задачах моделирования динамических систем // Изв. РАН. Теория и системы управления. 1999. № 4. С. 72-78.
12. Скворцов Л. М. Явные адаптивные методы численного решения жестких систем // Математическое моделирование. Т. 12. 2000. № 2. С. 97-107.
13. Скворцов Л. М. Диагонально неявные FSAL-методы Рунге-Кутты для жестких и дифференциально-алгебраических систем // Математическое моделирование. Т. 14. 2002. № 2. С. 3-17.







