ДонНТУ   Портал магистров

Реферат

Содержание

Введение

Впервые в мире понятие живучести было сформулировано русским адмиралом Степаном Осиповичем Макаровым – это способность судна продолжать бой, имея повреждения в различных боевых частях [1].

Актуальность темы

Толчком к развитию методов оценки надежности структурно – сложных схем, прогнозирования цепочечных аварий и живучести энергосистем (ЭС) послужила авария, которая случилась 9 ноября 1965 года в США. Эта авария привела к тому, что на территории с населением 30 млн. человек более чем на 10 часов была прекращена жизнедеятельность. Ущерб от аварии составил более 100 млн. долларов [2].

Более 65 % крупных аварий можно отнести к цепочечным, которые происходят в динамическом режиме при коротком замыкании (КЗ) в элементе сети и отказе в срабатывании ряда защитных коммутационных аппаратах, через которые прошел сквозной ток КЗ и привел в действие их релейные защиты [3].

В энергетике под потерей живучести узла нагрузки системы электроснабжения в динамическом режиме будем понимать процесс совпадения в пространстве и времени минимального числа повреждений электрооборудования, при котором происходит аварийное отключение подстанций различных классов напряжения или их секций шин, которые снабжают электроэнергией промышленные предприятия: заводы, фабрики, шахты и т.д.

Под потерей живучести подстанции 110/6 – 10 кВ в динамическом режиме будем понимать процесс совпадения в пространстве и времени минимального числа повреждений электрооборудования, при котором хотя бы одна из секций шин 6 – 10 кВ будет обесточена.

Поэтому работа, направленная на разработку новых и совершенствование известных математических моделей и методик по оценке живучести узлов нагрузки, является актуальной научной задачей, решение которой позволит практически не допускать случаев появление каскадных аварий в энергосистемах, выходу из строя питающих предприятия трансформаторных подстанций в течение заданного времени t.

Цель работы

Получение новой аналитической зависимости вероятности выхода из строя в течение времени t трансформаторной подстанции 110/6 – 10 кВ, которая снабжает электроэнергией промышленные предприятия, в зависимости от параметра потока появления короткого замыкания (КЗ) в отходящих от шин подстанции линий, длительности его существования, надежности систем отключения вводных, фидерных и секционных выключателей и сроков их диагностики.

Научная новизна

На основе регулярных однородных марковских процессов с дискретным числом состояний и непрерывным временем получена математическая модель, которая позволяет оценить живучесть подстанции в динамическом режиме. Получена новая аналитическая зависимость вероятности обесточивания электроснабжения в течении времени t одной из секции шин 6 – 10 кВ подстанции 110/6 – 10 кВ в зависимости от частоты появления КЗ в отходящих от секции шин линий, надежности систем отключения выключателей на подстанции и сроков их диагностики.

Практическая ценность работы

Полученная в работе новая аналитическая зависимость, которая позволяет прогнозировать живучесть узлов и самой подстанции 110/6 – 10 кВ, сравнивать полученный результат с нормируемым уровнем. В том случае, если он будет больше нормируемого 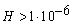1/год ,то представляется возможность выбирать такие сроки диагностики систем отключения выключателей, при которых нормируемый уровень будет обеспечен, т.е. 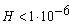1/год.

Основной материал

В энергетике под живучестью объекта понимается свойство противостоять возмущениям, не допуская их каскадного развития с массовым нарушением питания потребителей [4].

Под живучестью узла нагрузки будем понимать способность потребителей и их автоматических средств защиты противостоять возмущениям, которые приводят его к аварийному отключению [5].

В работе [6] предложена общая формула, с помощью которой возможно оценить живучесть конкретной ЭС.

                   (1)

где

Hr – частота появления аварий, которая характеризует живучесть ЭС (либо отдельных ее частей);

λj – параметр потока КЗ, происшедших в j – том элементе;

ωi – параметр потока отказов в срабатывании защитного коммутационного аппарата (ЗКА) через который прошел сквозной аварийный ток при КЗ в j – том элементе сети и привел в действие его токовую защиту;

Θi – интервал времени между диагностиками системы отключения ЗКА, в том числе и токовую защиту;

m – число ЗКА, через которые прошел сквозной аварийный ток и привел в действия их токовые защиты;

r – номер энергосистемы или узла нагрузки;

n – число j – тых элементов КЗ, в которых приводит в действие i – тые ЗКА, через которые прошел сквозной аварийный ток и привел в действие их токовые защиты.

Чем меньше Hr, тем живучесть ЭС выше.

В том случае, если , 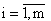формула (1) примет вид:

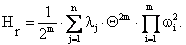              (2)

Формулы (1) и (2) справедливы при выполнении следующих условий:

                                  (3)

– интервалы времени между КЗ и интервалы времени между выявленными отказами в системе отключения ЗКА не противоречат экспоненциальным функциям распределения вероятностей с параметрами и 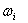соответственно;

– длительность нахождения ЗКА в необнаруженном отказавшем состоянии не противоречит экспоненциальной функции распределения вероятностей;

При выводе формул (1) и (2) были приняты следующие допущения:

– устройства релейной защиты (РЗ) могут выходить из строя только тогда, когда они находятся в режиме ожидания;

– если к моменту возникновения КЗ в сети, на которое должна реагировать РЗ, она находилась в работоспособном состоянии, то маловероятен ее выход из строя в режиме тревоги [7];

– отказы в схеме РЗ или приводе системы отключения ЗКА выявляются и устраняются только в результате абсолютно надежных диагностических проверок, которые происходят с интервалом времени Θi.

Под отказом в срабатывании защитного коммутационного аппарата (ЗКА) будем понимать такой, который приводит к отказу в отключении поврежденного элемента сети при КЗ в зоне действия его релейной защиты [8].

Вероятность выхода из строя r – той ЭС или отдельных ее частей:

                   (4)

если , то .

Узлом нагрузки для трансформаторной подстанции (рис. 1) может быть любая из секций шин – I или II.

Принципиальная схема подстанции 110/6-10 кВ

Рисунок 1 – Принципиальная схема подстанции 110/6 – 10 кВ

Живучесть узла нагрузки определяется в динамическом режиме, то есть, когда в отходящих от секции шин линиях или их потребителях случайно происходят короткие замыкания (КЗ).

Характеризовать живучесть узла нагрузки будем параметром потока его аварийного отключения при КЗ в зоне действия токовой защиты i – го коммутационного аппарата, присоединённого к соответствующей секции шин.

Например, если линия Л1 получает электроэнергию от шины I (рис. 1), то шина I потеряет живучесть при совпадении в пространстве и времени двух случайных событий: – произошло КЗ в линии Л1 и –произошел отказ в срабатывании выключателя под номером i. В этом случае выключатель под номером m+2, который снабжает электроэнергией секцию I, её отключит с помощью токовой защиты и кроме потребителя, который получал электроэнергию от секции I по линии Л1, отключатся и все потребители, которые получали электроэнергию от этой секции шин через соответствующие выключатели (i=2...m).

Если обозначить через Н1 живучесть секции шин I, т.е. параметр потока аварийных отключений секции шин, при КЗ в линиях, потребители которых получают электроэнергию от секции шин I, тогда:

,                    (5)

где

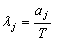,                                                                                        (6)

λj – параметр потока КЗ, происшедших в j – той линии, которая присоединяется к шине I через соответствующий i – тый коммутационный аппарат (j=1...n ), (i=1...m );

aj – число зафиксированных КЗ, которые произошли в j – том отрезке линии за время наблюдения;

Т – время наблюдения за состоянием линий, которые отходят от секции шин I и II и электрооборудованием подстанции.

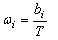,                                                                                        (7)

ωi – параметр потока отказов в срабатывании системы отключения i – того ЗКА (i=1...m );

Θi – интервалы времени между диагностиками системы отключения i – того ЗКА;

bi – число выявленных в результате диагностики повреждений в системе отключения ЗКА, которые могли бы привести к отказу его в срабатывании при КЗ в зоне действия его токовых защит.

Аналогичным образом считается и живучесть Н2 секции шин II. В этом случае λj – будет параметр потока КЗ в линиях, отходящих от соответствующих коммутационных аппаратов, присоединённых к секции II.

Вероятность аварийного отключения секции шин I в течение времени t можно определить следующим образом:

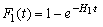,                                                                     (8)

где H1 –живучесть секции I подстанции (параметр потока аварийных отключений секции шин I при КЗ в линиях, потребители которых получают электроэнергию от этой секции шин).

По аналогичной формуле (8) определяется вероятность отключения секции II подстанции, если известна H2.

Пример

Под наблюдением в течение Т=12 лет находилось электрооборудование подстанции 110/6 кВ, которая снабжала электроэнергией одну из шахт Донбасса. От первой системы шин отходили 4 линии и от II также 4. Схема трансформаторной подстанции аналогична схеме (рис. 1).

За это время было зафиксировано следующие короткие замыкания (КЗ), которые произошли в линиях Л1, Л2,…, Л8:

a1=3; a2=4; a3=2; a4=6; a5=5; a6=3; a7=1;a8=0.

Системы отключения ЗКА подстанции проверялись (диагностировались) один раз в год, т.е. Θ=1 год. За время наблюдения 12 лет было выявлено следующее число повреждений, которые могли бы привести к отказу его в срабатывании при КЗ в зоне действия его токовой защиты:

b1=5; b2=4; b3=3; b4=6; b5=0; b6=0; b7=1;b8=7.

Построить дерево событий и схемы минимальных сечений, которое объясняет потерю живучести секции I и II.

Определить:

1) живучесть секции I и II;

2) как изменится живучесть секции шин I и II, если диагностировать систему отключения ЗКА будем через Θ=0,5 года;

3) какова вероятность того, что в течение 10 лет при Θ=1 год секции I и II потеряют живучесть.

Решение. Используя исходные данные примера формулы (6), (7) находим следующие параметры потоков КЗ в линиях и в системе отключения ЗКА:

а) для отходящих от секции шин линий:

λ1=0,25 1/год; λ2=0,33 1/год; λ3=0,17 1/год; λ4=0,5 1/год; λ5=0,42 1/год; λ6=0,25 1/год; λ7=0,08 1/год; λ8=0.

б) для системы отключения ЗКА:

ω1=0,42 1/год; ω2=0,33 1/год; ω3=0,25 1/год; ω4=0,5 1/год; ω5=0; ω6=0; ω7=0,08 1/год; ω8=0,58 1/год;

Анализируя зафиксированные в оперативных журналах результаты наблюдений (Т=12 лет) за появлениями КЗ в отходящих от секции I и II линиях, выявленные и устранённые в ЗКА отказы в системе отключения, которые могли бы привести к отказу их в срабатывании, при случайном появлении КЗ в зоне действия их токовых защит – строим «деревья» и схемы минимальных сечений, которые позволяют объяснить потерю живучести узлов нагрузки (секция I и II) подстанции 110/6 кВ [9].

Обозначим через – событие, произошло КЗ в j-той линии; 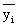– событие, произошёл отказ в системе отключения i-того ЗКА.

Каждое из событий и 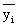характеризуются параметрами потока КЗ – λj и параметром потока отказов в системе отключения ЗКА – ωi.

Дерево событий, которое объясняет потерю живучести секции I и II имеет вид рис. 2 а, в.

Используя рис. 2 а, в строим схемы минимальных сечений рис. 2 б, г.

Пользуясь формулой (1), значениями параметров λj и ωi , полученными с помощью формул (2) и (3) и схемами минимальных сечений рис. 2 б, г находим:

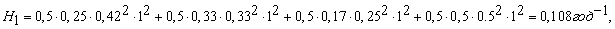
Если же диагностику системы отключения ЗКА проводить через Θ=0,5 года, тогда:

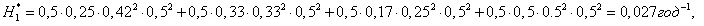
«Дерево» событий и схемы минимальных сечений
«Дерево» событий и схемы минимальных сечений

Рисунок 2 – Дерево событий и схемы минимальных сечений
а) произошло событие – КЗ в линии Лj (j=1...4 ) и 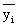– отказал в срабатывании ЗКА (i=1...4 ); б) схема минимальных сечений, составленная для оценки живучести секции I;
в) произошло событие – КЗ в линии Л7, j=7 и событие – отказал в срабатывании ЗКА, i=7; г) схема минимальных сечений, составленная для оценки живучести секции II.

Определим во сколько раз увеличится живучесть секции шин I и II при уменьшении сроков диагностики системы отключения коммутационного аппарата с Θ=1 год на Θ=0,5 года.

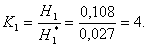
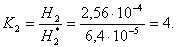
Вероятность того, что в течение t=10 лет при Θ=1 год секции I и II подстанции потеряют живучесть можно оценить с помощью формулы (8):

Выводы

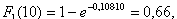
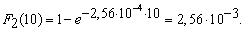
1. Для определения наиболее точной оценки живучести узлов нагрузки подстанции 110/6 – 10 кВ, наблюдение за электрооборудованием следует проводить не за группами однотипных элементов, а конкретно за каждой его единицей. Чем больше время наблюдения за оборудованием подстанции, тем точнее значение живучести узла нагрузки.

2. Наблюдение за работой электрооборудования подстанции следует начинать с момента ее пуска в эксплуатацию до момента утилизации.

3. Наблюдение в течение T=12 лет за электрооборудованием подстанции 110/6 кВ, которая снабжает электроэнергией угольную шахту, установлено, что живучесть секции шин:H1=0,108 1/год, а H2=2,56*10-3 1/год.

4. Показано, что изменение срока диагностики системы отключения ЗКА 6 кВ с Θ=1 год до Θ=0,5 года позволяет увеличить живучесть секции I и II в 4 раза.

5. Определена вероятность того, что в течение t=10 лет секции I и II подстанции потеряют живучесть: F1(10)=0,66, а F2(10)=2,56*10-3.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2012 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список литератyры

  1. Макаров С.О. Разбор элементов, составляющих боевую силу судов.// Морской сборник, 1894,№6, с.1– 106.
  2. Prevention of power failures Vol. 3. Studies of the task groups on the northeast power interruption. A report to the federal power commission. June, 1967, 142 p.
  3. Гук Ю.Б. Теория надежности в электроэнергетике. – Л.: Энергоатомиздат. Ленинградское отд-ние, 1990. – 208 с.
  4. Надежность систем энергетики. Терминология. – М.: Наука, 1980,вып. 95. – 42 с.
  5. Ковалев А.П., Якимишина В.В. О живучести объектов энергетики//Промышленная энергетика, №1, 2006. – с. 20-26.
  6. Ковалев А.П, Якимишина В.В, Нагорный М.А. Оценка надежности узлов нагрузки подстанции 110/10 кВ//Промышленная энергетика, № 11, 2010. – c. 24-28.
  7. Фабрикант В.П. О применении теории надежности к оценке устройств релейной защиты///Электричество, № 9, 1965. – с. 6– 9.
  8. Эндрени Дж. Моделирование при расчётах надёжности в электроэнергетических системах. Пер. с англ./Под ред. Ю.И. Руденко. – М.: Энергоатомиздат, 1983. – 336 с.
  9. Диллон Б., Сингх Ч. Инженерные методы обеспечения надежности систем: Пер. с англ. – М.: Мир, 1984. – 318 с.
  10. Руденко Б.Н., Ушаков И.Н. Надежность систем энергетики. -М.: Наука, 1986. –     252 с.
  11. Китушин В. Г. Определение характеристик отказов системы при цепочечном развитии аварий. – Энергетика и транспорт, 1977, №3.
  12. Ковалев А.П., Чурсинов В. И., Якимишина В. В. Оценка вероятности появления цепочечных аварий в энергосистемах. – Вестник Кременчугского гос.политехн. ун-та, 2004, вып. 3/2004(26).
  13. Горшков В.В. Логико-вероятностный метод расчета живучести сложных систем. – Кибернетика АН УССР.-1982. № 1. – c. 104– 107.
  14. Стекольников Ю.И. Живучесть систем. Теоретические основы.–Санкт-Петербург: Политехника, 2002.– 155 c.
  15. Гук Ю.Б. Теория надежности в электроэнергетике: Учеб. Пособие для вузов. – Л.: Энергоатомиздат, 1990. – 208 с.
  16. Волик Б.Г., Рябинин Й.А. Эффективность, надежность и живучесть управляющих систем // Автоматика и телемеханика. – 1984.– № 12.