Реферат
Зміст
- Вступ
- Актуальність теми
- Мета роботи
- Наукова новизна
- Практична цінність роботи
- Основний матеріал
- Приклад
- Висновки
- Список літератури
Вперше в світі поняття живучості було сформульоване російським адміралом Степаном Осиповічем Макаровим – це здатність судна продовжувати бій, маючи пошкодження в різних бойових частинах [1].
Поштовхом до розвитку методів оцінки надійності структурнo – складних схем, прогнозування цепочечних аварій та живучості енергосистем (ЕС) послужила аварія, яка трапилася 9 листопада 1965 року в США. Ця аварія привела до того, що на території з населенням 30 млн. чоловік більш ніж на 10 годин була припинена життєдіяльність. Збиток від аварії склав більше 100 млн. доларів [2].
Більше 65 % крупних аварій можна віднести до цепочечних, які відбуваються в динамічному режимі при короткому замиканні (КЗ) в елементі мережі й відмові в спрацьовуванні ряду захисних комутаційних апаратів, через які пройшов наскрізний струм КЗ і привів в дію їх релейний захист [3].
У енергетиці під втратою живучості вузла навантаження системи електропостачання в динамічному режимі будемо розуміти процес збігу у просторі та часі мінімального числа пошкоджень електроустаткування, при якому відбувається аварійне відключення підстанцій різних класів напруги або їх секцій шин, які забезпечують електроенергією промислові підприємства: заводи, фабрики, шахти і т.і.
Під втратою живучості підстанції 110/6 – 10 кВ в динамічному режимі будемо розуміти процес збігу у просторі та часі мінімального числа пошкоджень електроустаткування, при якому хоча б одна з секцій шин 6 – 10 кВ буде знеструмлена.
Тому робота, направлена на розробку нових і вдосконалення відомих математичних моделей і методик за оцінкою живучості вузлів навантаження, є актуальною науковою задачею, рішення якої дозволить практично не допускати випадків появи каскадних аварій в енергосистемах, виходу з ладу трансформаторних підстанцій, які живлять підприємства протягом заданого часу t.
Отримання нової аналітичної залежності вірогідності виходу з ладу протягом часу t трансформаторної підстанції 110/6-10 кВ, яка забезпечує електроенергією промислові підприємства, залежно від параметра потоку появи короткого замикання (КЗ) в ліній, що відходять від шин підстанції, тривалості його існування, надійності систем відключення ввідних, фідерних і секційних вимикачів і термінів їх діагностики.
На основі регулярних однорідних марківських процесів з дискретним числом станів і безперервним часом одержана математична модель, яка дозволяє оцінити живучість підстанції в динамічному режимі. Одержана нова аналітична залежність вірогідності знеструмлення електропостачання в перебігу часу t однієї з секції шин 6-10 кВ підстанції 110/6-10 кВ залежно від частоти появи КЗ в лініях, що відходять від секції шин, надійності систем відключення вимикачів на підстанції і термінів їх діагностики.
Одержана в роботі нова аналітична залежність, яка дозволяє прогнозувати живучість вузлів і самої підстанції 110/6 – 10 кВ, порівнювати одержаний результат з нормованим рівнем. В тому випадку, якщо він буде більше нормованого
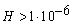 1/год,то представляється можливість вибирати такі терміни діагностики систем відключення вимикачів, при яких нормований рівень буде забезпечений, тобто
1/год,то представляється можливість вибирати такі терміни діагностики систем відключення вимикачів, при яких нормований рівень буде забезпечений, тобто 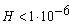 1/год.
1/год.
У енергетиці під живучістю об'єкту розуміється властивість протистояти обуренням, не допускаючи їх каскадного розвитку з масовим порушенням живлення споживачів [4].
Під живучістю вузла навантаження будемо розуміти здатність споживачів і їх автоматичних засобів захисту протистояти обуренням, які приводять його до аварійного відключення [5].
У роботі [6] запропонована загальна формула, за допомогою якої можливо оцінити живучість конкретної ЕС.
 (1)
(1)
де
r – частота появи аварій, яка характеризує живучість ЕС (або окремих її частин);
λj – параметр потоку КЗ, що відбулися в j – ому елементі;
ωi – параметр потоку відмов в спрацьовуванні захисного комутаційного апарату (ЗКА) через який пройшов наскрізний аварійний струм при КЗ в j – тому елементі мережі та привів в дію його струмовий захист;
Θi – інтервал часу між діагностиками системи відключення ЗКА, у тому числі й струмовий захист;
m – число ЗКА, через які пройшов наскрізний аварійний струм і привів в дії їх струмові захисти;
r – номер енергосистеми або вузла навантаження;
n – число j – тих елементів КЗ, в яких приводить в дію i – ті ЗКА, через які пройшов наскрізний аварійний струм і привів в дію їх струмові захисти.
Чим менше Hr, тим живучість ЕС вища.
В тому випадку, якщо  ,
, 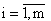 формула (1) прийме вигляд:
формула (1) прийме вигляд:
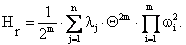 (2)
(2)
Формули (1) і (2) справедливі при виконанні наступних умов:
 (3)
(3)
– інтервали часу між КЗ і інтервали часу між виявленими відмовами в системі відключення ЗКА не суперечать експоненціальним функціям розподілу вірогідності з параметрами  і
і 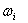 відповідно;
відповідно;
– тривалість знаходження ЗКА в незнайденому стані, що відмовив, не суперечить експоненціальній функції розподілу вірогідності;
При виведенні формул (1) і (2) були прийняті наступні допущення:
– пристрої релейного захисту (РЗ) можуть виходити з ладу тільки тоді, коли вони знаходяться в режимі очікування;
– якщо до моменту виникнення КЗ в мережі, на яке повинна реагувати РЗ, вона знаходилася в працездатному стані, то маловірогідний її вихід з ладу в режимі тривоги [7];
– відмови в схемі РЗ або приводі системи відключення ЗКА виявляються і усуваються тільки в результаті абсолютно надійних діагностичних перевірок, які відбуваються з інтервалом часу Θi.
Під відмовою в спрацьовуванні захисного комутаційного апарату (ЗКА) будемо розуміти такий, який приводить до відмови у відключенні пошкодженого елементу мережі при КЗ в зоні дії його релейного захисту [8].
Вірогідність виходу з ладу r – тої ЕС або окремих її частин:
 (4)
(4)
якщо  , то
, то  .
.
Вузлом навантаження для трансформаторної підстанції (рис. 1) може бути будь-яка з секцій шин – I або II.

Рисунок 1 - Принципова схема підстанції 110/6 – 10 кВ
Живучість вузла навантаження визначається в динамічному режимі, тобто, коли в лініяї, що відходять від секції шин, лініях або їх споживачах випадково відбуваються короткі замикання (КЗ).
Характеризувати живучість вузла навантаження будемо параметром потоку його аварійного відключення при КЗ в зоні дії струмового захисту i – го комутаційного апарату, приєднаного до відповідної секції шин.
Наприклад, якщо лінія Л1 одержує електроенергію від шини I (рис. 1), то шина I втратить живучість при збігу у просторі та часі двох випадкових подій:  – відбулося КЗ в лінії Л1 і
– відбулося КЗ в лінії Л1 і  – відбулася відмова в спрацьовуванні вимикача під номером i. В цьому випадку вимикач під номером m+2,
який забезпечує електроенергією секцію I, її відключить за допомогою струмового захисту і окрім споживача, який одержував електроенергію від секції I по лінії Л1, відключаться і всі споживачі, які одержували електроенергію від цієї секції шин через відповідні вимикачі (i=2...m).
– відбулася відмова в спрацьовуванні вимикача під номером i. В цьому випадку вимикач під номером m+2,
який забезпечує електроенергією секцію I, її відключить за допомогою струмового захисту і окрім споживача, який одержував електроенергію від секції I по лінії Л1, відключаться і всі споживачі, які одержували електроенергію від цієї секції шин через відповідні вимикачі (i=2...m).
Якщо позначити через Н1 живучість секції шин I, тобто параметр потоку аварійних відключень секції шин, при КЗ в лініях, споживачі яких одержують електроенергію від секції шин I, тоді:
 , (5)
, (5)
де
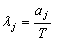 , (6)
, (6)λj – параметр потоку КЗ, що відбулися в j – тій лінії, яка приєднується до шини I через відповідний i – тий комутаційний апарат (j=1...n ), (i=1...m );
aj – число зафіксованих КЗ, які відбулися в j – тому відрізку лінії за час спостереження;
Т – час спостереження за станом ліній, які відходять від секції шин I і II і електроустаткуванням підстанції.
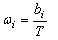 , (7)
, (7)ωi – параметр потоку відмов в спрацьовуванні системи відключення i – того ЗКА (i=1...m );
Θi – інтервали часу між діагностиками системи відключення i – того ЗКА;
bi – число виявлених в результаті діагностики пошкоджень в системі відключення ЗКА, які могли б привести до відмови його в спрацьовуванні при КЗ в зоні дії його струмового захисту.
Аналогічним чином вважається і живучість Н2 секції шин II. В цьому випадку λj – буде параметр потоку КЗ в лініях, що відходять від відповідних комутаційних апаратів, приєднаних до секції II.
Вірогідність аварійного відключення секції шин I протягом часу t можна визначити таким чином:
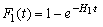 , (8)
, (8)де H1 – живучість секції I підстанції (параметр потоку аварійних відключень секції шин I при КЗ в лініях, споживачі яких одержують електроенергію від цієї секції шин).
По аналогічній формулі (8) визначається вірогідність відключення секції II підстанції, якщо відома H2.
Під спостереженням протягом Т=12 років знаходилося електрообладнання підстанції 110/6 кВ, яка забезпечувала електроенергією одну з шахт Донбасу. Від першої системи шин відходили 4 лінії і від II також 4. Схема трансформаторної підстанції аналогічна схемі (рис. 1).
За цей час було зафіксовано наступні короткі замикання (КЗ), які відбулися в лініях Л1, Л2,…, Л8:
a1=3; a2=4; a3=2; a4=6; a5=5; a6=3; a7=1;a8=0.
Системи відключення ЗКА підстанції перевірялися (діагностувалися) один раз в рік, тобто Θ=1 рік. За час спостереження 12 років було виявлене наступне число пошкоджень, які могли б привести до відмови його в спрацьовуванні при КЗ в зоні дії його струмового захисту:
b1=5; b2=4; b3=3; b4=6; b5=0; b6=0; b7=1;b8=7.
Побудувати дерево
подій і схеми мінімальних перетинів, яке пояснює втрату живучості секції I і II.
Визначити:
1) живучість секції I і II;
2) як зміниться живучість секції шин I і II, якщо діагностувати систему відключення ЗКА будемо через Θ=0,5 роки;
3) яка вірогідність того, що протягом 10 років при Θ=1 рік секції I і II втратять живучість.
Рішення. Використовуючи початкові дані прикладу формули (6), (7) знаходимо наступні параметри потоків КЗ в лініях і в системі відключення ЗКА:
а) для шин ліній, що відходять від секції:
λ1=0,25 1/рік; λ2=0,33 1/рік; λ3=0,17 1/рік; λ4=0,5 1/рік; λ5=0,42 1/рік; λ6=0,25 1/рік; λ7=0,08 1/рік; λ8=0.
б) для системи відключення ЗКА:
ω1=0,42 1/рік; ω2=0,33 1/рік; ω3=0,25 1/рік; ω4=0,5 1/рік; ω5=0; ω6=0; ω7=0,08 1/рік; ω8=0,58 1/рік;
Аналізуючи зафіксовані в оперативних журналах результати спостережень (Т=12 років) за появами КЗ в I і II лініях, що відходять від секції, виявлені і усунені в ЗКА відмови в системі відключення, які могли б привести до відмови їх в спрацьовуванні, при випадковій появі КЗ в зоні дії їх струмових защит - будуємо «дерева» і схеми мінімальних перетинів, які дозволяють пояснити втрату живучості вузлів навантаження (секція I і II) підстанції 110/6 кВ [9].
Позначимо через  – подія, відбулося КЗ в j-тій лінії;
– подія, відбулося КЗ в j-тій лінії; – подія, відбулася відмова в системі відключення i-того ЗКА.
Кожна з подій  і
і  характеризуються параметрами потоку КЗ – λj і параметром потоку відмов в системі відключення ЗКА – ωi.
характеризуються параметрами потоку КЗ – λj і параметром потоку відмов в системі відключення ЗКА – ωi.
Дерево подій, яке пояснює втрату живучості секції I і II має вид рис. 2 а, в.
Використовуючи рис. 2 а, в будуємо схеми мінімальних перетинів рис. 2 б, г.
Користуючись формулою (1), значеннями параметрів λj і ωi, одержаними за допомогою формул (2) і (3) і схемами мінімальних перетинів рис. 2 б, г знаходимо:
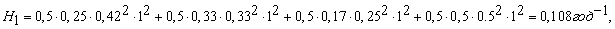

Якщо ж діагностику системи відключення ЗКА проводити через Θ=0,5 роки, тоді:
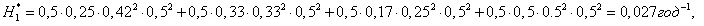



Рисунок 2 - Дерево
подій і схеми мінімальних перетинів
а) відбулася подія  – КЗ в лінії Лj (j=1...4 ) і
– КЗ в лінії Лj (j=1...4 ) і  – відмовив в спрацьовуванні ЗКА (i=1...4 );
б) схема мінімальних перетинів, складена для оцінки живучості секції I;
– відмовив в спрацьовуванні ЗКА (i=1...4 );
б) схема мінімальних перетинів, складена для оцінки живучості секції I;
в) відбулася подія  – КЗ в лінії Л7, j=7 і подію
– КЗ в лінії Л7, j=7 і подію  – відмовив в спрацьовуванні ЗКА, i=7;
г) схема мінімальних перетинів, складена для оцінки живучості секції II.
– відмовив в спрацьовуванні ЗКА, i=7;
г) схема мінімальних перетинів, складена для оцінки живучості секції II.
Визначимо у скільки разів збільшиться живучість секції шин I і II при зменшенні термінів діагностики системи відключення комутаційного апарату з Θ=1 рік на Θ=0,5 року.
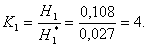
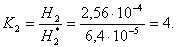
Вірогідність того, що протягом t=10 років при Θ=1 рік секції I і II підстанції втратять живучість можна оцінити за допомогою формули (8):
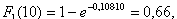
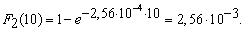
1. Для визначення найточнішої оцінки живучості вузлів навантаження підстанції 110/6 – 10 кВ, спостереження за електроустаткуваннею слід проводити не за групами однотипних елементів, а конкретно за кожною його одиницею. Чим більше час спостереження за устаткуванням підстанції, тим точніше значення живучості вузла навантаження.
2. Спостереження за роботою електроустаткуванням підстанції слід починати з моменту її пуску в експлуатацію до моменту утилізації.
3. Спостереження протягом T=12 років за електроустаткуванням підстанції 110/6 кВ, яка забезпечує електроенергією вугільну шахту, встановлено, що живучість секції шин:H1=0,108 1/рік, а H2=2,56*10-3 1/рік.
4. Показано, що зміна терміну діагностики системи відключення ЗКА 6 кВ з Θ=1 рік до Θ=0,5 року дозволяє збільшити живучість секції I і II в 4 рази.
5. Визначена вірогідність того, що протягом t=10 років секції I і II підстанції втратять живучість: F1(10)=0,66, а F2(10)=2,56*10-3.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи і матеріали по темі можуть бути одержані у автора або його керівника після вказаної дати.
- Макаров С.О. Разбор элементов, составляющих боевую силу судов.// Морской сборник, 1894,№6, с.1– 106.
- Prevention of power failures Vol. 3. Studies of the task groups on the northeast power interruption. A report to the federal power commission. June, 1967, 142 p.
- Гук Ю.Б. Теория надежности в электроэнергетике. – Л.: Энергоатомиздат. Ленинградское отд-ние, 1990. – 208 с.
- Надежность систем энергетики. Терминология. – М.: Наука, 1980,вып. 95. – 42 с.
- Ковалев А.П., Якимишина В.В. О живучести объектов энергетики//Промышленная энергетика, №1, 2006. – с. 20-26.
- Ковалев А.П, Якимишина В.В, Нагорный М.А. Оценка надежности узлов нагрузки подстанции 110/10 кВ//Промышленная энергетика, № 11, 2010. – c. 24-28.
- Фабрикант В.П. О применении теории надежности к оценке устройств релейной защиты///Электричество, № 9, 1965. – с. 6– 9.
- Эндрени Дж. Моделирование при расчётах надёжности в электроэнергетических системах. Пер. с англ./Под ред. Ю.И. Руденко. – М.: Энергоатомиздат, 1983. – 336 с.
- Диллон Б., Сингх Ч. Инженерные методы обеспечения надежности систем: Пер. с англ. – М.: Мир, 1984. – 318 с.
- Руденко Б.Н., Ушаков И.Н. Надежность систем энергетики. -М.: Наука, 1986. – 252 с.
- Китушин В. Г. Определение характеристик отказов системы при цепочечном развитии аварий. – Энергетика и транспорт, 1977, №3.
- Ковалев А.П., Чурсинов В. И., Якимишина В. В. Оценка вероятности появления цепочечных аварий в энергосистемах. – Вестник Кременчугского гос.политехн. ун-та, 2004, вып. 3/2004(26).
- Горшков В.В. Логико-вероятностный метод расчета живучести сложных систем. – Кибернетика АН УССР.-1982. № 1. – c. 104– 107.
- Стекольников Ю.И. Живучесть систем. Теоретические основы.–Санкт-Петербург: Политехника, 2002.– 155 c.
- Гук Ю.Б. Теория надежности в электроэнергетике: Учеб. Пособие для вузов. – Л.: Энергоатомиздат, 1990. – 208 с.
- Волик Б.Г., Рябинин Й.А. Эффективность, надежность и живучесть управляющих систем // Автоматика и телемеханика. – 1984.– № 12.
