Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования
- 3. Особенность расчёта
- 4. Обзор исследований по теме
- 5. Математическая модель асинхронной машины (АМ)
- 6. Реализация разработанных методов и алгоритмов в виде программы – симулятора
- Выводы
- Список источников
Введение
Обеспечение надежной и бесперебойной работы любой электростанции является одной из важнейших задач энергетики. Ее решение существенным образом зависит от создания надежной системы энергоснабжения собственных нужд. Система с.н. современной блочной электростанции и используемые в ней электродвигатели должны удовлетворять следующим требованиям:
- иметь высокую надежность схем питания с.н. в сочетании с ее гибкостью, экономичностью, а также возможностью предотвращения развития аварии;
- применяемые для привода основных механизмов котла и турбины электродвигатели большой мощности должны допускать прямой пуск;
- должен обеспечиваться успешный самозапуск электродвигателей при кратковременных перерывах питания.
В системах с.н. ТЭС и АЭС применяют асинхронные с короткозамкнутым ротором двигатели большой единичной мощности. С целью улучшения пусковых характеристик таких двигателей их ротор выполняют глубокопазным со стержнями трапецеидальной или колбовидной формы. При разработке математических моделей такого типа двигателей требуется учет эффекта вытеснения тока в роторе. Из-за указанного эффекта активное и индуктивное сопротивления зависят от частоты тока в роторе, в связи с чем их часто представляют в виде функциональных зависимостей от скольжения [4]. В таком виде схемы замещения АД могут быть использованы только для расчета стационарных и квазистационарных режимов. Поведение двигателей в переходных режимах более точно отражают многоконтурные схемы замещения, в которых ротор представлен в виде нескольких параллельно включенных RL – цепочек (контуров), параметры которых остаются постоянными независимо от частоты тока в роторе.
1. Актуальность темы
В настоящее время актуальной задачей является разработка математической модели электрической станции, позволяющей анализировать переходные процессы, возникающие при однофазных и многофазных коротких замыканиях. В терминалах защитных устройств, выполняющих обработку сигналов и прогнозирование в масштабе реального времени (РВ), возникает необходимость точного моделирования переходных процессов (ПП) с использованием расчета мгновенных величин. При разработке таких моделей составляется система дифференциальных уравнений (ДУ), описывающая исследуемую сеть, как для отдельных ее элементов, так и для их связей. Решение сложных систем дифференциальных уравнений (СДУ), имеющих место в данном случае, является возможным только с применением численных методов интегрирования. Существуют два метода разработки модели. Явный метод – используется для решения систем, включающих в себя электрические машины. Преимуществом этого метода является простота и высокая точность расчёта. Неявные методы, в свою очередь требуют пошагового решения алгебраических уравнений, что сокращает скорость расчёта, но даёт преимущество в численной устойчивости и достаточно высокой точности.Применение неявных методов численного интегрирования дифференциальных уравнений (ДУ) является более перспективным, поскольку с их помощью возможно получить устойчивое решение при моделировании многократных коммутаций в электрических сетях любой сложности.[5]
2. Цель и задачи исследования
Цель работы – разработка универсальной математической модели, предназначенной для анализа аварийных ситуаций в крупных электрических системах с учетом коммутаций, вызванных действиями устройств РЗиА.
Основные задачи исследования:
1. Совершенствование общей математической модели ММЭС на основе применения формул численного дифференцирования 1 – 6 порядка;
2. Разработка дискретных схем основных элементов ЭЭС на основе полученных матричных выражений;
3. Расчёт переходных режимов в сетях, содержащих электрические машины переменного тока, как синхронные, так и асинхронные, учитывая эффект вытеснения тока в роторах мощных ЭМ;
4. Реализация разработанных методов и алгоритмов в виде программы-симулятора
3. Особенность расчёта
Особенность расчета многократных коммутаций в ММЭС заключается в учете сильных возмущений в системе с резко различающимися постоянными времени. Этим обусловлена сложность построения математической модели, которой требуется поддерживать численную устойчивость при обеспечении необходимой точности расчета параметров состояния ЭМ.
4. Обзор исследований по теме
Для анализа режимов работы энергосистем широко применяют методы математического моделирования. Это связано с бурным развитием вычислительной техники, а также с повышением требований к точности моделирования при разработке и создании высоконадежных систем электроснабжения АЭС, ТЭС.
Представим обзор исследований и разработок по теме:
1. Глобальный. В настоящее время разработками математического моделирования переходных процессов занимаются многие фирмы, совершенствуются уже существующие программы и пакеты для создания математический моделей.
2. Национальный. Математическая модель играет важную роль не только на электрических станциях, но и на любом предприятии. Если машины будут работать непрерывно, то это поднимет потенциал Донбасса, а затем и Украины.
3. Локальный. Большинство тем магистерских и аспирантских работ кафедры ЭС связаны с математическим моделированием. Это объясняется актуальностью создания математических моделей и универсальностью их применения.
5.Математическая модель асинхронной машины (АМ)
Для математических моделей электрических машин за основу были взяты уравнения Парка-Горева с учетом эффекта вытеснения тока в пазах ротора. При формировании математической модели АМ воспользуемся классической схемой замещения [3], в которой цепи ротора представлены двумя контурами. Расчетная схема замещения АМ изображена на рис.1
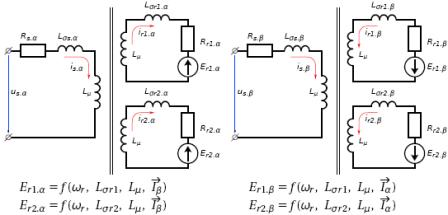
Рисунок 1 – Схемы замещения АМ для анализа переходных процессов
Система дифференциальных уравнений асинхронного электродвигателя (АЭД), записанная в неподвижной системе координат x, y , выглядит следующим образом:
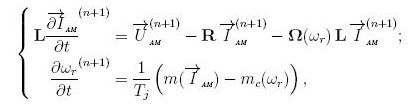
Далее составляются матрицы угловых скоростей вращения ротора и индуктивности контуров (АМ)
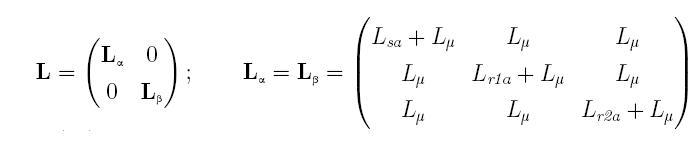
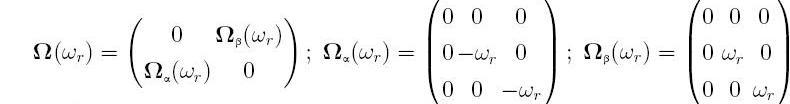
Все величины в системе уравнений рис.1 выражены в относительных единицах. Вектор переменных состояния АЭД состоит из вектора токов AM и угловой скорости:
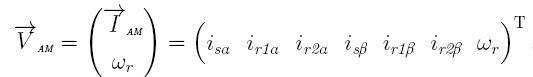
Для решения данной системы неявным методом необходимо применить формулу Гира, выполним линейные преобразования:
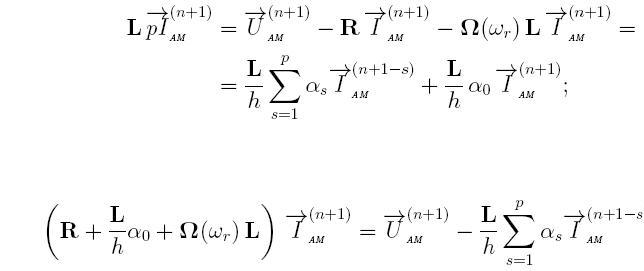
Тогда дискретная математическая модель для расчета токов всех контуров АЭД будет соответствовать выражению для обобщенной ДММ сложного элемента:
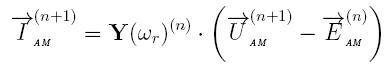
Седьмая переменная состояния, которую мы принимаем неизменной на текущем шаге, с достаточно высокой точностью вычисляется по явному методу Эйлера:
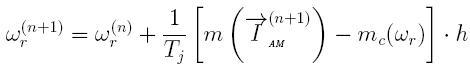
Дискретная математическая модель АЭД является составной частью ДММ основной многоузловой схемы, состоящей из двухполюсников. Согласно методу подсхем, дискретная схема замещения АМ для расчёта внешних узловых напряжений будет содержать только две эквивалентные статорные ветви, соответствующие осям x и y (рис. 2). Математическая модель АМ, приведенная к схеме замещения рис. 2 содержит только статорные величины токов и напряжений[2]:
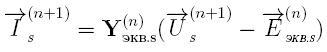
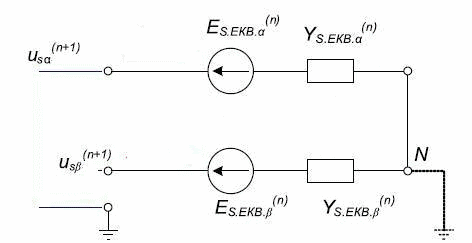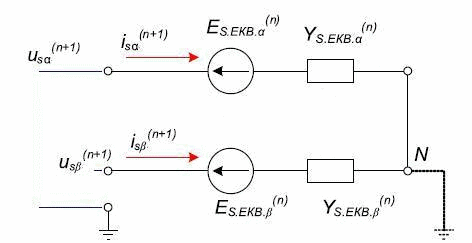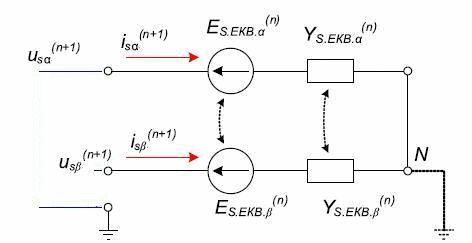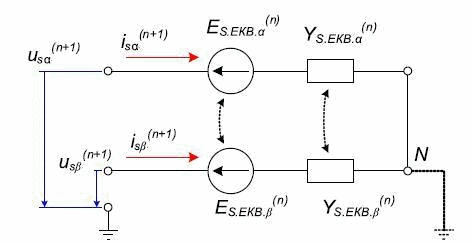
Рисунок 2 – Дискретная схема замещения эквивалентных статорных ветвей асинхронного двигателя(обмотки статора соединены в звезду)
Полученные величины интегрируются в ДММ общей схемы как блоки матрицы Yэкв.s.
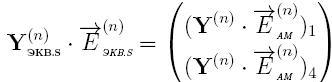
Затем выполняется расчет напряжений узлов и ветвей. По полученным статорным напряжениям (n+1)-го шага интегрирования производится расчет текущего состояния для каждой электрической машины.
6.Реализация разработанных методов и алгоритмов в виде программы – симулятора
Данная модель реализована в PowerNet. Составлена расчётная схема блока 300 мВт с учётом всех двигателей СН 6кВ.

Рисунок 3 – Cема блока 300 мВт Углегорской ТЭС
На полученных осцилограммах показаны:
1.Исследуемый двигатель привод ДВ-2, ток КЗ(подпитка от двигателя), процесс самозапуска после отключения КЗ.
2.Изменение момента двигателя при КЗ, который в нормальном режиме работал с коэффициентом загрузки 0.8
3.Процесс выбега и самозапуска при КЗ.

Рисунок 4 – Моделирование КЗ асинхронного двигателя ДВ-А2
В данном режиме было проведено исследование возникающих перенапряжений при отключении вакуумным выключателем. На срезе тока на диаграмме узла 15 виден колебательный процесс, возникающих при перенапряжениях, вызванный наличием ёмкости в сети 6кВ и индуктивности трансформатора.

Рисунок 5 – Моделирование перенапряжения АД
Выводы
Магистерская работа посвящена актуальной научной задаче моделирования переходных режимов, в том числе при многократных коммутациях. В рамках проведенных исследований выполнено:
1. Разработана дискретная схема АД , которая даёт представление о моделировании основных элементов ЭЭС на основе полученных матричных выражений.
2. Предлагаемая модель оптимизирована для применения в микропроцессорных терминалах, и реализована в специально разработанной программе для ПК с визуальным интерфейсом пользователя – PowerNet™.
3. Проведен ряд экспериментов по использованию предложенной модели, проанализированы полученные результаты.
Дальнейшие исследования направлены на следующие аспекты:
В дальнейшем планируется внедрение моделей как отдельных агрегатов, так и при их взаимосвязи в различных схемах электрических соединений, расчёт несимметричных КЗ, насыщение трансформаторов и автотрансформаторов.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2012 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- В.Ф. Сивокобыленко, В.К. Лебедев Переходные процессы в системах электроснабжения собственных нужд электростанций: Учеб. Пособие. – Донецк: ДонНТУ, 2002. – 136 с.
- В.Ф. Сивокобыленко, П.А. Харченко Динамическое преобразование схем замещения электрических систем при моделировании переходных процессов: Сборник статей Донецкого национального технического университета. Электротехника и энергетика.– Донецк: ДонНТУ, 2009
- В.Н. Винославский, Г.Г. Пивняк, Л.И. Несен и др. Переходные процессы в системах электроснабжения: Учебник / Под ред. В. Н. Винославского. К.: Выща шк. Головное изд-во, 1989. – 422 с.
- В.Ф. Сивокобыленко, В.И. Костенко Математическое моделирование электродвигателей собственных нужд электрических станций. Учебное пособие. – Донецк: ДПИ, 1979. – 110с.
- М.С. Сегеда Математичне моделювання в електроенергетиці: [Навч.посіб. для студентів електроенерг. спец.] / М. С. Сегеда. Львів: Нац. ун-т «Львів. політехніка», 2002. – 299 c.
- И.П. Крючков Переходные процессы в электроэнергетических системах / И. П. Крючков. 2008. – 416 с.
- В.С. Перхач Математические задачи электроэнергетики / В.С. Перхач. Л.: «Высшая школа», 1989. – 464 с.
