Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і завдання дослідження
- 3. Особливість розрахунку
- 4. Огляд досліджень по темі
- 5. Математіческая модель асинхронної машини (АМ)
- 6. Реалізація розроблених методів та алгоритмів у вигляді програми – симулятора
- Висновки
- Перелік посилань
Вступ
Забезпечення надійної та безперебійної роботи будь-якої електростанції є однією з найважливіших задач енергетики. Її рішення істотно залежить від створення надійної системи енергопостачання власних потреб. Система в.п. сучасної блочної електростанції і використовувані в ній електродвигуни повинні відповідати таким вимогам:
- мати високу надійність схем живлення в.п. в поєднанні з її гнучкістю, економічністю, а також можливістю запобігання розвитку аварії;
- застосовувані для приводу основних механізмів котла і турбіни електродвигуни великої потужності повинні допускати прямий пуск;
- повинен забезпечуватися успішний самозапуск електродвигунів при короткочасних перервах живлення.
Досвід експлуатації показує, що невиконання зазначених вимог може являтися причиною виходу з ладу блочного агрегату і створення аварійних ситуацій в енергосистемі.
В системах в.п. ТЕС і АЕС застосовують асинхронні з короткозамкненим ротором двигуни великої одиничної потужності. З метою поліпшення пускових характеристик таких двигунів їх ротор виконують глубокопазним зі стержнями трапецеїдальної або колбовідної форми. При розробці математичних моделей такого типу двигунів потрібно зазначити ефект витіснення струму в роторі. Через зазначеного ефекту активне і індуктивний опори залежать від частоти струму в роторі, в зв'язку з чим їх часто представляють у вигляді функціональних залежностей від ковзання [4]. У такому вигляді схеми заміщення АД можуть бути використані тільки для розрахунку стаціонарних і квазістаціонарних режимів. Поведінку двигунів в перехідних режимах більш точно відображають багатоконтурні схеми заміщення, в яких ротор представлений у вигляді декількох паралельно включених RL-ланцюжків (контурів), параметри яких залишаються постійними незалежно від частоти струму в роторі.
1. Актуальність теми
В даний час актуальним завданням є розробка математичної моделі електричної станції, що дозволяє аналізувати перехідні процеси, що виникають при однофазних і багатофазних коротких замиканнях. В терміналах захисних пристроїв, що виконують обробку сигналів і прогнозування в масштабі реального часу (РЧ), виникає необхідність точного моделювання перехідних процесів (ПП) з використанням розрахунку миттєвих величин. При розробці таких моделей складається система диференційних рівнянь (ДР), що описує досліджувану мережу, як для окремих її елементів, так і для їх зв'язків. Рішення складних систем диференціальних рівнянь (СДР), що мають місце в даному випадку, є можливим тільки із застосуванням чисельних методів інтегрування. Існують два методи розробки моделі. Явний метод – використовується для вирішення систем, що включають в себе електричні машини. Перевагою цього методу є простота і висока точність розрахунку. Неявні методи, в свою чергу вимагають покрокового рішення алгебраїчних рівнянь, що скорочує швидкість розрахунку, але дає перевагу в чисельної стійкості і досить високою точності.Використання неявних методів чисельного інтегрування диференціальних рівнянь (ДР) є більш перспективним, оскільки з їх допомогою можливо отримати стійке рішення при моделюванні багатократних комутацій в електричних мережах будь-якої складності.[5]
2. Мета і завдання дослідження
Мета роботи – розробка універсальної математичної моделі, призначеної для аналізу аварійних ситуацій у великих електричних системах з урахуванням комутацій, викликаних діями пристроїв РЗіА.
Основні завдання дослідження:
1. Удосконалення загальної математичної моделі ММЕС на основі застосування формул чисельного диференціювання 1 – 6 порядку;
2. Розробка дискретних схем основних елементів ЕЕС на основі отриманих матричних виразів;
3. Розрахунок перехідних режимів в мережах, що містять електричні машини змінного струму, як синхронні, так і асинхронні, враховуючи ефект витіснення струму в роторах потужних ЕМ;
4. Реалізація розроблених методів та алгоритмів у вигляді програми-симулятора
3. Особливість розрахунку
Особливість розрахунку багаторазових комутацій в ММЕС полягає в обліку сильних збурень в системі з постійними часу, які різко відрізняються. Цим обумовлена складність побудови математичної моделі, якій потрібно підтримувати чисельну стійкість при забезпеченні необхідної точності розрахунку параметрів стану ЕМ.
4. Огляд досліджень по темі
Для аналізу режимів роботи енергосистем широко застосовують методи математичного моделювання. Це пов'язано з бурхливим розвитком обчислювальної техніки, а також з підвищенням вимог до точності моделювання при розробці та створенні високонадійних систем електропостачання АЕС, ТЕС.
Представимо огляд досліджень і розробок по темі:
1. Глобальний. В даний час розробками математичного моделювання перехідних процесів займаються багато фірм, вдосконалюються вже існуючі програми та пакети для створення математичний моделей.
2. Національний. Математична модель грає важливу роль не тільки на електричних станціях, але й на будь-якому підприємстві. Якщо машини будуть працювати безперервно, то це підніме потенціал Донбасу, а потім і України.
3. Локальний. Більшість тем магістерських та аспірантських робіт кафедри ЕС пов'язані з математичним моделюванням. Це пояснюється актуальністю створення математичних моделей і універсальністю їх застосування.
5.Математична модель асинхронної машини (АМ)
Для математичних моделей електричних машин за основу були взяті рівняння Парка-Горєва з урахуванням ефекту витіснення струму в пазах ротора. При формуванні математичної моделі АМ скористаємося класичною схемою заміщення [3], в якій ланцюги ротора представлені двома контурами. Розрахункова схема заміщення АМ зображена на рис.1
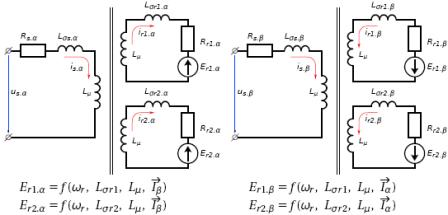
Рисунок 1 – Схеми заміщення АМ для аналізу перехідних процесів
Система диференціальних рівнянь асинхронного електродвигуна (АЕД), записана в нерухомій системі координат x, y, виглядає наступним чином:
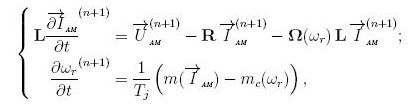
Далі складаються матриці кутових швидкостей обертання ротора й індуктивності контурів (АМ)
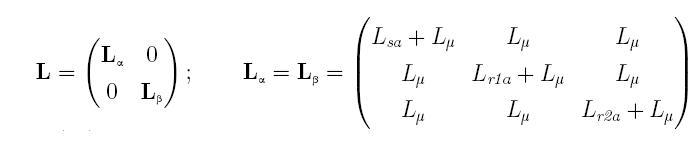
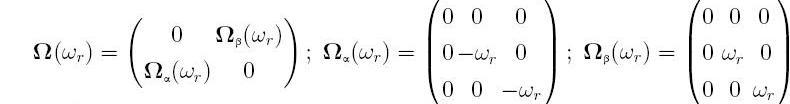
Всі величини в системі рівнянь рис.1 виражені у відносних одиницях. Вектор змінних стану АЕД складається з вектора струмів AM і кутовий швидкості:
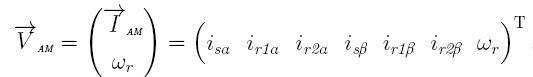
Для вирішення даної системи неявним методом необхідно застосувати формулу Гіра, виконаємо лінійні перетворення:
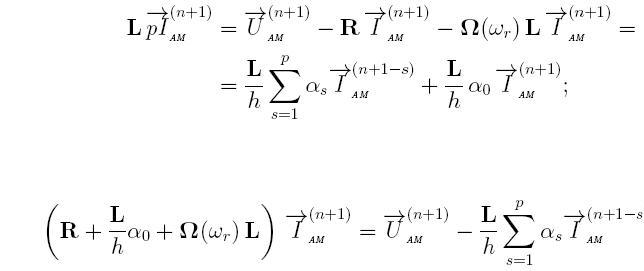
Тоді дискретна математична модель для розрахунку струмів всіх контурів АЕД буде відповідати виразам для узагальненої ДММ складного елементу:
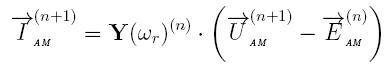
Сьома відмінна стану, яку ми приймаємо незмінною на поточному кроці, з досить високою точністю обчислюється по явному методу Ейлера:
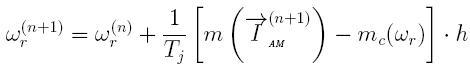
Дискретна математична модель АЕД є складовою частиною ДММ основний многоузловой схеми, що складається з двополюсників. Згідно з методом подсхем, дискретна схема заміщення АМ для розрахунку зовнішніх вузлових напруг буде містити тільки дві еквівалентні статорні гілки, відповідні осях x і y (рис. 2). Математична модель АМ, наведена до схеми заміщення рис. 2 містить тільки статорні величини струмів і напруг [2]:
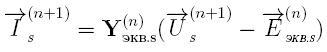
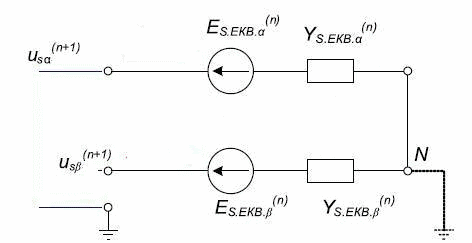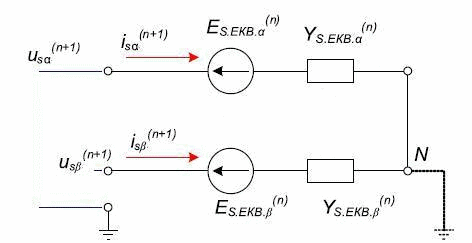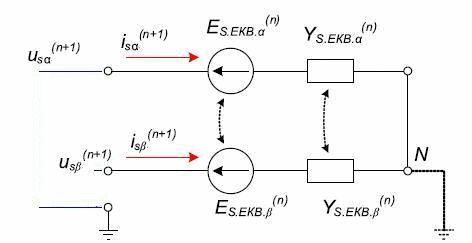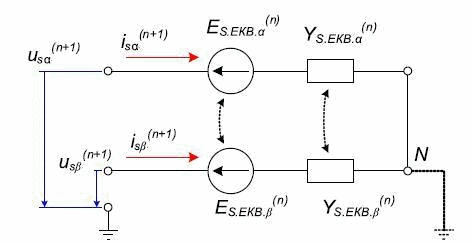
Рисунок 2 – Дискретна схема заміщення еквівалентних статорних гілок асинхронного двигуна(обмотки статора з'яднані у зірку)
Отримані величини інтегруються в ДММ загальної схеми як блоки матриці Yэкв.s.
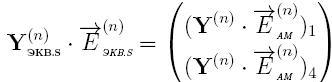
Потім виконується розрахунок напруг вузлів і гілок. За отриманими статорні напруженням (n +1)-го кроку інтегрування проводиться розрахунок поточного стану для кожної електричної машини.
6.Реалізація розроблених методів та алгоритмів у вигляді програми – симулятора
Дана модель реалізована в PowerNet. Складена розрахункова схема блоку 300 МВт з урахуванням всіх двигунів СН 6кВ

Рисунок 3 – Cема блоку 300 мВт Углегорської ТЕС
На отриманих осцілограммах показані:
1.Досліджуваний двигун привід ДВ-2, струм КЗ (підживлення від двигуна), процес самозапуску після відключення КЗ.
2.Зміна моменту двигуна при КЗ, який в нормальному режимі працював з коефіцієнтом навантаження 0.8
3.Процеси вибігу і самозапуску при КЗ.

Рисунок 3 – Моделювання КЗ асинхронного двигуна ДВ-А2
В даному режимі було проведено дослідження перенапруг при відключенні вакуумним вимикачем. На зрізі струму на діаграмі вузла 15 видно коливальний процес, що виникає при перенапруженнях, викликаних наявністю ємності в мережі 6кВ й індуктивності трансформатора.

Рисунок 5 – Моделювання перенапруги АД
Висновки
Магістерська робота присвячена актуальній науковій задачі моделювання перехідних режимів, у тому числі при багаторазових комутаціях. У рамках проведених досліджень виконано:
1. Розроблена дискретна схема АД, яка дає уявлення про моделювання основних елементів ЕЕС на основі отриманих матричних виразів.
2. Запропонована модель оптимізована для застосування в мікропроцесорних терміналах, і реалізована в спеціально розробленою програмою для ПК з візуальним інтерфейсом користувача – PowerNet ™.
3. Проведено ряд експериментів з використання запропонованої моделі, проаналізовано отримані результати.
Подальші дослідження спрямовані на наступні аспекти:
Надалі планується впровадження моделей як окремих агрегатів, так і при їх взаємозв'язку в різних схемах електричних з'єднань, розрахунок несиметричних КЗ, насичення трансформаторів і автотрансформаторів.
При написанні даного реферату магістерська робота ще не виконана. Остаточне завершення: грудень 2012 року. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Перелік посилань
- В.Ф. Сивокобыленко, В.К. Лебедев Переходные процессы в системах электроснабжения собственных нужд электростанций: Учеб. Пособие. – Донецк: ДонНТУ, 2002. – 136 с.
- В.Ф. Сивокобыленко, П.А. Харченко Динамическое преобразование схем замещения электрических систем при моделировании переходных процессов: Сборник статей Донецкого национального технического университета. Электротехника и энергетика.– Донецк: ДонНТУ, 2009
- В.Н. Винославский, Г.Г. Пивняк, Л.И. Несен и др. Переходные процессы в системах электроснабжения: Учебник / Под ред. В. Н. Винославского. К.: Выща шк. Головное изд-во, 1989. – 422 с.
- В.Ф. Сивокобыленко, В.И. Костенко Математическое моделирование электродвигателей собственных нужд электрических станций. Учебное пособие. – Донецк: ДПИ, 1979. – 110с.
- М.С. Сегеда Математическое моделирование в электроэнергетике / М. С. Сегеда. Львов: Нац. ун-т «Львов. политехника», 2002.– 299 c.
- И.П. Крючков Переходные процессы в электроэнергетических системах / И. П. Крючков. 2008. – 416 с.
- В.С. Перхач Математические задачи электроэнергетики / В.С. Перхач. Л.: «Высшая школа», 1989. – 464 с.
