Abstract
Content
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- 3. The peculiarity of the calculation
- 4. Mathematical model of asynchronous machine
- Conclusion
- References
Introduction
Ensuring reliable and uninterrupted operation of any power plant is one of the biggest challenges of energy. Its solution depends significantly on the creation of a reliable energy supply their own needs. System SN modern block used in power plants and electric motors it must meet the following requirements:
- have a high reliability of power supply circuits sc combined with its flexibility, efficiency, and ability to prevent the development of the accident;
- used to drive the basic mechanisms of the boiler and turbine motors have high power to allow direct start;
- should be assured a successful self-starting electric power for short periods of time.
In the systems of their own needs to use asynchronous squirrel cage motors with large unit capacity. In order to improve the starting characteristics of such engines to the rotor operates a rod or cone-shaped trapezoidal shape. In developing mathematical models of this type of engine requires consideration of the effect of displacement current in the rotor. Because of this effect active and inductive resistance depends on the frequency of the current in the rotor, and therefore they are often in the form of functional dependencies from sliding [4]. As such, the equivalent circuit can only be used for the calculation of stationary and quasistationary regimes. The behavior of the engine under transient conditions more accurately reflect the multiloop equivalent circuit in which the rotor is presented in the form of several parallel-connected RL - chains (loops), whose parameters remain constant regardless of the frequency of the current in the rotor.
1. Theme urgency
At present, an urgent task is to develop a mathematical model of the power station, which allows to analyze the transients that occur during single-and multi-phase short circuits. In the terminals of protective devices that perform signal processing and prediction in real time (RT), there is a need for accurate modeling of transient processes (PP) using the calculation of the instantaneous values. In developing such models is a system of differential equations (DE), describing the studied network, both for its individual elements, and for their relations. Addressing the complex systems of differential equations (SDE), which occur in this case is only possible with the use of numerical integration methods. There are two methods of model development. Explicit method - is used for solving systems that include electric cars. The advantage of this method is its simplicity and high accuracy of calculation. Implicit methods, in turn, require a step solutions of algebraic equations, which reduces the speed of calculation, but it gives an advantage in numerical stability and relatively high tochnosti.Primenenie implicit methods for the numerical integration of differential equations (DE) is more promising, because with their help, maybe get a stable solution the simulation of multiple cycles in networks of any complexity.[5]
2. Goal and tasks of the research
Goal – development of a universal mathematical model, designed for the analysis of accidents in large electrical systems, taking into account switching caused by the actions of devices RZiA.
Tasks of the research:
1. Improving the general mathematical model MMES by applying numerical differentiation formulas 1 – 6 of the order;
2. The development of digital circuits the basic elements of the EPS on the basis of the matrix expressions;
3. Calculation of transients in networks that contain electrical machinery AC both synchronous and asynchronous, taking into account the effect of current displacement in the rotors of powerful EM;
4. Implementation of the developed methods and algorithms in a simulator program
3. The peculiarity of the calculation
The peculiarity of the calculation of multiple switches in a MMES is taken into account the strong perturbations in the system with very different time constants. This is due to the difficulty of constructing a mathematical model, which is required to maintain numerical stability, while ensuring the necessary accuracy of calculation of parameters of the state of EM.
4.Mathematical model of asynchronous machine(АМ)
For the mathematical models of electrical machines was based on the equation of the Park-Gorev with the effect of current displacement in the grooves the rotor. In forming the mathematical model, we use the classical AM equivalent circuit [3], in which the rotor circuit are two circuits. The calculated equivalent circuit shown in Fig. 1
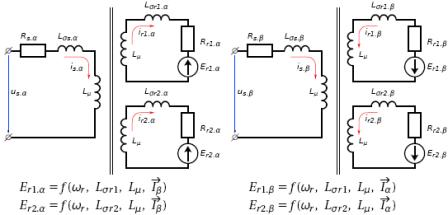
Fig. 1 – Equivalent circuit of the AM
The system of differential equations of induction motor, recorded in the fixed system of coordinates x, y, as follows:
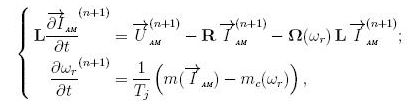
Further, the matrix composed of angular velocities of rotation of the rotor and inductor circuits
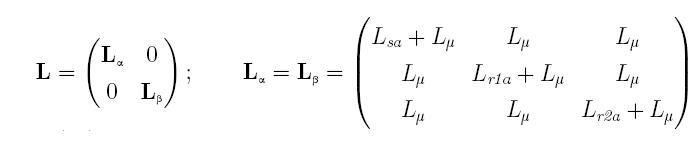
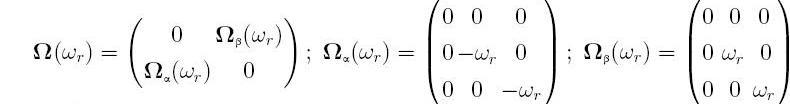
All values in the system of equations of Figure 1 are expressed in relative units. The vector of state variables EDA consists of the vector currents AM and the angular velocity:
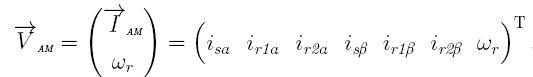
To solve this system of implicit method must be apply the formula Gere, perform linear transformations:
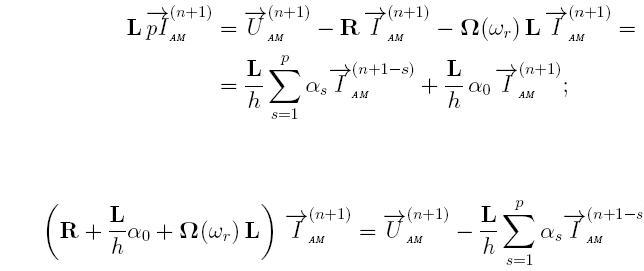
Then the discrete mathematical model for calculating the current contours of the EDA will match the expression for the generalized complex element DMM:
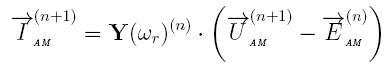
The seventh state variable, which we assume constant at the current step, with a fairly high degree of accuracy is calculated by explicit Euler method:
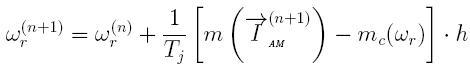
A discrete mathematical model of the EDA is an integral part DMM multi-core scheme, consisting of two-terminal networks. According to the method of sub-schemes, the discrete equivalent circuit of the AM for the calculation of the external node voltages will contain only two equivalent stator branches, corresponding to the x and y (Fig. 2). A mathematical model of the AM, reduced to the equivalent circuit in Fig. 2 contains only values of stator currents and voltages [2]:
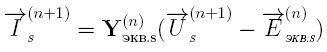
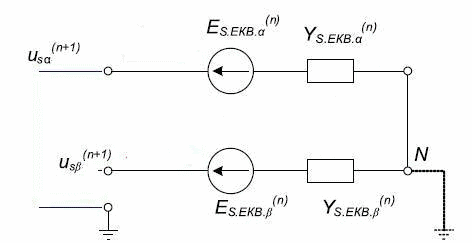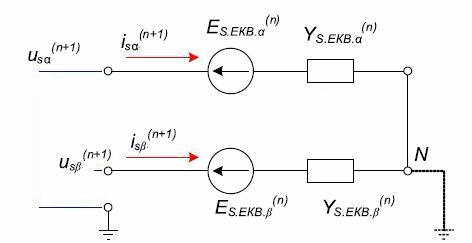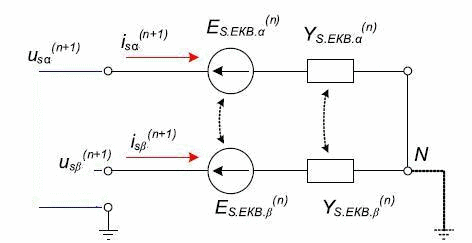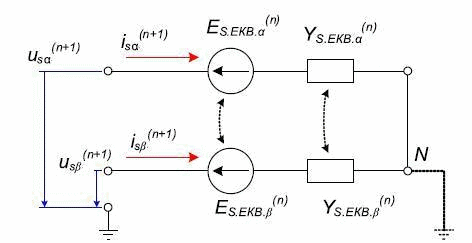
Fig.2 – The discrete equivalent circuit of the stator branches
The obtained values are integrated into the overall scheme of DMM as blocks of the matrix Yekv.s.
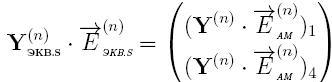
It then calculated the stress of nodes and branches. According to the obtained stator voltages (n +1)-th integration step is calculated for each of the current state of the machine.
Conclusion
Master's thesis is devoted to actual scientific problem of modeling the transition regimes, including the multiple commutations. In the trials carried out:
1. Developed discrete circuitry in blood pressure, which gives an idea of modeling the main elements of the EPS on the basis of the matrix expressions.
2. The proposed model is optimized for use in microprocessor-based terminals, and implemented in a specially designed program for the PC with a visual user interface - PowerNet ™.
3. A number of experiments on the use of the proposed model, analyzed the results.
Further research focuses on the following aspects:
In the future we plan to implement models of individual units, and in their relationships in a variety of wiring schemes, the calculation of asymmetrical short-circuit, the saturation of transformers and autotransformers.
This master's work is not completed yet. Final completion: December 2012. The full text of the work and materials on the topic can be obtained from the author or his head after this date.
References
- В.Ф. Сивокобыленко, В.К. Лебедев Переходные процессы в системах электроснабжения собственных нужд электростанций: Учеб. Пособие. – Донецк: ДонНТУ, 2002. – 136 с.
- В.Ф. Сивокобыленко, П.А. Харченко Динамическое преобразование схем замещения электрических систем при моделировании переходных процессов: Сборник статей Донецкого национального технического университета. Электротехника и энергетика. – Донецк: ДонНТУ, 2009
- В.Н. Винославский, Г.Г. Пивняк, Л.И. Несен и др. Переходные процессы в системах электроснабжения: Учебник / Под ред. В. Н. Винославского. К.: Выща шк. Головное изд-во, 1989. – 422 с.
- В.Ф. Сивокобыленко, В.И. Костенко Математическое моделирование электродвигателей собственных нужд электрических станций. Учебное пособие. – Донецк: ДПИ, 1979. – 110с.
- М.С. Сегеда Математическое моделирование в электроэнергетике / М. С. Сегеда. Львов: Нац. ун-т «Львов. политехника», 2002.– 299c.
- И.П. Крючков Переходные процессы в электроэнергетических системах / И. П. Крючков. 2008. – 416 с.
- В.С. Перхач Математические задачи электроэнергетики / В.С. Перхач. Л.: «Высшая школа», 1989. – 464 с.
