DonNTU   Masters' portal

Abstract

Content

Introduction

Electromagnetic compatibility (EMC) (electromagnetic compatibility – EMC) – is the ability of the technical tools to operate effectively with a given quality to some of the electromagnetic environment without creating intolerable electromagnetic disturbances to other facilities. At present, the industrial enterprises is rising steadily and power for power consumers, creating a variety of electromagnetic interference (EMI), which propagates in air, and on the conductors of electric current, have a different impact to power-consuming equipment and systems of control, protection, computers and automation [2].

Issues of power quality (PQ) were a significant development in most aspects of this multifaceted problem. Its importance, especially in economic terms, it became clear to both producers and consumers of electricity (EP).

Thus, in the USA – losses due to low power quality at several tens of billions of dollars a year. The study of this problem, carried out at the end of 80 years in the EPS companies of the former USSR, showed that the annual cost in the industry due to the low PQ is about 10 mlrd.dol/year, with more than 10% of the damage falls on its technological component. In the USA, losses associated with the violation of safety of EPS, reaching 25 – 30 mlrd.dol. a year, and, according to experts violation of the reliability of electricity supply in some cases associated with reduced PQ [8].

Therefore, the challenge of working together of various power consumers, of EMC, with each passing year it becomes more urgent.

1. Practical and scientific relevance of the topic

Practical relevance is to develop a reliable methodology for assessing asymmetry when operating electric arc furnace (EAF), as violation of EMC leads to unnecessary increase in the capital, and an understatement – to the detriment of the additional energy losses, reducing the life of electrical equipment, deterioration of product quality. In this regard, the high requirements for validity and accuracy of both methods for estimating the EMC at the design stage and in the operation of power systems. Damages for breach of EMC in Ukraine amounts to 1 billion dollars a year.

As in the existing networks are random noise processes, requires the development of general methods of analysis. Existing methods use static models related to the slow change in voltage, which is not suitable for evaluation of asymmetry in the work of the EAF when the voltage is changing rapidly. This problem is solved using a dynamic simulation of the impacts of noise on the electrical equipment. Therefore, the scientific relevance of the work is to ensure the reliability of estimates of EMC.

2. Goal and objectives

Goal of the work – asymmetry of the experimental evaluation of the records the instantaneous phase voltages and currents EAF obtained with a digital oscilloscope REKON.


We must tackle the following tasks:

  1. Verification of the possibility of calculating the asymmetry of the records and linear phase voltages;
  2. Plotting negative sequence voltage;
  3. Check if the zero sequence in the three-wire networks from experimental data;
  4. Assessing the impact of asymmetry in the three-phase induction and synchronous motors (blood pressure and diabetes);
  5. Verification of the Standard at the operating company.

3. The concept of asymmetry voltage

Asymmetry voltage is the most common conductive EMC interference. In power systems, industrial voltage unbalance can be caused by external and internal factors. External asymmetry is due, in first, that the generators at power plants can not create a completely symmetrical system of voltages. In the second, lines and transformers are spread in the resistances of the phases and the transformation coefficients. Third, to the neighboring plants can be so powerful consumers with an asymmetric load (EAF, single furnace, traction substations, etc.) that they create asymmetry in the regional power networks, which is powered by the enterprise in question. In design it is assumed that no external asymmetry [1].

The source of the internal three-phase asymmetry are power-consuming equipment with asymmetric load (EAF, magnetic hydraulic systems for precision casting, etc.), as well as single-phase power-consuming equipment.

In most publications, estimation of asymmetric modes is made for special cases of constant and periodic distortions of the asymmetry of the voltage curve. However, in existing networks, noise is a random process, asymmetry varies over time. For example, when EAF:

Figure 1 – Load phase (a-c) and the negative sequence current (d) for the work of particleboard capacity of 100 tons during the melting

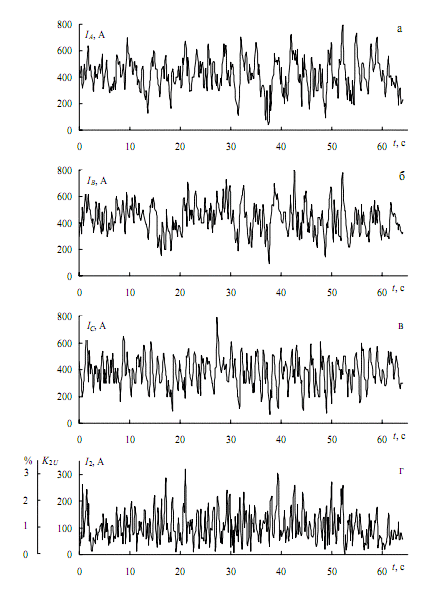
Figure 1 – Load phase (a-c) and the negative sequence current (d) for the work of particleboard capacity of 100 tons during the melting

Therefore, evaluation of EMC on the asymmetry requires the development of general methods of analysis.

System for moving the electrode in the EAF to operate independently of each other, so that the phase currents are not equal to each other, which creates asymmetry in the voltage electricity grid. The asymmetry of the most effect on blood pressure and diabetes. The standard three-second normalized asymmetry coefficients in the total points of adhesion, which are used in the calculation of consumption of commercial energy sources and to identify violations of EMC. However, it is impossible to assess the negative impact of asymmetry on the specific power-consuming equipment (for blood pressure and diabetes). For existing businesses need to have charts of symmetrical components, which can be obtained from the experimental records of stress [1].

4. Input

The initial data are graphs of phase voltages and currents particleboard produced during melting (in the beginning, middle and end of melting). Recording was carried out in one of the steelworks steel plant with a digital oscilloscope REKON. The recording time was 29 s, The values were recorded for every 0,0005 s, which amounted to 58000 values for each parameter record.

5. Normalization of asymmetry according to State Standard 13109 – 97

According to [3] asymmetry voltage is as follows:

First, determine the rms voltage direct, inverse and zero sequence fundamental frequency according to the formulas:

pic2 pic3 pic4

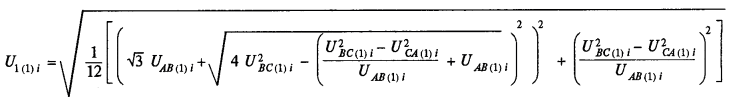
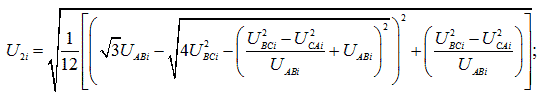
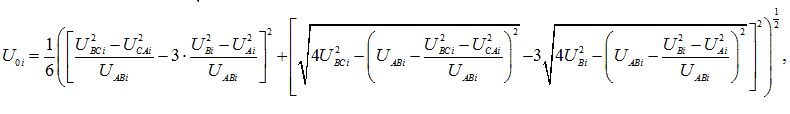
where UAB(1)i, UBC(1)i, UCA(1)i – line to line voltage rms values of the fundamental frequency in the i-th observation, V, kV;

Asymmetry voltage on the negative and zero sequences К2Ui and К0Ui calculated as a percentage as a result of the i-th observation by the formulas:

pic5 pic6

where U2(1)i, U0(1)i – rms voltage feedback and zero-sequence fundamental frequency three-phase voltage system in the i-th observation, V, kV;

U1(1)i – rms voltage positive sequence fundamental frequency in the i-th observation, V, kV.

6. The test calculation of the asymmetry on the record phase and line voltages

As a result of experience with a digital recorder REKON recorded phase voltages. The question arises, can be considered indicators of asymmetry between phases (linear) voltages?

Consider an example where the neutral point O and O' are the same load (load does not shift the neutral point).

We define the amplitude of phase voltage UA = 220 V, UB = 0,5·UA = 0,5·220 = 110 V, the angle between the vectors of phase voltages UA и UB accepted 120°.

We construct a vector diagram (VD) phase and linear voltages

VD phase and linear voltages

VD phase and linear voltages

We write the phase voltages in complex form:

pic8

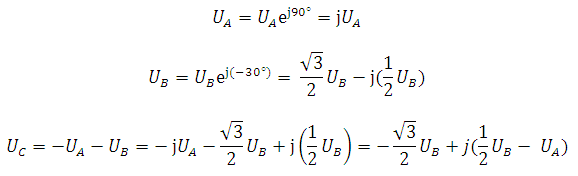
The expressions for the interphase stresses:

pic9

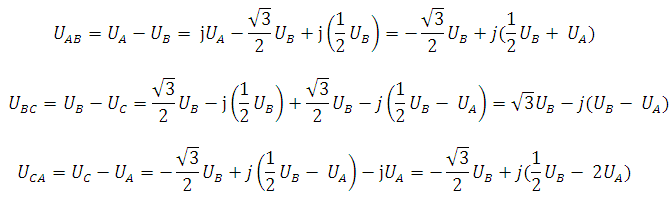
After substitution of the amplitude of phase voltage UA = 220 V и UB = 0,5·UA = 0,5·220 = 110 V recorded in the above expression we obtain:

UC, В UAB, В UBC, В UCA, В
190,5256 291,0326 220 396,6106

According to [3] acting values of the stresses forward U1 and reverse U2 sequences from the values of phase and line voltages:

По фазным напряжениям По линейным напряжениям
U1, В U2, В U1, В U2, В
168,0278 63,50853 291,0326 110

Coefficient of asymmetry voltage of the reverse sequence К2Ui:

The obtained values of the coefficients of asymmetry of stress in the reverse sequence match, so can be considered as indicators of unbalance of phase and line voltages. But if the load point O' is displaced, the calculation of the linear stress is not allowed.

7. Standardized EMC for asymmetry voltage

Initially, the standards of different countries were normalized only allowable values of the asymmetry. These rules have a clear meaning only for the special case of constant asymmetry, when in the static model, the coefficient of asymmetry can uniquely determine the EMC performance. The next step was the introduction of rules on short-term changes in asymmetry: the level of asymmetry was set from 1 to 3%, and briefly permitted unbalance of 2 to 5%. For the short duration of diabetes indicated the increasing asymmetry of 1  min. Since 1981, the permissible asymmetry assessed beginning with an integral 95%, was used for normalization of the principle of the practical certainty [1].

In [3] normalized rms values of the coefficients of three-second unbalance. In the notation does not distinguish between current and average values: K2Ui – i-th current and К2U – averaged, as well as between the measured (or determinable) and normalized values. We use the following notation: [Θ] = 3 s – standardized cumulative duration (in [3] – is denoted by Tνs); K2U, K2ωΘ, K2ω[Θ] – current, cumulative and reduced coefficients of three-second unbalance.

In [3] adopted a discrete averaging on the adjoining three-second intervals. At each interval of N ordinates taken – at least 9. Sampling will be 3/(N + 1) – less than 0,3 s, if N is not taken into account in the final or initial ordinate. The cumulative rate asymmetry:

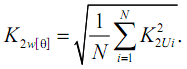
pic12
(1)

The control asymmetry voltage is carried out at night, the number of three-second intervals is large, so the condition of stationarity of the process of discrete averaging yields the same result as continuous:

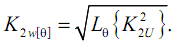
pic13
(2)

The calculated maximum values of K2[Θ]н max and K2[Θ]п max for the normal modes and the limit defined by the boundary probabilities 0,05 and 0,001, shall not exceed the corresponding allowable values ([] in the notation):

pic14
(3)

that in [3] are assumed to be 2 and 4 % [1].

Formally, the transformation (2) corresponds to a "cumulative" standard for power consumers. The absence of the factor before the sum in (1) means that the EMC model (fig. 2, a), there is no need to introduce a weighting filter (WF) – its transmission coefficient is unity. Quad 1 and 3 form a link of the cumulative quadratic cumulative process:

pic15
(4)

EMC performance computing unit (PE) includes a link 7 and the square root calculation unit 8 define the maximum values with a given probability of a boundary [1].

Figure 2 – Block diagram of the standard model for power consumers on the asymmetry of stress: a – cumulative, b – inertial

Figure 2 – Block diagram of the standard model for power consumers on the asymmetry of stress: a – cumulative, b – inertial

8. The calculation of cumulative asymmetry coefficients for the interference graph

These cumulative factors unbalance voltage K2ωΘ duration [Θ] = 3 s are calculated to verify compliance with the norms of the standard [3]. The calculation is required only in two cases. The first, if the largest value K2UM not exceed 2%, the requirements of the standard is certainly satisfied. The second since the cumulative three-second maximum can not be greater than the effective values of the asymmetry, then

pic17
(1)

clearly violated the requirements of the standard [1].

Before calculating the coefficients on schedule asymmetry appropriate to verify the condition:

pic18
(2)

If it is not broken, instead of a quadratic cumulative averaging just run three-second averaging of the original schedule, rather than its square.

Averaging is performed as follows. The original schedule is squared (fig. 3, curve 1). When Θ = 0 the averaging interval to the left of the vertical axis, not capturing graph. Therefore, averaged over the interval value is zero – as it relates to the end of the interval, to t = 0. Then the averaging interval is shifted to step Δ to the right, grabbing the initial ordinate K22U(0). The average value of Δ·K22U(0)/[Θ] is the time t = Δ. The interval is shifted back one step Δ, etc. The resulting cumulative process energy ω2Θ[t] is shown in fig. 3 by curve 2. Extracting from the ordinates of the square root of the graph, we obtain the desired process (curve 3) [1].

Figure 3 – Determination of three-second graph of the cumulative coefficients of asymmetry of the stress at work EAF-100

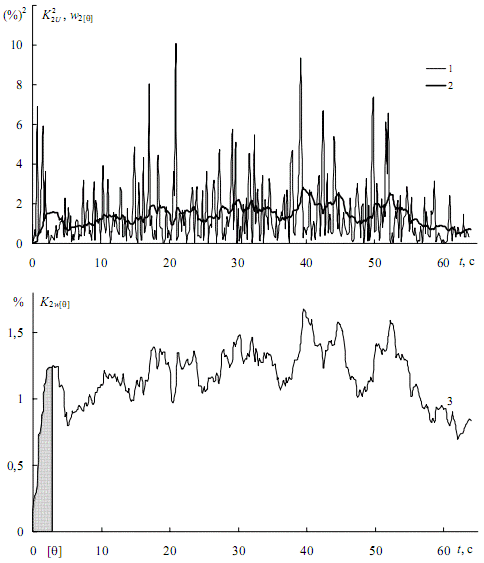
Figure 3 – Determination of three-second graph of the cumulative coefficients of asymmetry of the stress at work EAF-100

In the initial part of the random transition takes place. From fig. 3 (a broken line) that this process is completely ends exactly 3 s. Discarding part of the graph from 0 to 3 (shaded area), we obtain a graph of the stationary regime. For this we compute the effective value of K2[Θ]э and the standard σ2[Θ], and construct the distribution function F(K2ω[Θ]), shown in fig. 4 curve 1. For comparison, shows the distribution function of the original graph (curve 2). Since averaging smooths out the graph, the curve of a less flat than the curve of 2 [1].

Figure 4 – The distribution function of voltage unbalance factors at work DSP-100: 1 – three-second, 2 – source

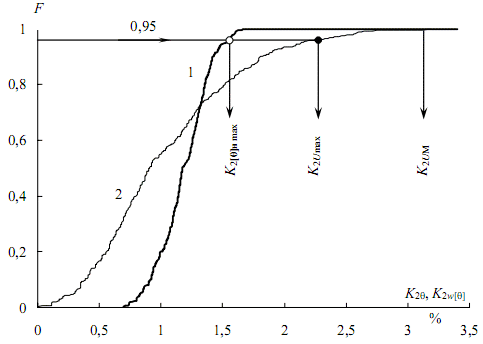
Figure 4 – The distribution function of voltage unbalance factors at work DSP-100: 1 – three-second, 2 – source

To determine the maximum calculated values of the asymmetry in the normal K2[Θ]н max draw a horizontal 0,95 to its intersection with the graph of the distribution function (light circle). If this value is less than 2%, then the requirement of the standard is not violated. Estimate the maximum initial schedule K2Umax (dark circle) is greater than a three-second. This indicates that the evaluation of the admissibility of asymmetry in the static model, without averaging, is unacceptable.

Checking the implementation of standards for limiting regime does not produce, as the greatest ordinate of the initial schedule does not exceed 4%.

The correlation function of the coefficients of asymmetry does not contain a periodic component, so no need to calculate the cumulative values of the maxima for Θ smaller and greater than 3 s, and then carry out the envelope of the maxima depends on Θ [1].

9. The calculation of inertial asymmetry coefficients for the realizations of the noise

The process of changing the temperature of additional heat is proportional to the quadratic inertial process ω2T(t) or the square of the coefficient of asymmetry given K2ωT(t). In this regard, it suffices to consider these processes under a single coefficient of proportionality c2ν. Since the time constants of heating can be arbitrary, for the calculations is to obtain T-characteristics: the dependence of the calculated maxima K2ωTmax of T. При c2ν = 1 this dependence is called the base.

Energy slow process at the output of the quadratic inertial smoothing (QSI) in a model of the EMC can be calculated using the Duhamel integral, which can be written as:

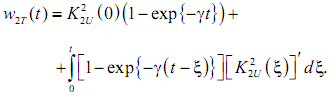
pic21
(1)

In computer calculations, it is more convenient to use the method of successive intervals. The assumption that within each interval Δ ordinate the initial schedule are unchanged, and accepted Duhamel integral. We obtain the coordinates

pic22
(2)

energy at the end of the process r-th stage. At t = 0 the initial ordinate ω2Tн1 first step is taken to be zero.

Schedule of squares of the asymmetry is shown in fig. 5, and a curve (as in fig. 3, a). Consistent application of the formula gives a curve 2. The desired graph (fig. 5, b) is obtained by taking the square root of the ordinate of the curve 2.

The transition process is almost complete in 3T, so to highlight the initial part of the stationary state is discarded (shaded area). Based on the remaining portion of the statistical distribution function F(K2ωT), which is presented in fig. 6 curve 1. Here, as in fig. 4, for comparison, curve 2 shows the distribution function of the original schedule. Through a horizontal 0,95 to its intersection with the curve 1, we obtain the required one-second maximum (bright circle). As shown in fig. 4, the maximum of the original schedule K2Umax (dark circle) [1].

Figure 5 – Construction of one-second schedule of the reduced coefficients of the inertial asymmetry of stress at work EAF-100

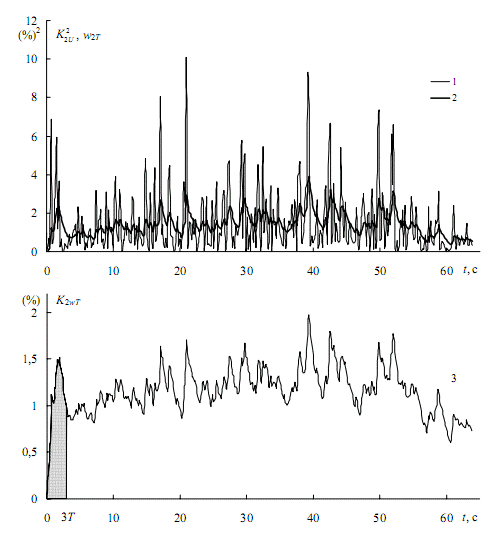
Figure 5 – Construction of one-second schedule of the reduced coefficients of the inertial asymmetry of stress at work EAF-100

Similarly, we calculated the inertial peaks for other values of the heating time constant, which gives T-characteristic shown in fig. 7. Its greatest value is achieved at zero. With an unlimited increase in the heating time constant highs tend to an effective value.

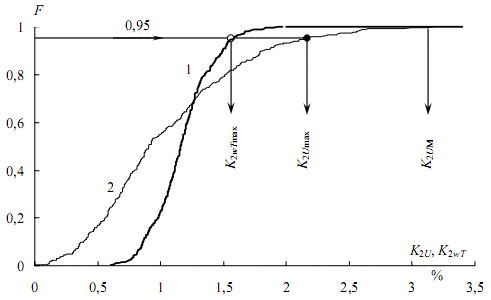
Figure 6 – The distribution function of voltage unbalance factors at work EAF-100: 1 – inertia (T = 1 s), 2 – source (T = 0)

Figure 6 – The distribution function of voltage unbalance factors at work EAF-100: 1 – inertia (T = 1 s), 2 – source (T = 0)

Figure 7 – Dependence of asymmetry coefficients of the given inertial stress from the constant heating time (at work EAF-100)

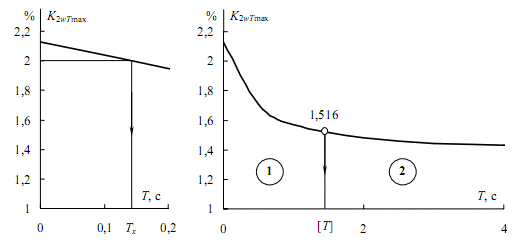
Figure 7 – Dependence of asymmetry coefficients of the given inertial stress from the constant heating time (at work EAF-100)

We find the minimum value Tmin at which the calculation is already possible to carry on the effective value of the relative error of – 10%. After a horizontal 1,1K2Uэ = 1,314% (in fig. 7 not shown) to the intersection with T-characteristic, we obtain the value 13 s. At T > 13 the error in calculating the effective value is less than 10%.

In cases where the maximum allowable temperature of the heat of the asymmetry is not set, its value is tentatively proposed to take from the conditions under which the norm [3] for the normal modes:

pic26
(3)

With this assumption, the estimation of temperature is equivalent to EMC evaluation of the inertial coefficients. Horizontal 2% cross T-characteristic in response to T = 0,155 and divides it into two parts: the left of the asymmetry of 0,155 according to [3] is unacceptable, and right – is admissible. This again emphasizes the need to consider the actual time constants of heating. Note that the use of (3) can significantly tighten or ease the requirements for EMC. For example, the electric motor allowable temperature is 7,5 °C, while the formula (3) gives only 2 °C. Accordingly, the permissible value of the asymmetry coefficient is 3,873, not 2%.

In fig. 7 open circles show the value of 1,516% cumulative three-second schedule. It corresponds to the constant heating time [T] = 1,61 s. If you have constant power-consuming equipment in a heat, the evaluation of asymmetry, according to [3] underestimates the claims, since the inertial peaks higher than 1,516%. In region 2, by contrast, claims overstated. It should be noted that the compliance rate of the inertial and cumulative maximum of 3/1,61 = 1,863, which is closer to the value of 2,25, but not to the 3 – as is customary in the theory of electrical loads.

This example confirms the incorrect use of standards [3] to estimate the EMC [1].


On the moment of writing this abstract the master's work was not completed. Final completion: December 2012. The full text of the work and materials on the topic be obtained from the author or the scientific adviser after that date.

References

  1. В.Г. Кузнецов, Э.Г. Куренный, А.П. Лютый Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения – Донецк: Норд – пресс, 2005. – 250 с.
  2. А.К. Шидловский, Б.П. Борисов, Г.Я. Вагин, Э.Г. Куренный, И.Г. Крахмалин Электромагнитгая совместимость электроприёмников промышленных предприятий – Киев: Наукова думка, 1992. – 236 с.
  3. ГОСТ 13109 – 97 Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения [Электронный ресурс]. – Режим доступа: http://rgost.ru/....
  4. А.К. Шидловский, Э.Г. Куренный Введение в статистическую динамику систем электроснабжения – Киев: Наукова думка, 1984. – 273 с.
  5. А.К. Шидловский, В.Г. Кузнецов Повышение качества энергии в электрических сетях – Киев: Наукова думка, 1985. – 268 с.
  6. Салтыков А.В. Электромагнитная совместимость параллельных дуговых сталеплавильных печей с системой электроснабжения – Диссертация кандидата технических наук, Самара, 2006 [Электронный ресурс]. – Режим доступа: http://www.dissercat.com/....
  7. А.А. Ермилов Основы электроснабжения промышленных предприятий – М.: Энергоатомиздат, 1983. – 208 с.
  8. И.В. Жежеленко, Ю.Л. Саенко Показатели качества электроэнергии и их контроль на промышленных предприятиях – М.: Энергоатомиздат, 2000. – 252 с.
  9. Э.Г. Куренный, Е.Н. Дмитриева, А.П. Лютый, О.А. Сидоренко Оценка и нормирование несимметрии напряжений в системах электроснабжения общего назначения – Электричество, 2008, №4. – с. 18-26.
  10. В.Г. Кузнецов, Е.Г. Курінний, О.П. Лютий Електромагнітна сумісність. Доза несиметрії напруги – Технічна електродинаміка, 2005, №3. – с. 49-53.