Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Практична та наукова актуальність теми
- 2. Мета та задачі
- 3. Поняття несиметрії напруг
- 4. Вихідні дані
- 5. Нормування несиметрії згідно ГОСТ 13109 – 97
- 6. Перевірка можливості розрахунку несиметрії по записам фазних і лінійних напруг
- 7. Нормовані показники ЕМС за несиметрією напруг
- 8. Розрахунок кумулятивних коефіцієнтів несиметрії за графіком перешкоди
- 9. Розрахунок інерційних коефіцієнтів несиметрії за реалізаціями перешкоди
- Список использованной литературы
Вступ
Електромагнітна сумісність (ЕМС) (electromagnetic compatibility – EMC) – це здатність технічного засобу ефективно функціонувати із заданою якістю в певній електромагнітної обстановці, не створюючи при цьому неприпустимих електромагнітних завад іншим технічним засобам. В даний час на промислових підприємствах спостерігається постійне зростання числа і потужності електроприймачів, що створюють різні електромагнітні перешкоди (ЕМП), які, поширюючись як в повітряному середовищі, так і по провідникам електричного струму, по-різному впливають на самі електроприймачі і на системи їх управління, захисту , ЕОМ і автоматику. [2].
Питання якості електроенергії (ЯЕ) отримали істотний розвиток у більшості аспектів цієї багатогранної проблеми. Її значимість, насамперед в економічному плані, стала очевидною як для виробників, так і для споживачів електроенергії (ЕЕ).
Так, в США – збитки, зумовлені зниженою якістю еектроенергіі, становлять кілька десятків мільярдів доларів на рік. Дослідження цієї проблеми, проведене в кінці 80-х років в СЕП підприємств колишнього СРСР, показало, що щорічний збиток в промисловості внаслідок низької ЯЕ складає близько 10 млрд.дол/рік, причому більше 10% збитків приходиться на його технологічну складову. У США збитки, пов'язані з порушенням надійності СЕП, досягають 25-30 млрд.дол. на рік, причому, на думку фахівців порушення надійності електропостачання в ряді випадків пов'язана зі зниженою ЯЕ [8].
Тому проблема забезпечення спільної роботи різних електроприймачів, тобто їх ЕМС, з кожним роком стає більш актуальною.
1. Практична та наукова актуальність теми
Практична актуальність полягає в розробці достовірної методики оцінки несиметрії при роботі дугової сталеплавильної печі (ДСП), тому що порушення ЕМС призводить до необгрунтованого збільшення капіталовкладень, а заниження &ndash до збитку від додаткових втрат електроенергії, зниження терміну служби електроустаткування, погіршення якості продукції. У зв'язку з цим високі вимоги пред'являються до обгрунтованості і точності методів оцінювання ЕМС як на стадії проектування, так і в експлуатації систем електропостачання. Збиток від порушення ЕМС в Україні становить 1 млрд. доларів на рік.
Так як в діючих мережах перешкоди представляють собою випадкові процеси, потрібна розробка спільних методів аналізу. Існуючі методи використовують статичні моделі, що відносяться до повільної зміни напруги, що не підходить для оцінки несиметрії при роботі ДСП, коли напруга змінюється швидко. Це завдання вирішується за допомогою динамічного моделювання наслідків впливу перешкоди на електрообладнання. Тому наукова актуальність роботи полягає в забезпеченні достовірності оцінок ЕМС.
2. Мета та задачі
Мета роботи – оцінка несиметрії за експериментальними записами миттєвих значень фазних напруг і струмів ДСП, отриманих за допомогою цифрового осцилографа РЕКОН.
В роботі повинні бути вирішені наступні задачі:
- Перевірка можливості розрахунку несиметрії по записах фазних і лінійних напруг;
- Побудова графіків напруги зворотної послідовності;
- Перевірка наявності нульової послідовності в трипровідних мережах за дослідними даними;
- Оцінка впливу несиметрії на трифазні асинхронні і синхронні електродвигуни (АД і СД);
- Перевірка виконання ГОСТ на діючому підприємстві.
3. Поняття несиметрії напруг
Несиметрія напруги є найбільш поширеною кондуктивною перешкодою ЕМС. У системах електропостачання промислових підприємств несиметрія напруг може бути викликана зовнішніми і внутрішніми причинами. Зовнішня несиметрія зумовлена, по-перше, тим, що генератори на електричних станціях не можуть створювати абсолютно симетричну систему напруг. По-друге, лінії і трансформатори мають розкид в опорах фаз і коефіцієнтах трансформації. По-третє, на сусідніх підприємствах можуть бути настільки потужні споживачі з несиметричним навантаженням (ДСП, однофазні печі, тягові підстанції та інші), що вони створюють несиметрію в районних електричних мережах, від яких живиться розглянуте підприємство. У проектуванні передбачається, що зовнішня несиметрія відсутня [1].
Джерелом внутрішньої несиметрії є трифазні електроприймачі з несиметричним навантаженням (ДСП, магнитногідравлічні установки для точного лиття та ін), а також однофазні електроприймачі.
В більшості публікацій оцінювання несиметричних режимів проводиться для окремих випадків незмінної несиметрії та періодичних спотвореннях кривої напруги. Проте в діючих мережах перешкоди представляють собою випадкові процеси, тобто несиметрія змінюється в часі. Наприклад, при роботі ДСП:
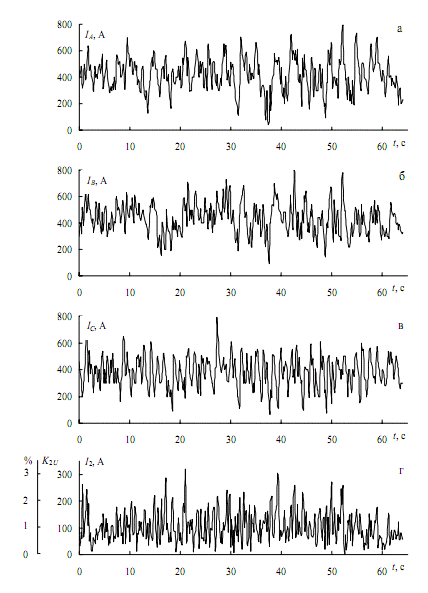
Рисунок 1 – Навантаження фаз (а-в) і струм зворотної послідовності (г) при роботі ДСП ємністю 100 т в період розплавлення
Тому оцінювання ЕМС по несиметрії вимагає розробки загальних методів аналізу.
Системи переміщення електродів в ДСП працюють незалежно один від одного, тому струми фаз не рівні між собою, що створює несиметрію напруг в мережі електропостачання. Несиметрія найбільше впливає на АД і СД. У стандарті нормуються трисекундні коефіцієнти несиметрії в точках загального приєднання, які використовуються в комерційних розрахунках за споживану електроенергію і виявлення джерел порушення ЕМС. Проте за ними не можна оцінити негативний вплив несиметрії на конкретні електроприймачі (на АД і СД). Для діючих підприємств необхідно мати графіки симетричних складових, які можуть бути отримані за експериментальними записами напруг [1].
4. Вихідні дані
Вихідними даними є графіки фазних напруг і струмів ДСП, отримані в період розплавлення (на початку, в середині і в кінці плавки). Запис здійснювався в одному з сталеплавильних цехів металургійного заводу за допомогою цифрового осцилографа РЕКОН. Тривалість запису склала 29 с., значення фіксувалися за кожні 0,0005 с, що склало 58000 значень для кожного параметру запису.
5. Нормування несиметрії згідно ГОСТ 13109 – 97
Згідно [3] несиметрія напруг характеризується наступними показниками:
- коефіцієнтом несиметрії напруг за зворотньою послідовністю;
- коефіцієнтом несиметрії напруг за нульовою послідовністю.
Спочатку визначають діюче значення напруги прямої, зворотної і нульової послідовності основної частоти за формулами:
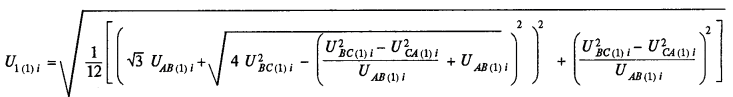
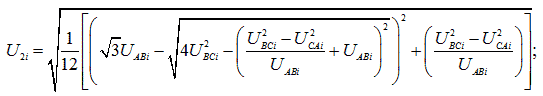
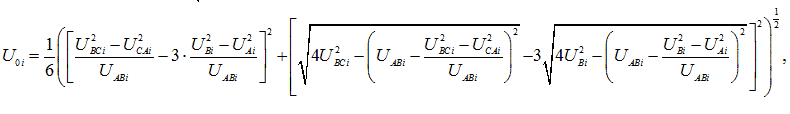
де UAB(1)i, UBC(1)i, UCA(1)i – діючі значення міжфазних напруг основної частоти в i-му спостереженні, В, кВ;
Коефіцієнт несиметрії напруг за зворотньою і нульовою послідовністю К2Ui и К0Ui обчислюють у відсотках як результат i-го спостереження за формулами:
де U2(1)i, U0(1)i – діюче значення напруги зворотньої та нульової послідовності основної частоти трифазної системи напруг в i-му спостереженні, В, кВ;
U1(1)i – діюче значення напруги прямої послідовності основної частоти в i-му спостереженні, В, кВ.
6. Перевірка можливості розрахунку несиметрії по записам фазних і лінійних напруг
В результаті досліду за допомогою цифрового регітратора РЕКОН записувалися фазні напруги. Виникає питання, чи можна розраховувати показники несиметрії за міжфазними (лінійними) напругами?
Розглянемо приклад, коли точка O нейтралі і O' навантаження збігаються (тобто навантаження не зміщує точку нейтралі).
Задамо значення амплітуди фазної напруги UA = 220 В, UB = 0,5·UA = 0,5·220 = 110 В, кут між векторами фазних напруг UA и UB приймаємо 120°.
Побудуємо векторну діаграму (ВД) фазних та лінійних напруг:

ВД фазних та лінійних напруг
Запишемо фазні напруги в комплексній формі:
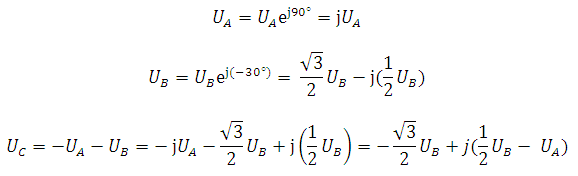
Вирази для міжфазних напруг:
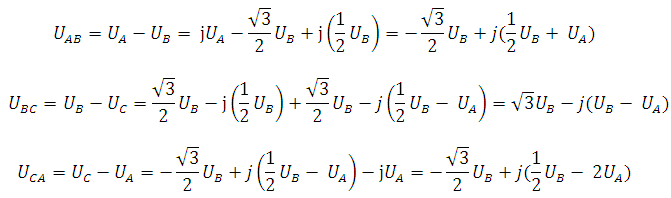
Після підстановки амплітуди фазної напруги UA = 220 В и UB = 0,5·UA = 0,5·220 = 110 В в записані вище вирази отримаємо:
| UC, В | UAB, В | UBC, В | UCA, В |
| 190,5256 | 291,0326 | 220 | 396,6106 |
Згідно [3] визначимо діючі значення напруг прямої U1 і зворотньої U2 послідовності за значеннями фазних і лінійних напруг:
| За фазними напругами | За лінійними напругами | ||
| U1, В | U2, В | U1, В | U2, В |
| 168,0278 | 63,50853 | 291,0326 | 110 |
Коефіцієнт несиметрії напруг за зворотньою послідовністю К2Ui:
- за записами фазних напруг:

- за лінійними напругами:

Отримані значення коефіцієнтів несиметрії напруг за зворотньою послідовністю збіглися, тому можна розраховувати показники несиметрії як по фазним так і лінійним напругам. Але якщо точка навантаження O' зміщена, то розрахунок за лінійними напругами не допускається.
7. Нормовані показники ЕМС за несиметрією напруг
Спочатку в стандартах різних країн нормувалися лише допустимі значення коефіцієнта несиметрії. Ці норми мають наочний сенс лише для окремого випадку незмінної несиметрії, коли в рамках статичної моделі за коефіцієнтом несиметрії можна однозначно визначити показники ЕМС. Наступним етапом стало введення норм і на короткочасні зміни несиметрії: рівень несиметрії встановлювався від 1 до 3%, а короткочасно допускалася несиметрія від 2 до 5%. Для СД вказувалася тривалість короткочасного підвищення несиметрії за 1 мін. З 1981 р. допустима несиметрія почала оцінюватися з інтегральною імовірністю 95%, тобто при нормуванні став використовуватися принцип практичної впевненості [1].
В [3] нормуються трисекундні середньоквадратичні величини коефіцієнтів несиметрії. У позначеннях не робиться відмінностей між поточними і усередненими значеннями: K2Ui – i-е поточне та К2U – осереднене, а також між вимірюваними (або розрахованими) і нормованими значеннями. Приймемо наступні позначення: [Θ] = 3 с – нормована тривалість кумуляції (в [3] – позначена через Tνs); K2U, K2ωΘ, K2ω[Θ] – поточні, кумулятивні і трисекундні приведені коефіцієнти несиметрії.
В [3] прийнято дискретне осереднення на прилеглих один до одного трисекундних інтервалах. У кожному інтервалі береться N ординат – не менше 9. Крок дискретизації буде дорівнювати 3/(N + 1) – не більше 0,3 с, якщо в N не враховувати кінцеву або початкову ординату. Кумулятивний коефіцієнт несиметрії:
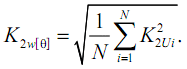
Так як контроль несиметрії здійснюється за добу, кількість трисекундних інтервалів велика, тому за умови стаціонарності процесу дискретне осереднення дає той же результат, що і безперервне:
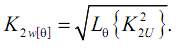
Розрахункові максимальні значення K2[Θ]н max і K2[Θ]п max для нормального і граничного режимів, визначені з граничними імовірностями 0,05 і 0,001, не повинні перевищувати відповідні допустимі значення ([] в позначеннях):
які в [3] прийняті рівними 2 та 4% [1].
Формально перетворенню (2) відповідає деякий кумулятивний
стандартний електроприймач. Відсутність множника перед сумою в (1) означає, що в модель ЕМС (рис. 2, а) немає необхідності вводити зважуючий фільтр (ЗФ) – його коефіцієнт передачі дорівнює одиниці. Квадратор 1 і кумулятивна ланка 3 формують квадратичний кумулятивний процес:
Блок обчислення показників ЕМС (ПЕ) включає до себе ланку 7 вилучення квадратного кореня і блок 8 визначення розрахункових максимальних значень із заданою граничною імовірністю [1].

Рисунок 2 – Структурні схеми моделей стандартних електроприймачів за несиметрією напруг: а – кумулятивного, б – інерційного
8. Розрахунок кумулятивних коефіцієнтів несиметрії за графіком перешкоди
Приведені кумулятивні коефіцієнти несиметрії напруг K2ωΘ тривалістю [Θ] = 3 с розраховуються для перевірки виконання норм стандарту [3]. Розрахунок не вимагається лише у двох випадках. По-перше, якщо найбільше значення K2UM не перевищує 2%, вимоги стандарту завідомо виконуються. По-друге, оскільки трисекундний кумулятивний максимум не може бути більше ефективного значення коефіцієнта несиметрії, то при
вимоги стандарту безумовно порушуються [1].
Перед розрахунком за заданим графіком коефіцієнтів несиметрії доцільно перевірити виконання умови:
Якщо воно не порушується, то замість квадратичного кумулятивного осереднення достатньо виконати трисекундне осереднення вихідного графіка, а не його квадрата.
Осереднення виконується в такій послідовності. Вихідний графік зводиться в квадрат (рис. 3, крива 1). При Θ = 0 інтервал осереднення розташовується зліва від осі ординат, не захоплюючи графік. Тому осереднене на інтервалі значення дорівнює нулю – воно відноситься до кінця інтервалу, тобто до t = 0. Потім інтервал осереднення зсувається на крок Δ вправо, захоплюючи початкову ординату K22U(0). Осереднене значення Δ·K22U(0)/[Θ] належить до моменту t = Δ. Інтервал знову зсувається на крок Δ, і т.д. Отриманий енергетичний кумулятивний процес ω2Θ[t] представлений на рис. 3 кривою 2. Витягуючи з ординат цього графіка квадратний корінь, одержимо шуканий процес (крива 3) [1].
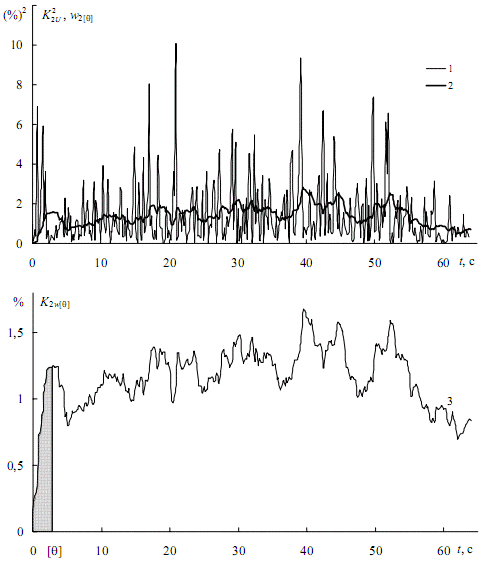
Рисунок 3 – До визначення трисекундного кумулятивного графіку коефіцієнтів несиметрії напруг при роботі ДСП-100
На початковій ділянці протікає випадковий перехідний процес. З рис. 3 (ламана 1) випливає, що цей процес повністю закінчується рівно через 3 с. Відкинувши ділянку графіка від 0 до 3 с (затушована область), отримаємо графік стаціонарного режиму. Для нього обчислимо ефективне значення K2[Θ]э і стандарт σ2[Θ], а також побудуємо функцію розподілу F(K2ω[Θ]), представлену на рис. 4 кривою 1. Тут же для порівняння показана функція розподілу вихідного графіка (крива 2). Так як осереднення згладжує графік, то крива 1 менш полога, ніж крива 2 [1].
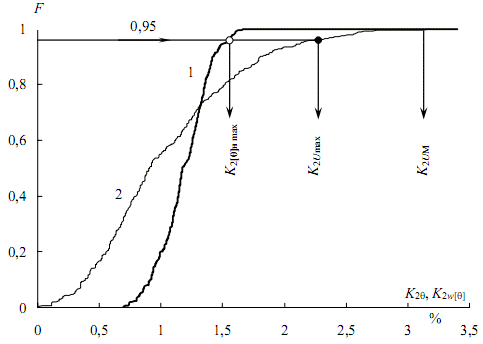
Рисунок 4 – Функція розподілу коефіцієнтів несиметрії напруг при роботі ДСП-100: 1 – трисекундних, 2 – вихідних
Для визначення максимального розрахункового значення коефіцієнта несиметрії в нормальному режимі K2[Θ]н max проведемо горизонталь 0,95 до перетину з графіком функції розподілу (світлий кружок). Якщо це значення менше 2–%, то вимога стандарту не порушується. Розрахунковий максимум вихідного графіка K2Umax (темний кружок) більше трисекундного. Це свідчить про те, що оцінювати допустимість несиметрії в рамках статичної моделі, без осереднення, неприпустимо.
Перевірку по виконанню норм для граничного режиму не виробляємо, тому що найбільша ордината вихідного графіка не перевищує 4%.
Кореляційна функція коефіцієнтів несиметрії не містить періодичної складової, тому немає необхідності розраховувати кумулятивні максимуми для значень Θ менше і більше 3 с, а потім проводити огинаючу залежності максимумів від Θ [1].
9. Розрахунок інерційних коефіцієнтів несиметрії за реалізаціями перешкоди
Процес зміни температури додаткового перегріву пропорційний квадратичному інерційному процесу ω2T(t) або квадратам приведеного коефіцієнту несиметрії K2ωT(t). У зв'язку з цим досить розглянути ці процеси при одиничному коефіцієнті пропорційності c2ν. Так як постійні часу нагріву можуть бути будь-якими, метою розрахунків є отримання T-характеристики: залежність розрахункових максимумів K2ωTmax від Т. При c2ν = 1 таку залежність будемо називати базовою.
Енергетичний інерційний процес на виході блоку квадратичного інерційного згладжування (КЗІ) в моделі ЕМС може бути розрахований за допомогою інтеграла Дюамеля, який записується у вигляді:
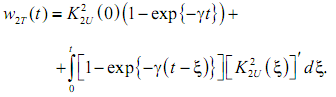
У комп'ютерних розрахунках зручніше використовувати метод послідовних інтервалів. Припущення про те, що в межах кожного інтервалу Δ ординати вихідного графіка незмінні, прийнято і в інтегралі Дюамеля. Отримаємо ординати
енергетичного процесу в кінці r-го ступеня. При t = 0 початкова ордината ω2Tн1 першого ступеня приймається рівною нулю.
Графік квадратів коефіцієнтів несиметрії представлений на рис. 5, а кривою 1 (як і на рис. 3, а). Послідовне застосування формули дає криву 2. Шуканий графік (рис. 5, б) виходить витяганням квадратного кореня з ординат кривої 2.
Перехідний процес практично закінчується через ЗТ, тому для виділення стаціонарного стану початкова ділянка відкидається (затушована область). За ділянкою що залишилася будується статистична функція розподілу F(K2ωT), яка представлена на рис. 6 кривою 1. Тут же, як і на рис. 4, для порівняння приведена крива 2 функції розподілу вихідного графіка. Проводячи горизонталь 0,95 до перетину з кривою 1, отримаємо шуканий односекундний максимум (світлий кружок). Як і на рис. 4, максимум вихідного графіка K2Umax (темний кружок) [1].
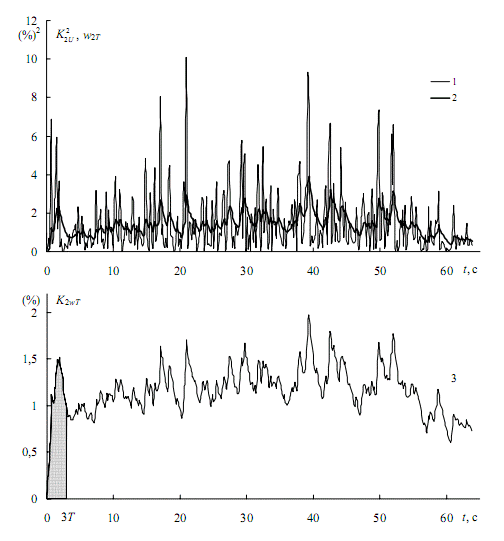
Рисунок 5 – До побудови односекундного інерційного графіка приведених коефіцієнтів несиметрії напруг при роботі ДСП-100
Аналогічним чином були розраховані інерційні максимуми для інших значень постійної часу нагріву, що дозволяє отримати T-характеристику, представлену на рис. 7. Найбільше її значення досягається в нулі. При необмеженому збільшенні постійної часу нагріву максимуми прагнуть до ефективного значення.
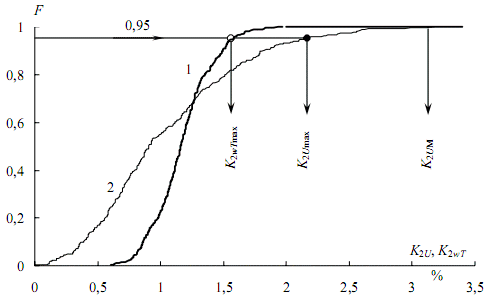
Рисунок 6 – Функція розподілу коефіцієнтів несиметрії напруг при роботі ДСП-100: 1 – інерційних (Т = 1 с), 2 – вихідних (Т = 0)
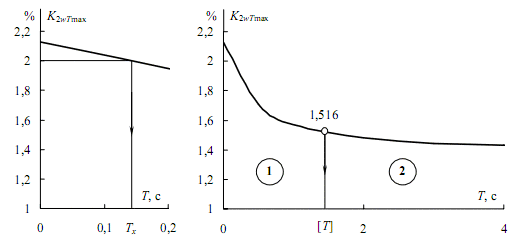
Рисунок 7 – Залежності приведених інерційних коефіцієнтів несиметрії напруг від постійної часу нагріву (при роботі ДСП-100)
Знайдемо мінімальне значення Tmin при якому розрахунок вже можна виконувати за ефективним значенням з відносною похибкою – 10%. Провівши горизонталь 1,1K2Uэ = 1,314% (на рис. 7 не показана) до перетину з Т-характеристикою, отримаємо значення 13 с. При Т > 13 с похибка розрахунку за ефективним значенням буде менше 10%.
У тих випадках, коли допустима максимальна температура перегріву від несиметрії не задана, її значення орієнтовно пропонується приймати за умови виконання норми [3] для нормального режиму:
При такому припущенні оцінювання ЕМС за температурою рівноцінно оцінюванню за інерційними коефіцієнтами. Горизонталь 2% перетинає T-характеристику при Тх = 0,155 с і поділяє її на дві частини: ліворуч від 0,155 несиметрія згідно [3] недопустима, а праворуч – допустима. Це ще раз підкреслює необхідність врахування фактичних постійних часу нагріву. Відзначимо, що використання співвідношення (3) може істотно посилити або пом'якшити вимоги до ЕМС. Наприклад, для електродвигунів допустима температура дорівнює 7,5 °С, у той час як формула (3) дає всього 2 °С. Відповідно допустиме значення коефіцієнта несиметрії становить 3,873, а не 2%.
На рис. 7 світлим кружком показано значення 1,516% трисекундного кумулятивного графіку. Йому відповідає постійна часу нагріву [T] = 1,61 с. Якщо електроприймачі мають постійні нагріву в області 1, то оцінювання несиметрії згідно [3] занижує вимоги, так як інерційні максимуми перевищують 1,516%. В області 2, навпаки, вимоги завищуються. Слід зазначити, що коефіцієнт відповідності інерційного і кумулятивного максимуму становить 3/1, 61 = 1,863, що ближче до значення 2,25, але не до 3 – як прийнято в теорії електричних навантажень.
Розглянутий приклад підтверджує некоректність використання норм [3] для оцінювання ЕМС [1].
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.
Список використаної літератури
- В.Г. Кузнецов, Э.Г. Куренный, А.П. Лютый Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения – Донецк:
Норд – пресс
, 2005. – 250 с. - А.К. Шидловский, Б.П. Борисов, Г.Я. Вагин, Э.Г. Куренный, И.Г. Крахмалин Электромагнитгая совместимость электроприёмников промышленных предприятий – Киев:
Наукова думка
, 1992. – 236 с. - ГОСТ 13109 – 97 Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения [Электронный ресурс]. – Режим доступа: http://rgost.ru/....
- А.К. Шидловский, Э.Г. Куренный Введение в статистическую динамику систем электроснабжения – Киев:
Наукова думка
, 1984. – 273 с. - А.К. Шидловский, В.Г. Кузнецов Повышение качества энергии в электрических сетях – Киев:
Наукова думка
, 1985. – 268 с. - Салтыков А.В. Электромагнитная совместимость параллельных дуговых сталеплавильных печей с системой электроснабжения – Диссертация кандидата технических наук, Самара, 2006 [Электронный ресурс]. – Режим доступа: http://www.dissercat.com/....
- А.А. Ермилов Основы электроснабжения промышленных предприятий – М.: Энергоатомиздат, 1983. – 208 с.
- И.В. Жежеленко, Ю.Л. Саенко Показатели качества электроэнергии и их контроль на промышленных предприятиях – М.: Энергоатомиздат, 2000. – 252 с.
- Э.Г. Куренный, Е.Н. Дмитриева, А.П. Лютый, О.А. Сидоренко Оценка и нормирование несимметрии напряжений в системах электроснабжения общего назначения – Электричество, 2008, №4. – с. 18-26.
- В.Г. Кузнецов, Е.Г. Курінний, О.П. Лютий Електромагнітна сумісність. Доза несиметрії напруги – Технічна електродинаміка, 2005, №3. – с. 49-53.
