Реферат по теме выпускной работы
Содержание
- Введение
- 1. Практическая и научная актуальность темы
- 2. Цели и задачи
- 3. Понятие несимметрии напряжений
- 4. Исходные данные
- 5. Нормирование несимметрии согласно ГОСТ 13109 – 97
- 6. Проверка возможности расчёта несимметрии по записям фазных и линейных напряжений
- 7. Нормируемые показатели ЭМС по несимметрии напряжений
- 8. Расчет кумулятивных коэффициентов несимметрии по графику помехи
- 9. Расчет инерционных коэффициентов несимметрии по реализациям помехи
- Список использованной литературы
Введение
Электромагнитная совместимость (ЭМС) (electromagnetic compatibility – EMC) – это способность технического средства эффективно функционировать с заданным качеством в определенной электромагнитной обстановке, не создавая при этом недопустимых электромагнитных помех другим техническим средствам. В настоящее время на промышленных предприятиях наблюдается постоянный рост числа и мощности электроприемников, создающих различные электромагнитные помехи (ЭМП), которые, распространяясь как в воздушной среде, так и по проводникам электрического тока, оказывают различные влияния на сами электроприемники и на системы их управления, защиты, ЭВМ и автоматику [2].
Вопросы качества электроэнергии (КЭ) получили существенное развитие в большинстве аспектов этой многогранной проблемы. Ее значимость, прежде всего в экономическом плане, стала очевидной как для производителей, так и для потребителей электроэнергии (ЭЭ).
Так, в США – убытки, обусловленные пониженным качеством эектроэнергии, составляют несколько десятков миллиардов долларов в год. Исследование этой проблемы, проведенное в конце 80-х годов в СЭС предприятий бывшего СССР, показало, что ежегодный ущерб в промышленности вследствие низкого КЭ составляет около 10 млрд.дол/год, причем более 10% ущерба приходится на его технологическую составляющую. В США убытки, связанные с нарушением надежности СЭС, достигают 25 – 30 млрд.дол. в год, причем, по мнению специалистов нарушение надёжности электроснабжения в ряде случаев связано с пониженным КЭ [8].
Поэтому проблема обеспечения совместной работы различных электроприемников, т.е. их ЭМС, с каждым годом становится более актуальной.
1. Практическая и научная актуальность темы
Практическая актуальность заключается в разработке достоверной методики оценки несимметрии при работе дуговой сталеплавильной печи (ДСП), т.к. нарушение ЭМС приводит к необоснованному увеличению капиталовложений, а занижение – к ущербу от дополнительных потерь электроэнергии, снижения срока службы электрооборудования, ухудшения качества продукции. В связи с этим высокие требования предъявляются к обоснованности и точности методов оценивания ЭМС как на стадии проектирования, так и в эксплуатации систем электроснабжения. Ущерб от нарушения ЭМС в Украине составляет 1 млрд. долларов в год.
Так как в действующих сетях помехи представляют собой случайные процессы, требуется разработка общих методов анализа. Существующие методы используют статические модели, относящиеся к медленному изменению напряжения, что не подходит для оценки несимметрии при работе ДСП, когда напряжение изменяется быстро. Эта задача решается с помощью динамического моделирования последствий воздействия помехи на электрооборудование. Поэтому научная актуальность работы заключается в обеспечении достоверности оценок ЭМС.
2. Цели и задачи
Цель работы – оценка несимметрии по экспериментальным записям мгновенных значений фазных напряжений и токов ДСП, полученных с помощью цифрового осциллографа РЕКОН.
В работе должны быть решены следующие задачи:
- Проверка возможности расчёта несимметрии по записям фазных и линейных напряжений;
- Построение графиков напряжения обратной последовательности;
- Проверка наличия нулевой последовательности в трёхпроводных сетях по опытным данным;
- Оценка влияния несимметрии на трёхфазные асинхронные и синхронные электродвигатели (АД и СД);
- Проверка выполнения ГОСТ на действующем предприятии.
3. Понятие несимметрии напряжений
Несимметрия напряжения является наиболее распространённой кондуктивной помехой ЭМС. В системах электроснабжения промышленных предприятий несимметрия напряжений может быть вызвана внешними и внутренними причинами. Внешняя несимметрия обусловлена, во-первых, тем, что генераторы на электрических станциях не могут создавать абсолютно симметричную систему напряжений. Во-вторых, линии и трансформаторы имеют разброс в сопротивлениях фаз и коэффициентах трансформации. В-третьих, на соседних предприятиях могут быть настолько мощные потребители с несимметричной нагрузкой (ДСП, однофазные печи, тяговые подстанции и др.), что они создают несимметрию в районных электрических сетях, от которых питается рассматриваемое предприятие. В проектировании предполагается, что внешняя несимметрия отсутствует [1].
Источником внутренней несимметрии являются трехфазные электроприемники с несимметричной нагрузкой (ДСП, магнитногидравлические установки для точного литья и др.), а также однофазные электроприемники.
В большинстве публикаций оценивание несимметричных режимов производится для частных случаев неизменной несимметрии и периодических искажениях кривой напряжения. Однако в действующих сетях помехи представляют собой случайные процессы, т.е. несимметрия изменяется во времени. Например, при работе ДСП:
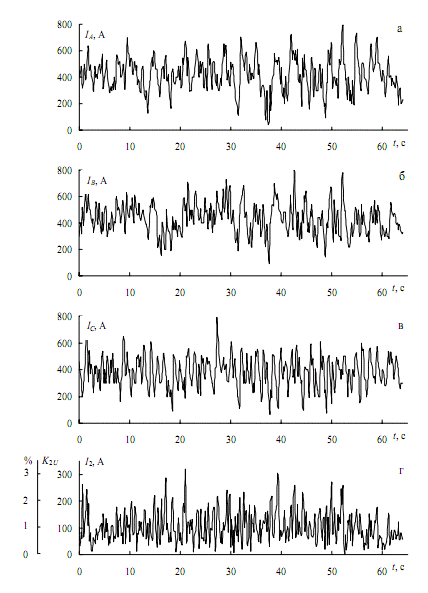
Рисунок 1 – Нагрузки фаз (а-в) и ток обратной последовательности (г) при работе ДСП ёмкостью 100 т в период расплавления
Поэтому оценивание ЭМС по несимметрии требует разработки общих методов анализа.
Системы перемещения электродов в ДСП работают независимо друг от друга, поэтому токи фаз не равны между собой, что создаёт несимметрию напряжений в сети электроснабжения. Несимметрия больше всего сказывается на АД и СД. В стандарте нормируются трёхсекундные коэффициенты несимметрии в точках общего присоединения, которые используются в коммерческих расчётах за потребляемую электроэнергию и выявления источников нарушения ЭМС. Однако по ним нельзя оценить негативное влияние несимметрии на конкретные электроприёмники (на АД и СД). Для действующих предприятий необходимо иметь графики симметричных составляющих, которые могут быть получены по экспериментальным записям напряжений [1].
4. Исходные данные
Исходными данными являются графики фазных напряжений и токов ДСП, полученные в период расплавления (в начале, в середине и в конце плавки). Запись осуществлялась в одном из сталеплавильных цехов металлургического завода с помощью цифрового осциллографа РЕКОН. Длительность записи составила 29 с., значения фиксировались за каждые 0,0005 с, что составило 58000 значений для каждого параметра записи.
5. Нормирование несимметрии согласно ГОСТ 13109 – 97
Согласно [3] несимметрия напряжений характеризуется следующими показателями:
- коэффициентом несимметрии напряжений по обратной последовательности;
- коэффициентом несимметрии напряжений по нулевой последовательности.
Вначале определяют действующее значение напряжения прямой, обратной и нулевой последовательности основной частоты по формулам:
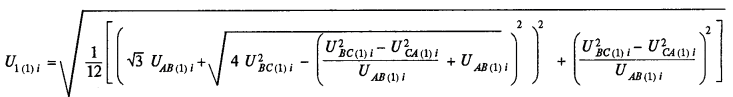
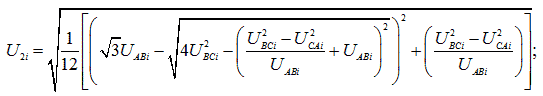
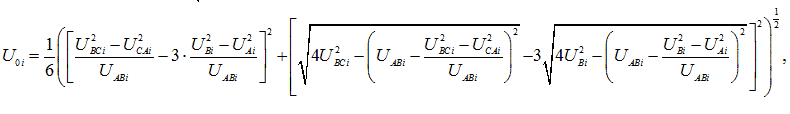
где UAB(1)i, UBC(1)i, UCA(1)i – действующие значения междуфазных напряжений основной частоты в i-ом наблюдении, В, кВ;
Коэффициент несимметрии напряжений по обратной и нулевой последовательностям К2Ui и К0Ui вычисляют в процентах как результат i-го наблюдения по формулам:
где U2(1)i, U0(1)i – действующее значение напряжения обратной и нулевой последовательности основной частоты трехфазной системы напряжений в i-ом наблюдении, В, кВ;
U1(1)i – действующее значение напряжения прямой последовательности основной частоты в i-ом наблюдении, В, кВ.
6. Проверка возможности расчёта несимметрии по записям фазных и линейных напряжений
В результате опыта с помощью цифрового регистратора РЕКОН записывались фазные напряжения. Возникает вопрос, можно ли считать показатели несимметрии по междуфазным (линейным) напряжениям?
Рассмотрим пример, когда точка O нейтрали и O' нагрузки совпадают (т.е. нагрузка не смещает точку нейтрали).
Зададим значение амплитуды фазного напряжения UA = 220 В, UB = 0,5·UA = 0,5·220 = 110 В, угол между векторами фазных напряжений UA и UB принимаем 120°.
Построим векторную диаграмму (ВД) фазных и линейных напряжений:

ВД фазных и линейных напряжений
Запишем фазные напряжения в комплексной форме:
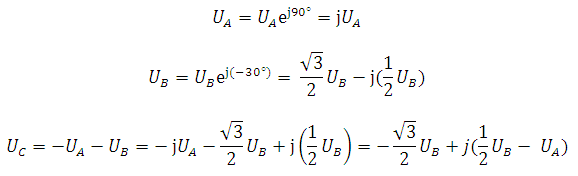
Выражения для междуфазных напряжений:
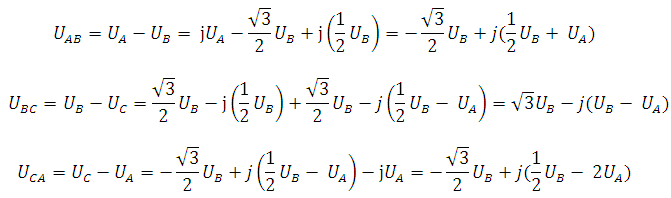
После подстановки амплитуды фазного напряжения UA = 220 В и UB = 0,5·UA = 0,5·220 = 110 В в записанные выше выражения получим:
| UC, В | UAB, В | UBC, В | UCA, В |
| 190,5256 | 291,0326 | 220 | 396,6106 |
Согласно [3] определим действующие значения напряжений прямой U1 и обратной U2 последовательностей по значениям фазных и линейных напряжений:
| По фазным напряжениям | По линейным напряжениям | ||
| U1, В | U2, В | U1, В | U2, В |
| 168,0278 | 63,50853 | 291,0326 | 110 |
Коэффициент несимметрии напряжений по обратной последовательности К2Ui:
- по записям фазных напряжений:

- по линейным напряжениям:

Полученные значения коэффициентов несимметрии напряжений по обратной последовательности совпали, значит можно считать показатели несимметрии как по фазным так и линейным напряжениям. Но если точка нагрузки O' смещена, то расчёт по линейным напряжениям не допускается.
7. Нормируемые показатели ЭМС по несимметрии напряжений
Первоначально в стандартах различных стран нормировались лишь допустимые значения коэффициента несимметрии. Эти нормы имеют наглядный смысл лишь для частного случая неизменной несимметрии, когда в рамках статической модели по коэффициенту несимметрии можно однозначно определить показатели ЭМС. Следующим этапом стало введение норм и на кратковременные изменения несимметрии: уровень несимметрии устанавливался от 1 до 3 %, а кратковременно допускалась несимметрия от 2 до 5%. Для СД указывалась длительность кратковременного повышения несимметрии за 1 мин. С 1981 г. допустимая несимметрия начала оцениваться с интегральной вероятностью 95%, т.е. при нормировании стал использоваться принцип практической уверенности [1].
В [3] нормируются трехсекундные среднеквадратичные величины коэффициентов несимметрии. В обозначениях не делается различий между текущими и осредненными значениями: K2Ui – i-е текущее и К2U – осредненное, а также между измеряемыми (или рассчитываемыми) и нормируемыми значениями. Примем следующие обозначения: [Θ] = 3 с – нормируемая длительность кумуляции (в [3] – обозначена через Tνs); K2U, K2ωΘ, K2ω[Θ] – текущие, кумулятивные и трехсекундные приведенные коэффициенты несимметрии.
В [3] принято дискретное осреднение на примыкающих друг к другу трехсекундных интервалах. В каждом интервале берется N ординат – не менее 9. Шаг дискретизации будет равен 3/(N + 1) – не более 0,3 с, если в N не учитывать конечную или начальную ординату. Кумулятивный коэффициент несимметрии:
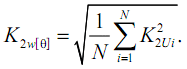
Так как контроль несимметрии осуществляется за сутки, количество трехсекундных интервалов велико, поэтому при условии стационарности процесса дискретное осреднение дает тот же результат, что и непрерывное:
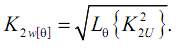
Расчетные максимальные значения K2[Θ]н max и K2[Θ]п max для нормального и предельного режимов, определенные с граничными вероятностями 0,05 и 0,001, не должны превышать соответствующие допустимые значения ([] в обозначениях):
которые в [3] приняты равными 2 и 4% [1].
Формально преобразованию (2) соответствует некоторой кумулятивный
стандартный электроприемник. Отсутствие множителя перед суммой в (1) означает, что в модель ЭМС (рис. 2, а) нет необходимости вводить взвешивающий фильтр (ВФ) – его коэффициент передачи равен единице. Квадратор 1 и кумулятивное звено 3 формируют квадратичный кумулятивный процесс:
Блок вычисления показателей ЭМС (ПЭ) включает в себя звено 7 извлечения квадратного корня и блок 8 определения расчетных максимальных значений с заданной граничной вероятностью [1].

Рисунок 2 – Структурные схемы моделей стандартных электроприемников по несимметрии напряжений: а – кумулятивного, б – инерционного
8. Расчет кумулятивных коэффициентов несимметрии по графику помехи
Приведенные кумулятивные коэффициенты несимметрии напряжений K2ωΘ длительностью [Θ] = 3 с рассчитываются для проверки выполнения норм стандарта [3]. Расчет не требуется лишь в двух случаях. Во-первых, если наибольшее значение K2UM не превышает 2%, требования стандарта заведомо выполняются. Во-вторых, поскольку трехсекундный кумулятивный максимум не может быть больше эффективного значения коэффициента несимметрии, то при
требования стандарта безусловно нарушаются [1].
Перед расчетом по заданному графику коэффициентов несимметрии целесообразно проверить выполнение условия:
Если оно не нарушается, то вместо квадратичного кумулятивного осреднения достаточно выполнить трехсекундное осреднение исходного графика, а не его квадрата.
Осреднение выполняется в следующей последовательности. Исходный график возводится в квадрат (рис. 3, кривая 1). При Θ = 0 интервал осреднения располагается слева от оси ординат, не захватывая график. Поэтому осредненное на интервале значение равно нулю – оно относится к концу интервала, т.е. к t = 0. Затем интервал осреднения сдвигается на шаг Δ вправо, захватывая начальную ординату K22U(0). Усредненное значение Δ·K22U(0)/[Θ] относится к моменту t = Δ. Интервал снова сдвигается на шаг Δ, и т.д. Полученный энергетический кумулятивный процесс ω2Θ[t] представлен на рис. 3 кривой 2. Извлекая из ординат этого графика квадратный корень, получим искомый процесс (кривая 3) [1].
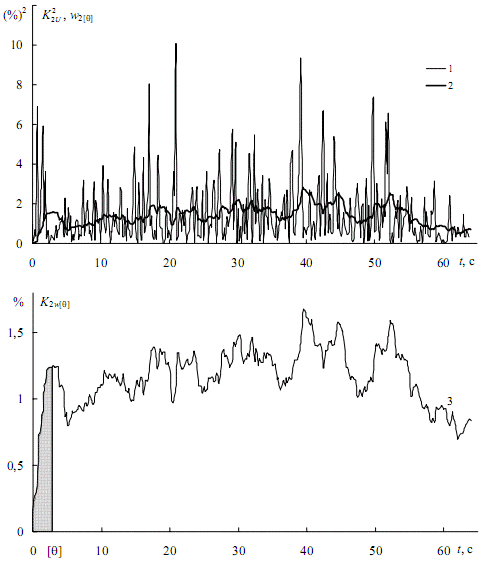
Рисунок 3 – К определению трехсекундного кумулятивного графика коэффициентов несимметрии напряжений при работе ДСП-100
На начальном участке протекает случайный переходный процесс. Из рис. 3 (ломаная 1) следует, что этот процесс полностью заканчивается ровно через 3 с. Отбросив участок графика от 0 до 3 с (затушеванная область), получим график стационарного режима. Для него вычислим эффективное значение K2[Θ]э и стандарт σ2[Θ], а также построим функцию распределения F(K2ω[Θ]), представленную на рис. 4 кривой 1. Здесь же для сравнения показана функция распределения исходного графика (кривая 2). Так как осреднение сглаживает график, то кривая 1 менее пологая, чем кривая 2 [1].
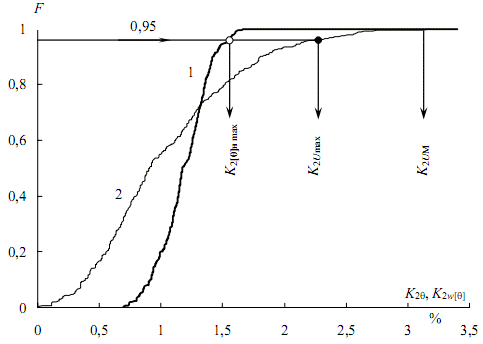
Рисунок 4 – Функция распределения коэффициентов несимметрии напряжений при работе ДСП-100: 1 – трехсекундных, 2 – исходных
Для определения максимального расчетного значения коэффициента несимметрии в нормальном режиме K2[Θ]н max проведем горизонталь 0,95 до пересечения с графиком функции распределения (светлый кружок). Если это значение меньше 2%, то требование стандарта не нарушается. Расчетный максимум исходного графика K2Umax (темный кружок) больше трехсекундного. Это свидетельствует о том, что оценивать допустимость несимметрии в рамках статической модели, без осреднения, недопустимо.
Проверку по выполнению норм для предельного режима не производим, так как наибольшая ордината исходного графика не превышает 4%.
Корреляционная функция коэффициентов несимметрии не содержит периодической составляющей, поэтому нет необходимости рассчитывать кумулятивные максимумы для значений Θ меньше и больше 3 с, а затем проводить огибающую зависимости максимумов от Θ [1].
9. Расчет инерционных коэффициентов несимметрии по реализациям помехи
Процесс изменения температуры дополнительного перегрева пропорционален квадратичному инерционному процессу ω2T(t) или квадратам приведенного коэффициента несимметрии K2ωT(t). В связи с этим достаточно рассмотреть эти процессы при единичном коэффициенте пропорциональности c2ν. Так как постоянные времени нагрева могут быть любыми, целью расчетов является получение T-характеристики: зависимость расчетных максимумов K2ωTmax от Т. При c2ν = 1 такую зависимость будем называть базовой.
Энергетический инерционный процесс на выходе блока квадратичного инерционного сглаживания (КСИ) в модели ЭМС может быть рассчитан с помощью интеграла Дюамеля, который записывается в виде:
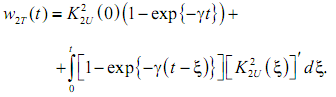
В компьютерных расчетах удобнее использовать метод последовательных интервалов. Предположение о том, что в пределах каждого интервала Δ ординаты исходного графика неизменны, принято и в интеграле Дюамеля. Получим ординаты
энергетического процесса в конце r-ой ступени. При t = 0 начальная ордината ω2Tн1 первой ступени принимается равной нулю.
График квадратов коэффициентов несимметрии представлен на рис. 5, а кривой 1 (как и на рис. 3, а). Последовательное применение формулы дает кривую 2. Искомый график (рис. 5, б) получается извлечением квадратного корня из ординат кривой 2.
Переходный процесс практически заканчивается через ЗТ, поэтому для выделения стационарного состояния начальный участок отбрасывается (затушеванная область). По оставшемуся участку строится статистическая функция распределения F(K2ωT), которая представлена на рис. 6 кривой 1. Здесь же, как и на рис. 4, для сравнения приведена кривая 2 функции распределения исходного графика. Проводя горизонталь 0,95 до пересечения с кривой 1, получим искомый односекундный максимум (светлый кружок). Как и на рис. 4, максимум исходного графика K2Umax (темный кружок) [1].
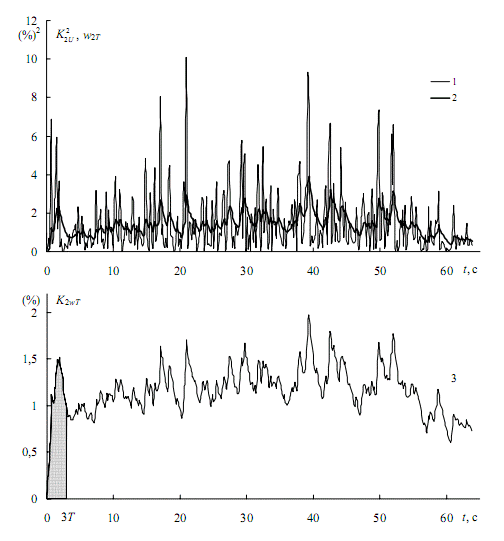
Рисунок 5 – К построению односекундного инерционного графика приведенных коэффициентов несимметрии напряжений при работе ДСП-100
Аналогичным образом были рассчитаны инерционные максимумы для других значений постоянной времени нагрева, что позволяет получить T-характеристику, представленную на рис. 7. Наибольшее ее значение достигается в нуле. При неограниченном увеличении постоянной времени нагрева максимумы стремятся к эффективному значению.
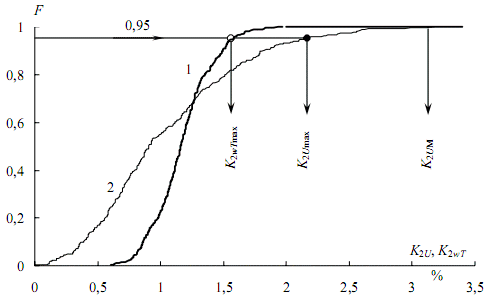
Рисунок 6 – Функция распределения коэффициентов несимметрии напряжений при работе ДСП-100: 1 – инерционных (Т = 1 с), 2 – исходных (Т = 0)
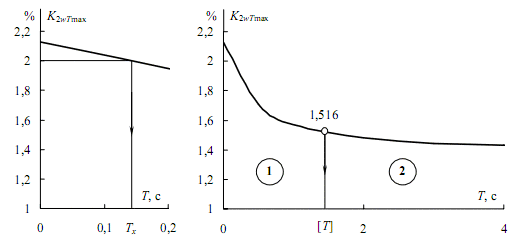
Рисунок 7 – Зависимости приведенных инерционных коэффициентов несимметрии напряжений от постоянной времени нагрева (при работе ДСП-100)
Найдем минимальное значение Tmin при котором расчет уже можно выполнять по эффективному значению с относительной погрешностью – 10%. Проведя горизонталь 1,1K2Uэ = 1,314% (на рис. 7 не показана) до пересечения с Т-характеристикой, получим значение 13 с. При Т > 13 с погрешность расчета по эффективному значению будет меньше 10%.
В тех случаях, когда допустимая максимальная температура перегрева от несимметрии не задана, ее значение ориентировочно предлагается принимать из условия выполнения нормы [3] для нормального режима:
При таком допущении оценивание ЭМС по температуре равноценно оцениванию по инерционным коэффициентам. Горизонталь 2% пересекает T-характеристику при Тх = 0,155 с и разделяет ее на две части: слева от 0,155 несимметрия согласно [3] недопустима, а справа – допустима. Это еще раз подчеркивает необходимость учета фактических постоянных времени нагрева. Отметим, что использование соотношения (3) может существенно ужесточить или смягчить требования к ЭМС. Например, для электродвигателей допустимая температура равна 7,5 °С, в то время как формула (3) дает всего 2 °С. Соответственно допустимое значение коэффициента несимметрии составляет 3,873, а не 2%.
На рис. 7 светлым кружком показано значение 1,516% трехсекундного кумулятивного графика. Ему соответствует постоянная времени нагрева [T] = 1,61 с. Если электроприемники имеют постоянные нагрева в области 1, то оценивание несимметрии согласно [3] занижает требования, так как инерционные максимумы превышают 1,516%. В области 2, напротив, требования завышаются. Следует отметить, что коэффициент соответствия инерционного и кумулятивного максимума составляет 3/1,61 = 1,863, что ближе к значению 2,25, но не к 3 – как принято в теории электрических нагрузок.
Рассмотренный пример подтверждает некорректность использования норм [3] для оценивания ЭМС [1].
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2012 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список использованной литературы
- В.Г. Кузнецов, Э.Г. Куренный, А.П. Лютый Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения – Донецк:
Норд – пресс
, 2005. – 250 с. - А.К. Шидловский, Б.П. Борисов, Г.Я. Вагин, Э.Г. Куренный, И.Г. Крахмалин Электромагнитгая совместимость электроприёмников промышленных предприятий – Киев:
Наукова думка
, 1992. – 236 с. - ГОСТ 13109 – 97 Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения [Электронный ресурс]. – Режим доступа: http://rgost.ru/....
- А.К. Шидловский, Э.Г. Куренный Введение в статистическую динамику систем электроснабжения – Киев:
Наукова думка
, 1984. – 273 с. - А.К. Шидловский, В.Г. Кузнецов Повышение качества энергии в электрических сетях – Киев:
Наукова думка
, 1985. – 268 с. - Салтыков А.В. Электромагнитная совместимость параллельных дуговых сталеплавильных печей с системой электроснабжения – Диссертация кандидата технических наук, Самара, 2006 [Электронный ресурс]. – Режим доступа: http://www.dissercat.com/....
- А.А. Ермилов Основы электроснабжения промышленных предприятий – М.: Энергоатомиздат, 1983. – 208 с.
- И.В. Жежеленко, Ю.Л. Саенко Показатели качества электроэнергии и их контроль на промышленных предприятиях – М.: Энергоатомиздат, 2000. – 252 с.
- Э.Г. Куренный, Е.Н. Дмитриева, А.П. Лютый, О.А. Сидоренко Оценка и нормирование несимметрии напряжений в системах электроснабжения общего назначения – Электричество, 2008, №4. – с. 18-26.
- В.Г. Кузнецов, Е.Г. Курінний, О.П. Лютий Електромагнітна сумісність. Доза несиметрії напруги – Технічна електродинаміка, 2005, №3. – с. 49-53.
