DonNTU   Masters' portal

Aperçu

Sommaire

Introduction

Système "La bille sur le rail" (en anglais – "ball on beam") – c'est un exemple classique d'un système dynamique en thèorie du contrôle. Il est composè du rail longue, qui se fixent avec un moteur dans le centre du rail et d’une bille, qui se dèplace du plan supérieur du rail. Le mouvement du rail provoque la roulement de bille avec une accélération, qui est proportionnelle à l'angle du rail et la masse de bille.

Le système de "La bille sur le rail" est instable, quand les liaisons de stabilisation sont absents. Par conséquent, pour stabiliser le système nécessite l'utilisation d'algorithmes de contrôle basée sur l'information de la coordonnée actuelle de l'objet mobile.

Quand une personne tente de stabiliser la bille dans les mains redressé, il utilise une information visuelle et tactile. Notre objectif consiste à élaborer analogique électromécanique d'un tel système biologique.

1. Actualité de la thèse

Actualité de la thèse est la nécessité d'améliorer les algorithmes de ñontrôle du mouvement d'une bille sur un plan incliné et motorisé par retour sensoriel tactile à partir d’une peau artificielle.

2. Buts et problèmes de la recherche

Les points principaux de la recherche sont:

  1. Revue bibliographique des systèmes de la commande par d'une bille sur des rails motorisés;
  2. Élaboration d’un modèle matematique de la surface motorisée pour l'équilibrance de la bille;
  3. Élaboration d'un prototype de de la surface motoriseée par de moteur à courant continu à aimant permanent;
  4. Élaboration d’un modèle matematique du côntroleur, qui utilise les conceptions de la commande et retours sensoriels differentes;
  5. Revue de la littérature et concepts actuels de la réalisation d'une peau artificielle;
  6. L’élaboration de la commande en regulateur PID linéaire et RNA en utilisant les types differents des retours sensoriels de la position de la bille;
  7. Recherches expérimentales sur fonctionnement du système par l'influence des retours sensoriels et les algorithmes proposés;
  8. Estimation de la fiabilité du système proposé.

3. Revue bibliographique des systèmes de la commande par d'une bille sur des rails motorisés

Il existe une très grande variété d’approches lesquelles peuvent être utilisées pour la commande de système bien connus en automatique comme la bille sur le rail: le régulateur proportionnel dérivé (PD) [1], le régulateur proportionnel intégral dérivé (PID) [2], le régulateur linéaire quadratique (angl. Linear quadratic regulator, LQR) [3] et le régulateur linéaire quadratique gaussienne (angl. Linear quadratic Gaussian control, LQG) [4], le contrôle robuste [5], contrôle à structure variable (CSV) [6], la logique floue [7, 8] et réseaux de neurones [9], La linéarisation de rétroaction en négligent certains termes singuliers peut être utilisée [10], parce que le degré relatif de système n'est pas bien définie au certain point singulier de l'espace des phases. Cependant, cette approche ne fonctionne pas bien lorsque le système est loin des singularités, en raison d'une erreur d'approximation qui est généré par les termes négligés. La loi de commande avec commutation a été proposé dans [11]: îun contrôleur qui utilise la linéarisation exacte de rétroaction lorsque le système est dans la région éloignée des singularités et un autre contrôleur de linéarisation approximative de rétroaction lorsque le système se rapproche des singularités. Un contrôleur de suivi non-linéaire est connue [12], qui est basé sur la méthode du pas de pèlerin (backstepping) approximative, et les résultats des simulations montrent que ce contrôleur réalise meilleur l'erreur d'état stable par rapport aux autres méthodes d'approximation. D’autres approches ont donc été envisagées pour contrôler le système considéré à la base d'un contrôleur à logique floue [7, 8], d'interpolation [15], des réseaux neuronaux [9], et d'un contrôleur génétique [17]. Les techniques des réseaux de neurones [11] permettent de réaliser le contrôleur de l'équilibre du système assez efficacement en utilisant une population de contrôleurs de réseaux de neurones qui évoluent vers un contrôleur optimal grâce à l'utilisation d'un algorithme génétique. Une approche hybride réalise un contrôle linéaire près de la condition nominale [15] et il est utilisé avec souvent pour le problème de contrôle considère. Le contrôle de la saturation globale garantie de stabilité asymptotique est présenté dans [16].

Une autre étude importante du système de la bille sur le rail est l'utilisation de systèmes de vision dans les applications de commande de mouvement. Le contraintes de temps-réel, c'est le problème le plus important qui limite les applications de la vision [17] et qui limite la robustesse au bruit dans l'image ainsi que les perturbations causées par la scène de fond et des objets de premier plan et aux conditions d'éclairage non-idéales. Pour minimiser l'influence des ces facteurs on utilise un filtre de Kalman pour prédire la position la bille sur le rail [18].

4. Élaboration d’un modèle matematique de la surface motorisée pour l'équilibrance de la bille

Système "La bille sur le rail" est composè du rail longue, qui se fixent avec un moteur dans le centre du rail et d’une bille, qui se dèplace du plan supérieur du rail. La figure 1 décrit le comportement de la "La bille sur le rail".

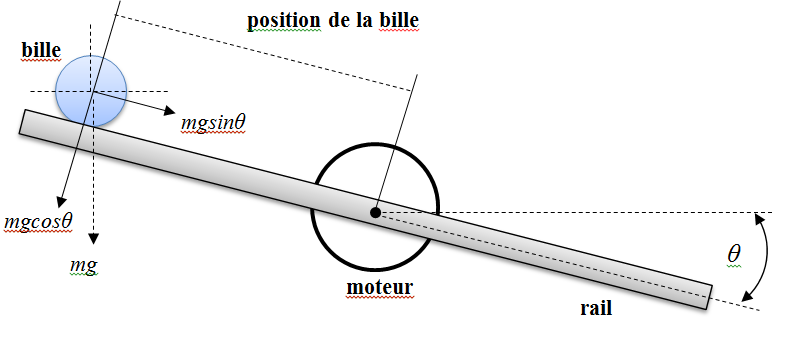
Figure 1 - Dynamique du système

Figure 1 – Dynamique du système "La bille sur le rail"

Dynamique du système peut être décrit par les équations suivantes [2]:

à) la loi de roulement de bille

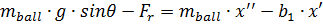
où Fr – la force de contrainte de roulement sur la bille; b1 – constante de friction (on peut négliger); mball – masse de la bille; g – accélération de la gravité θ – angulaire de déplacement de la rail; x – déplacement de la bille.

b) les équations du système électromécanique

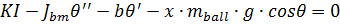
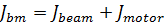
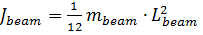
où Jmotor – moment d'inertie du moteur; Jbeam – moment d'inertie du rail; mbeam – masse de la bille; Lbeam – longueur du rail.

Sur la base d'un mod?le dynamique dans cette section produit de simulation du syst?me "La bille sur le rail".

Dans un environnement de simulation de réalité virtuelle WebotsTM on a créé la modèle

Les principales fonctionnalités de l'environnement de simulation "Webots" sont: la simulation de la cinématique et la dynamique d'un système, l'intégration des différents systèmes de capteurs tels que la vision ou capteurs tactiles, des scénarios pour des tâches de contrôle complexes, la visualisation et l'intégration des systèmes réels dans la boucle de simulation [19].

Figure 2 - Modèle Webots

Figure 2 – Modèle Webots: 1 – capteurs laser de distance; 2 – bille métallique (32 grammes); 3 – support actif articulé 4 – rail (20 sm)

Pour la commande de système "la bille sur le rail" nous avons utilisé la méthode classique – le régulateur proportionnel dérivé (PD-régulateur).

La loi de commande est décrit par les équations suivantes:

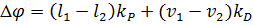
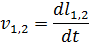
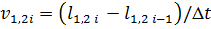
où Δφ – le signal de correction; l1, l2 – distance entre le bille et le capteur 1 ou 2 respectivement; v1, v2 – vitesses de déplacement de la bille; kP – coefficient proportionnel; kD – coefficient différentiel; Δt – pas de calcul.

Les résultats sont présentés sur la figure 3. Au points d'intersection de courbes (bleu et rouge) s’effectué la stabilisation (cf. fig. 3a).

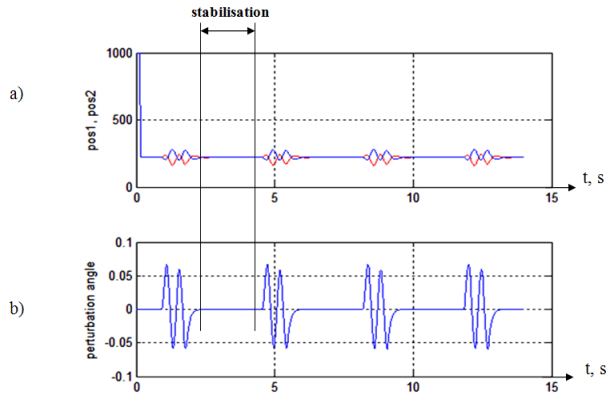
Figure 3 - Les résultats de la simulation: a) stabilisation, b) petrurbations externes

Figure 3 – Les résultats de la simulation: a) stabilisation; b) petrurbations externes

Choix des coefficients kP et kD est réalisé par la méthode itérative. Tout d'abord, on a déterminé la valeur du coefficient de proportionnalité (la valeur du coefficient différentiel on a mis zéro). Critère de choix du coefficient proportionnel optimal – la durée maximale (Tmax) de trouver la bille sur le plan 1D.

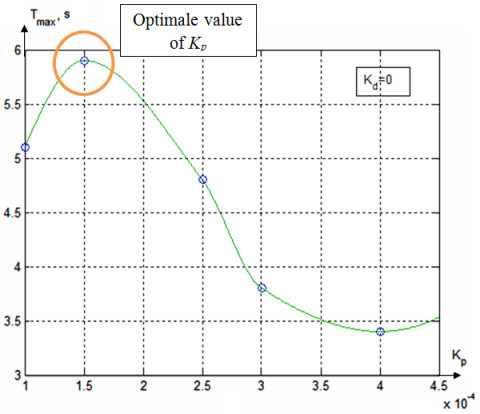
Figure 4 –Durée maximale de trouver la bille sur le plan 1D de kP

Figure 4 – Durée maximale de trouver la bille sur le plan 1D de kP

Ce graphique montre que le temps maximal de trouver la bille sur le plan 1D correspond à kP = 0,00015. Les résultats obtenus par simulation sont présentés sur la figure 5.

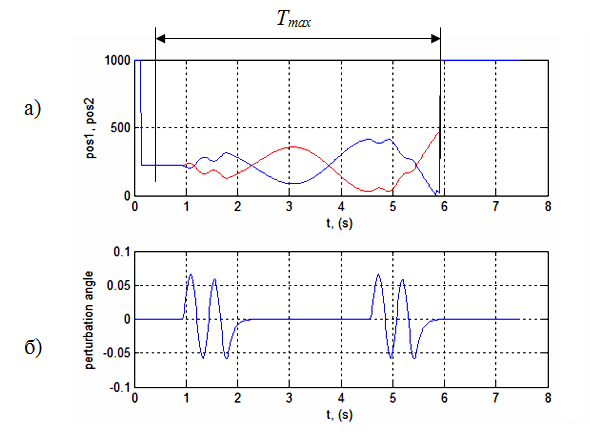
Figure 5 – Résultats de simulation (kP =0,00015 ; kD =0): a) durée maximale de trouver la bille sur le plan 1D; b) petrurbations externes

Figure 5 – Résultats de simulation (kP = 0,00015; kD = 0): a) durée maximale de trouver la bille sur le plan 1D; b) petrurbations externes

Ensuite, on a trouvé la valeur de kD, correspondant à kP = 0,00015. Critère de sélection – le temps maximale (Tstab) à laquelle la bille sera dans la stabilisation. Les résultats sont présentés sur la figure 6.

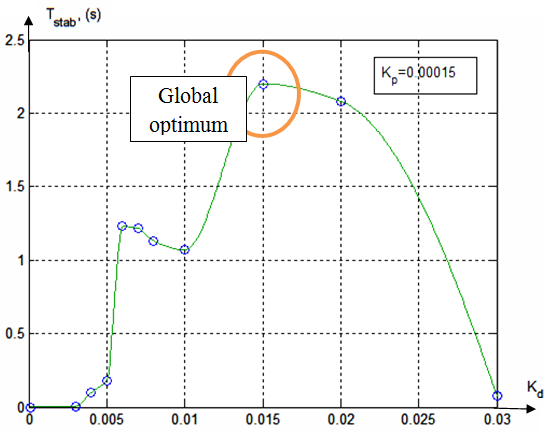
Figure 6 – Temps maximale (Tstab) à laquelle la bille sera dans la stabilisation de kD

Figure 6 – Temps maximale (Tstab) à laquelle la bille sera dans la stabilisation de kD

Sur la fig.7 on peut voir un optimum local Tstab = 1,23 au kD = 0,006 et un optimal global Tstab = 2,2 au kD = 0,015. Dans l’optimum local, le système de stabilisation se conduit plus mauvais que l'optimum global (cf. fig. 7 et 8 par comparaison)

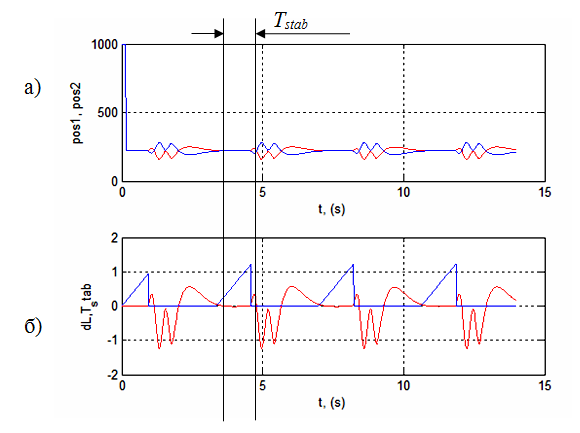
Figure 7 – Résultats de simulation à optimum local (kD =0,006; kP =0,00015 ): a) stabilisation; b) décalage du bille par rapport au centre du plan (dL) et le temps maximale (Tstab) à laquelle la bille sera dans la stabilisation

Figure 7 – Résultats de simulation à optimum local (kD = 0,006; kÐ = 0,00015 ): a) stabilisation; b) décalage du bille par rapport au centre du plan (dL) et le temps maximale (Tstab) à laquelle la bille sera dans la stabilisation

Figure 8 – Résultats de simulation à optimum global (kD =0,015; kP =0,00015 ): a) stabilisation; b) décalage du bille par rapport au centre du plan (dL) et le temps maximale (Tstab) à laquelle la bille sera dans la stabilisation

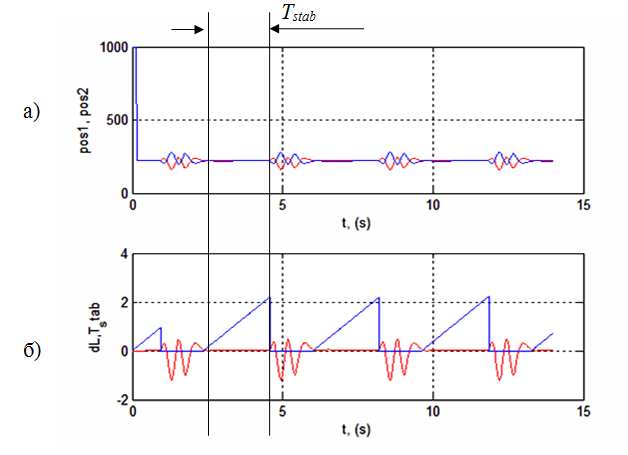
Figure 8 – Résultats de simulation à optimum global (kD = 0,015; kÐ = 0,00015 ): a) stabilisation; b) décalage du bille par rapport au centre du plan (dL) et le temps maximale (Tstab) à laquelle la bille sera dans la stabilisation

Deuxième itération de l’algorithme de choix des coefficients du régulateur PD: on a laissé kD = 0,015 et on a encore varié kP.

Figure 19 - Résultats de débogage de coefficient kP (kD=0,015)

Figure 9 - Résultats de débogage de coefficient kP (kD = 0,015)

Sur la figure 9 optimum local– Tstab = 2,15 au kP = 0,0004 et le optimal global – Tstab = 2,27 au kP = 0,0001.

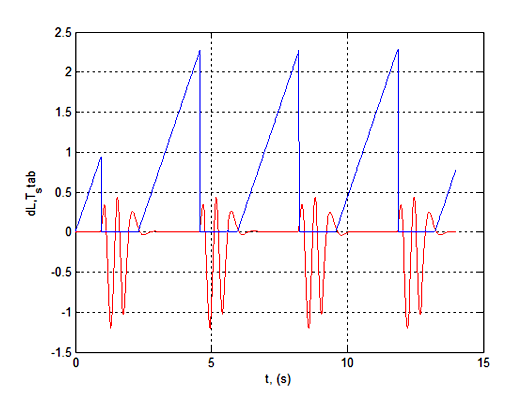
Figure 10 - Décalage du bille par rapport au centre du plan (dL) et le temps maximale (Tstab) à laquelle la bille sera dans la stabilisation pour les valeurs optimales de kP et kD (kP=0,0001; kD=0,015)

Figure 10 – Décalage du bille par rapport au centre du plan (dL) et le temps maximale (Tstab) à laquelle la bille sera dans la stabilisation pour les valeurs optimales de kP et kD (kP = 0,0001; kD = 0,015)

Pour vérifier l'exactitude du système, nous avons modélisé ce système dans Simulink. Le déplasement d'une bille roulant sur un plan incliné est décrit par les expressions (1)-(4).

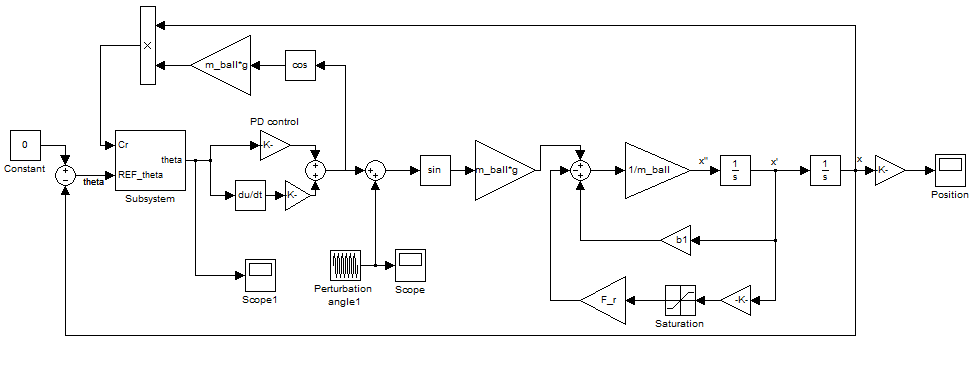
Figure 11 ? Modèle Simulink du système

Figure 11 – Modèle Simulink du système "La bille sur le rail"

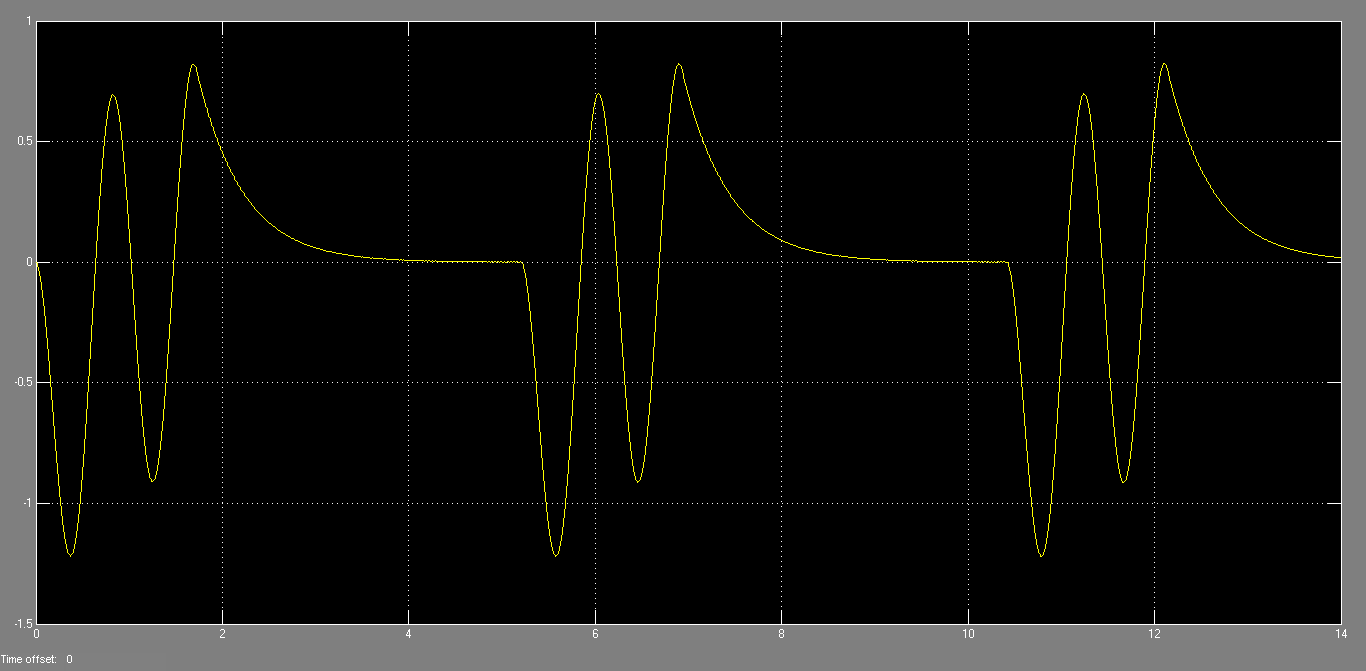
Figure 12 ? Décalage du bille par rapport au centre du rail et petrurbations externes

Figure 12 – Décalage du bille par rapport au centre du rail et petrurbations externes

Les résultats obtenus dans Simulink sont quelque peu différentes à partir des résultats obtenus dans Webots. Ceci peut être expliqué par le fait que, dans Webots pour la description des propriétés physiques de la bille, on peut définir des propriétés telles que densité, la rebondir, vitesse de rebond, frottement de Coulomb, glissement vigueur dépend, tandis que dans Simulink, nous considérons seulement la masse et la friction de la bille.

5. Élaboration d’une installation expérimentale avec un plan 1D motorisé

Animation: 7 cadres, 5 repetition, duration de chaque cadre - 120 ms, 298 Êá

Figure 13 – Installation expérimentale 1D: 1 – capteurs de distance; 2 – moteur Maxon (motor + réducteur + encoder); 3 – motor controller Maxon EPOS 24/1

Conclusion

Dans ce rapport est présenté un bref aperçu du système de la bille sur le rail avec la modélisation et plusieurs de réalisations. Les environnement de simulation de réalité virtuelle WebotsTM utilisés pour la conception du système de bille sur le rail nous a permis de tester l'algorithme de contrôle proposé. Les coefficients optimaux d'un contrôleur simple PD pour le système bille sur rail peut être établie dans les 2 itérations. Simulation d'un même système dans Simulink nous a permis de vérifier les résultats et de vérifier leur authenticité.

Bibliographie

  1. Yu W. Nonlinear PD regulation for ball and beam system // International Journal of Electrical Engineering Education. – Vol. 46, No.1. – 2009. – P. 59-73.
  2. Hamed B. Application of a LabVIEW for Real-Time Control of Ball and Beam System // IACSIT International Journal of Engineering and Technology. – Vol. 2, No.4. – 2010. – P. 401-407.
  3. Marton L., Hodel A.S., Lantos B., Hung J.Y. Underactuated Robot Control: Comparing LQR, Subspace Stabilization, and Combined Error Metric Approaches // IEEE Transactions on Industrial Electronics. – Vol. 55, no.10. – 2008. – Ð. 3724-3730.
  4. Bryson A.E., Ho Y.G. Applied Optimal Control // N.Y: Hemisphere, 1975.
  5. Huang J., Lin C.F. Robust nonlinear control of the ball and beam system // Proceedings of the American Control Conference, 1995. – Vol. 1. – P. 306-310.
  6. Almutairi N.B., Zribi M. On the sliding mode control of a Ball on a Beam system // Springer Tracts in Nonlinear Dynamics, 2009. – Vol. 59, Num. 1-2. – 2009. – P. 221-238.
  7. Guo Y., Hill D.J., Jiang Z.P. Global nonlinear control of the ball and beam system // Proceedings of the 35th IEEE Conference on Decision and Control. – Vol. 3. – 11-13 Dec,1996. – P. 2818-2823.
  8. YI J., Yubazaki N., Hirota K. Stabilization Control of Ball and Beam Systems // International Conference IFSA World Congress and 20th NAFIPS, 2001, Joint 9th Vol. 4. – P. 2229-2234.
  9. Eaton P.H., Prokhorov D.V., Wunsch D.C. Neurocontroller Alternatives for Fuzzy Ball and Beam Systems with Nonuniform Nonlinear Friction // IEEE Transactions of the Neural Networks, March 2000. – Vol. 11, No 2. – P. 423-435.
  10. Hauser J., Sastry S., Kokotovic P. Nonlinear control via approximate input-output linearization: the ball and beam example // IEEE Transactions on Automatic Control.– Vol. 37. – Issue: 3. – March 1992. – P. 392-398.
  11. Tomlin C.J., Sastry S. Switching through singularities // Proceedings of the 36th IEEE Conference on Decision and Control. – Vol. 1. – 1997. – P. 1-6.
  12. Lai M.C., Chien C.C., Cheng C.Y., Xu Z., Mang Y. Nonlinear Tracking Control Via Approximate Backstepping // Proceedings of the American Control Conference, 1994. – Vol. 2. – 29 Jun-1 Jul. – 1994. – P. 1339-1343.
  13. Dale S., Dragomir T.L. Interpolative-type control solution for a Ball and Beam system // CEAI, Vol. 8, No. 3. – 2006. – P. 3-14.
  14. Marra M.A., Boling B.E., Walcott B.L. Genetic control of a ball-beam system // Proceedings of the 1996 IEEE International Conference on Control Applications. – 1996. – P. 608-613.
  15. Simmons A.T., Hung J.Y. Hybrid Control of Systems with Poorly Defined Relative Degree: The Ball on Beam Example // 30th Annual Conference of IEEE Industrial Electronics Society, 2004. – Vol 3. – P. 2436-2440.
  16. Barbu C., Sepulchre R., Lin W., Kokotovic P.V. Global Asymptotic Stabilization of the Ball-and-Beam System // Proceedings of the 36th IEEE Conference on Decision and Control. – 1997. – P. 2351-2355.
  17. Petrovic I., Brezak M., Cupec R. Machine vision based control of the ball and beam // 7th International Workshop Advanced Motion Control. – 2002. – P. 573-577.
  18. Naz S.A., Katebi R., Balbis L. Implementation of Kalman Filter on Ball And Beam Experiment Using Labview // International Conference Control 2006, Glasgow.
  19. Michel O. Webots: Professional Mobile Robot Simulation // International Journal of Advanced Robotic Systems. – Vol. 1, Num. 1, – P. 39-42.
  20. http://www.labview.ru/labview/what_is_labview/index.php