ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

Система «балансир и шар» (англ. "ball on beam") – это классический пример динамической системы в теории управления. Она состоит из длинной балки (балансир), в центре которой фиксируется двигатель, и шарика, который движется по верхней плоскости балки. Наклон балки провоцирует качение шарика с ускорением, которое пропорционально углу наклона балансира и массе шарика.

Система «балансир и шар» при отсутствии стабилизирующей связи о положении шарика является неустойчивой, она существенно нелинейна при больших углах отклонения шарика. Поэтому для стабилизации системы необходимо применение алгоритмов управления основанных на информации о текущей координате движущегося объекта.

В двухмерном измерении система «балансир и шар» представлена как система «шар и платформа» (англ. "ball on plate"), где шар катится по поверхности платформы, положение которой можно регулировать, наклоняя ее вперед, назад, влево или вправо.

Когда человек пытается стабилизировать шарик на своей расправленной ладони, то в качестве обратной связи он использует визуальную и тактильную информацию. Перед нами стоит задача разработки электромеханического аналога подобной биологической системы.

1. Актуальность темы

Актуальность темы заключается в необходимости повышения качества управления движением сфероподобных объектов на моторизированной двумерной плоскости при помощи искусственной кожи. Новизна работы состоит в применении биологически-подобных принципов управления нелинейными электромеханическими объектами и совершенствовании математических моделей с учетом системы управления. Оценена надежность предложенной системы. Работа выполняется в рамках международного французско-украинского исследовательского проекта «Днепр».

2. Цель работы и задачи исследования

Целью работы является усовершенствование алгоритмов управления движением сфероподобных объектов на моторизированной плоскости при помощи тактильной обратной связи с использованием искусственной кожи и оценка надежности предложенной системы.

Основные вопросы, которые решаются в магистерской работе:

  1. Библиографический обзор существующих систем управления движением сфероподобных объектов на плоскости;
  2. Разработка математической модели моторизированной плоскости для уравновешивания катящегося сферического объекта;
  3. Разработка прототипа моторизированной плоскости на базе микромашины постоянного тока с постоянными магнитами;
  4. Разработка математической модели контроллера с использованием различных структур системы управления и датчиков обратной связи;
  5. Обзор существующих подходов к реализации искусственной кожи;
  6. Разработка алгоритма управления на базе классического ПИД регулятора и нейронной сети с реализацией обратных связей по положению сферического объекта в плоскости;
  7. Экспериментальные исследования предложенного алгоритма управления и влияние на его работу типа обратной связи;
  8. Оценка надежности разработанной системы.

3. Существующие системы управления движением сфероподобных объектов на плоскости 1D

Существует огромное количество методов, подходов, которые используются для управления движением сфероподобных объектов на плоскости 1D. В теории управления хорошо известны следующие принципы управления системой «балансир и шар»: пропорционально-дифференциальное регулирование (ПД) [1], пропорционально-интегрально-дифференциальное регулирование (ПИД) [2], линейно-квадратичное (англ. Linear quadratic regulator, LQR) [3] и линейно-квадратичное гауссовское управление (англ. Linear quadratic Gaussian control, LQG) [4], робастное управление [5], управление с переменной структурой (CSV) [6], нечеткая логика [7, 8] и нейронные сети [9], так же может быть использована линеаризация обратной связи [10]. Однако этот подход не работает, когда система находится далеко от сингулярности, в связи появлением относительной ошибки. Закон управления с переключением регуляторов был предложен в [11]: один контроллер, который использует точную линеаризацию обратной связи, когда система находится в зоне, удаленной от сингулярности и другой регулятор с относительной линеаризацией обратной связи, если система приближается к сингулярности. Нелинейный следящий регулятор представлен в работе [12], он основан на методе backstepping, результаты моделирования показывают, что этот подход обеспечивает лучшую устойчивость по сравнению с другими приближенными методами. Существуют и другие подходы к управлению системой, основанные на управлении с применением нечеткой логики [7, 8], интерполяции [15], нейронных сетей [9], а также генетический принцип параметризации контроллера [17]. Методы нейронных сетей [11] позволяют реализовать устойчивое управление системой. Гибридный подход реализуется совместно с линейным управлением при почти номинальных условиях [15] и часто используется для проверки рассматриваемой задачи. В работе [16] управление глобальным насыщением гарантирует асимптотическую устойчивость.

Часто в системе «балансир и шар» используется техническое зрение. Ограничения в режиме реального времени – это самая важная проблема, которая ограничивает применение технического зрения [17] и устойчивость, так же существуют сложности определения объекта переднего плана при плохих условиях освещения. Для минимизации влияния этих факторов используют фильтры Калмана для определения положения шара [18].

4. Разработка математической модели моторизированной плоскости со катящимся сферическим объектом

Система «балансир и шар» состоит из двух частей: балансир, который вращается вместе с валом двигателя, а также шарик, который катится с некоторым ускорением в соответствии с изменением угла наклона балки. На рисунке 1 описано поведение системы «балансир и шар».

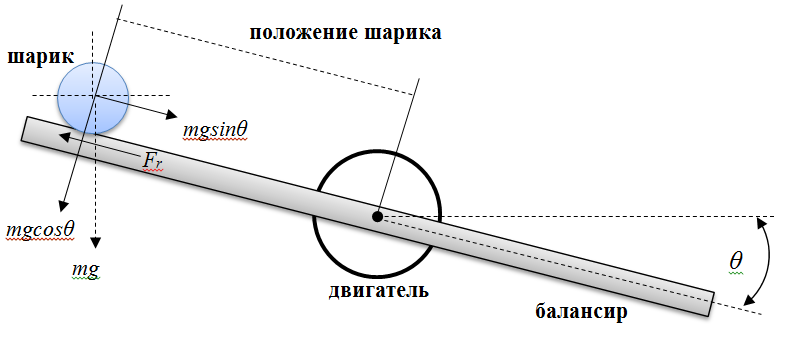
Динамика системы «шар и балансир»

Рисунок 1 – Динамика системы «шар и балансир»

Динамику системы можно описать следующими уравнениями [2]:

а) уравнения движения шара по поверхности балансира

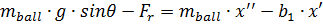
где Fr – сила сопротивления качению шара; b1 – коэффициент трения (пренебрежительно мал); mball – масса шарика; g – ускорение силы тяжести; θ – угол наклона балки; x – перемещение шарика.

б) уравнения электромеханической системы

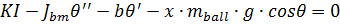
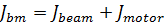
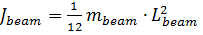
где Jmotor – момент инерции двигателя; Jbeam – момент инерции балансира; mbeam – масса шарика; Lbeam – длинна балансира.

На основе динамической модели, в данном разделе произведено моделирование системы «балансир и шар».

Моделирование выполнено с помощью программного обеспечения WebotsTM, при этом принято, что система в зоне функционирования нелинейна.

Основные возможности моделирования окружающей среды "Webots": моделирование кинематики и динамики системы, интеграции различных систем датчиков, искусственное зрение и тактильные сенсоры, сценарии для сложных задач управления, визуализации и интеграции реальных систем [19].

Модель Webots

Рисунок 2 – Модель Webots:1 – лазерные датчики расстояния; 2 – металлический шарик (32 г); 3 – электропривод; 4 – балансир (20 см)

Для управления системой «балансир и шар» используем классический метод – пропорционально-дифференциальное регулирование (ПД-контроль).

Закон управления описывается следующими уравнениями:

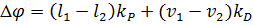
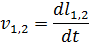
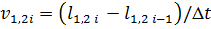
где Δφ – корректирующий сигнал; l1, l2 – расстояния между шариком и датчиками 1 или 2 соответственно; v1, v2 – скорости перемещения шарика; kP – коэффициент пропорциональности; kD – дифференциальный коэффициент; Δt – шаг расчета.

Результаты представлены на рис.3. В точке пересечений линий (синяя и красная) происходит стабилизация шара (см. рис. 3a).

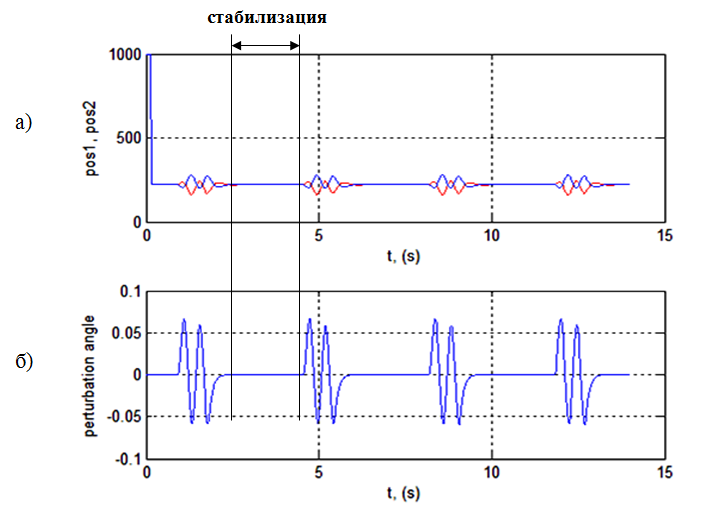
Результаты симулирования Webots

Рисунок 3 – Результаты симулирования: a) стабилизация; б) внешние возмущения

Выбор коэффициентов kP и kD осуществляется методом подбора. Для начала, определяем значение коэффициента пропорциональности, при этом значение дифференциального коэффициента принимаем равным нулю. В качестве критерия подбора выбираем максимальное время (Tmax) нахождения шарика на платформе 1D при стабилизации.

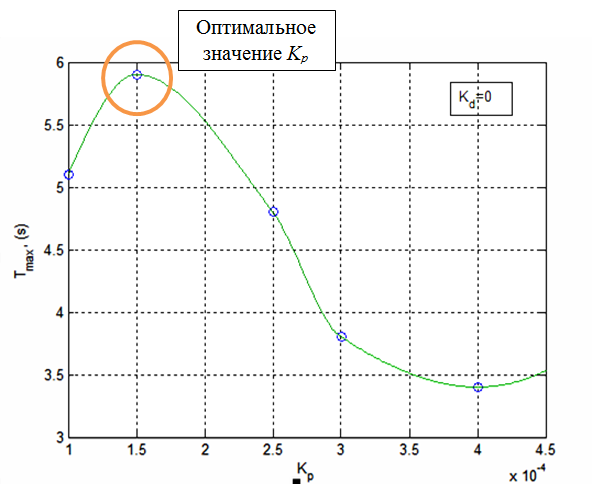
Максимальная продолжительность нахождения шарика на платформе 1D в зависимости от kP

Рисунок 4 – Максимальная продолжительность нахождения шарика на платформе 1D в зависимости от kP

По полученным результатам, можно сделать вывод, что максимальной продолжительности нахождения шарика на балансире соответствует kP = 0,00015. Полученные результаты симулирования представлены на рисунке 5.

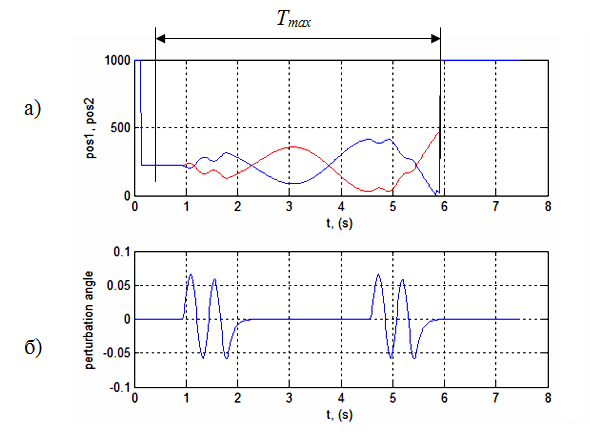
Результаты моделирования (kP =0,00015 ; kD =0): a) максимальная продолжительность нахождения шарика на платформе 1D, б) внешние возмущения

Рисунок 5 – Результаты моделирования (kP = 0,00015; kD = 0): a) максимальная продолжительность нахождения шарика на платформе 1D; б) внешние возмущения

Далее, находим значение коэффициента kD, соответствующего оптимальному значению kP = 0,00015. Критерий выбора – максимальное время (Tstab) стабилизации шарика. Результаты представлены на рисунке 6.

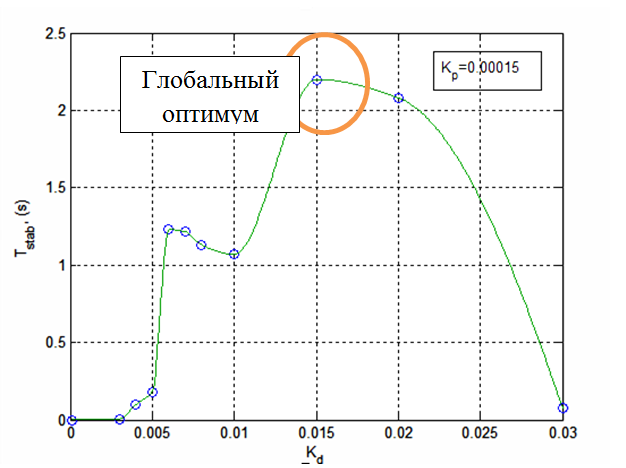
Максимальное время (Tstab) стабилизации шарика в зависимости от kD

Рисунок 6 – Максимальное время (Tstab) стабилизации шарика в зависимости от kD

На рис.6 можно видеть локальный оптимум соответствующий Tstab = 1,23 при kD = 0,006 и глобальный оптимум, соответствующий Tstab = 2,2 при kD = 0,015. При локальном оптимуме система стабилизации ведет себя хуже, чем при глобальном оптимуме (см. рис. 7 и 8 для сравнения).

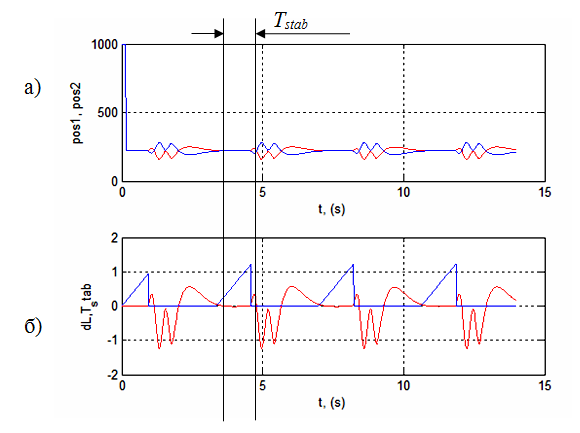
Рисунок 7 – Результаты симулирования при локальном оптимуме (kD =0,006; kP =0,00015 ): a) стабилизация; б) положение шарика (dL) относительно центра балансира; максимальное время (Tstab) стабилизации шарика

Рисунок 7 – Результаты симулирования при локальном оптимуме (kD = 0,006; kР = 0,00015 ): a) стабилизация; б) положение шарика (dL) относительно центра балансира; максимальное время (Tstab) стабилизации шарика

Рисунок 8 – Результаты симулирования глобальном оптимуме (kD =0,015; kP =0,00015 ): a) стабилизация; б) положение шарика (dL) относительно центра балансира; максимальное время (Tstab) стабилизации шарика

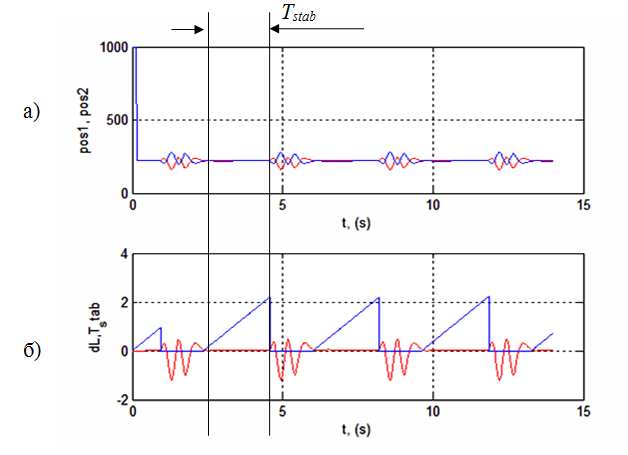
Рисунок 8 – Результаты симулирования при глобальном оптимуме (kD = 0,015; kР = 0,00015 ): a) стабилизация; б) положение шарика (dL) относительно центра балансира; максимальное время (Tstab) стабилизации шарика

Вторая итерация алгоритма выбора коэффициента PD регулятора: принимаем kD = 0,015 и изменяем значение коэффициента kP.

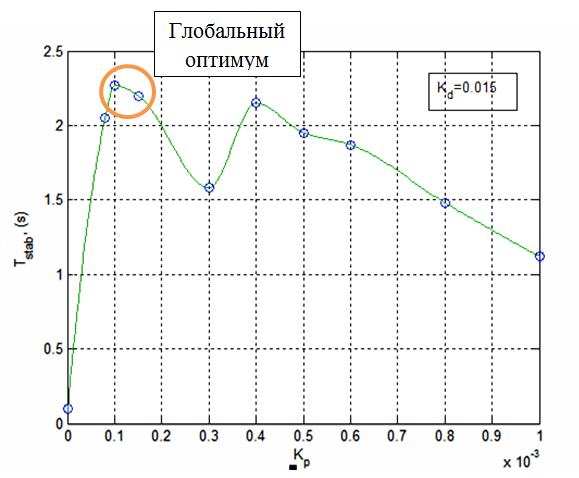
Рисунок 9 – Результаты отладки коэффициента kP (kD=0,015)

Рисунок 9 – Результаты отладки коэффициента kP (kD = 0,015)

При отладке коэффициентов так же можно наблюдать два оптимума: локальный оптимум – Tstab = 2,15 при kP = 0,0004 и глобальный оптимум – Tstab = 2,27 при kP = 0,0001.

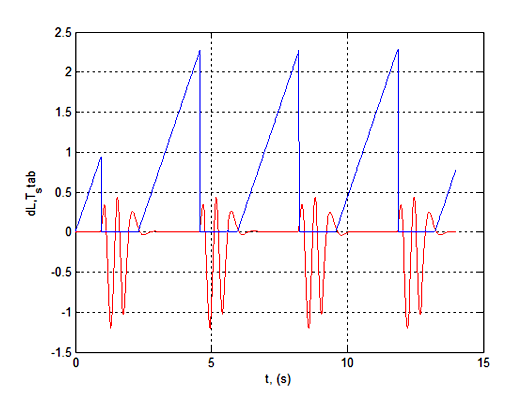
Рисунок 10 – Смещение шарика (dL) относительно центра балансира и максимальное время (Tstab) нахождения шарика в стабилизации для оптимальных значений коэффициентов kP и kD (kP=0,0001; kD=0,015)

Рисунок 10 – Смещение шарика (dL) относительно центра балансира и максимальное время (Tstab) нахождения шарика в стабилизации для оптимальных значений коэффициентов kP и kD (kP = 0,0001; kD = 0,015)

Для проверки правильности системы «балансир и шар», смоделированной в Webots, моделируем систему эту же систему в Simulink на основе уравнений (1)-(4).

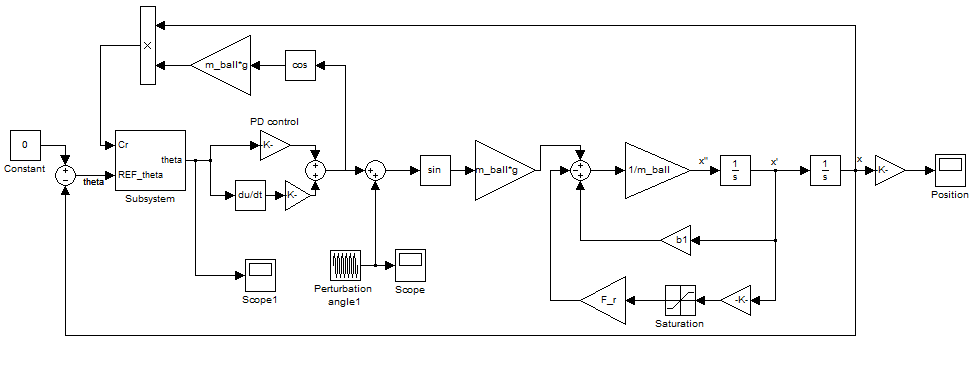
Рисунок 11 – Модель Simulink системы «балансир и шар»

Рисунок 11 – Модель Simulink системы «балансир и шар»

Результаты моделирования приведены на рис. 12.

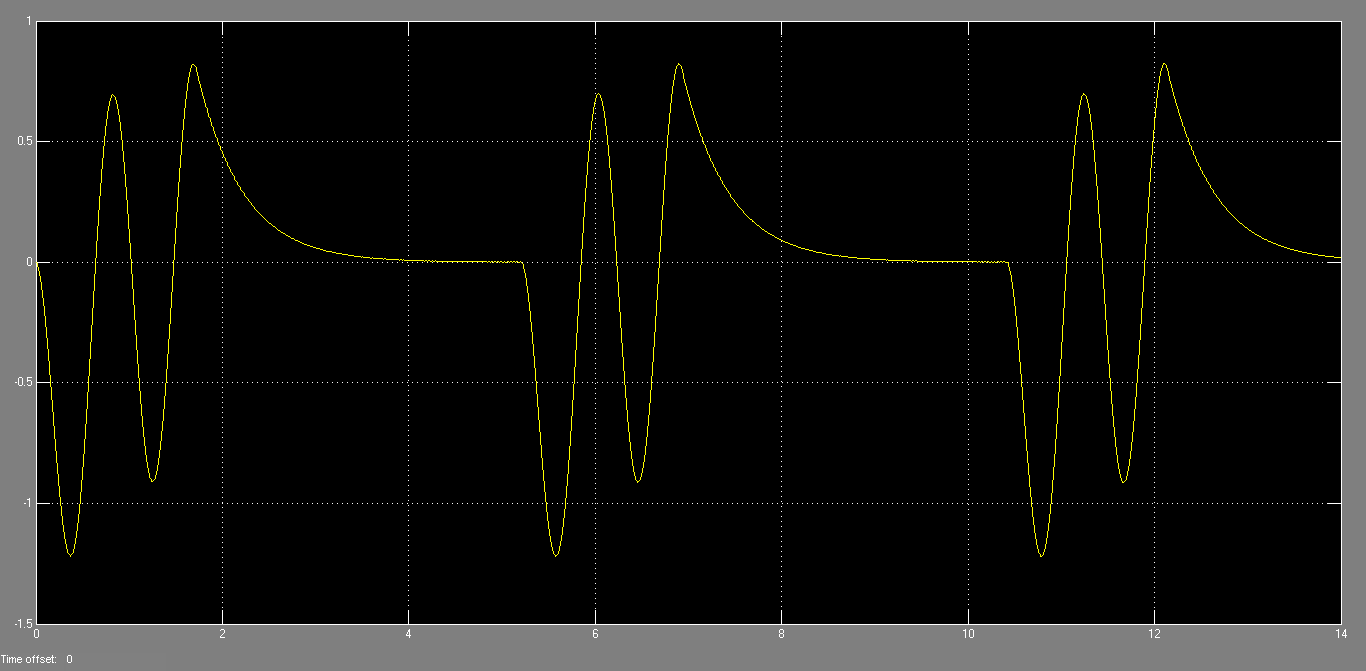
Рисунок 12 - Смещение шарика относительно центра балансира

Рисунок 12 – Смещение шарика относительно центра балансира

Результаты, полученные в Simulink несколько отличаются от результатов, полученных в Webots. Это может объяснено тем, что в Webots для описания физических свойств шарика мы можем задавать такие свойства как плостность, упругость, кулоновское трение, сила зависимого скольжения, в то время как в Simulink мы учитываем только массу и трение шарика.

5. Создание экспериментального образца моторизированного балансира 1D

Анимация: 7 кадр, 5 повторений, длительность каждого кадра - 120 мс, 298 Кб

Рисунок 13 – Экспериментальная установка моторизированного балансира 1D: 1 – датчики расстояния; 2 – микродвигатель Maxon (двигатель, редуктор, датчик углового положения); 3 – контроллер двигателя Maxon EPOS 24/1

Используем преимущества современной среды графического программирования LabView [20], для графического программирования задачи автоматизации научного эксперимента: разработки и тестирования алгоритмов управления, обработки и анализа сигналов датчиков , управления двигателем посредством контролера Maxon EPOS 24/1, создания интерфейса пользователя и отображение данных.

Выводы

Моделирование широко используется при решении различных технических и научных проблем. Применяются сложные инструменты моделирования для точного учета процессов, протекающих в электромеханических системах. Моделирование в программном обеспечении WebotsTM системы «балансир и шар» позволило нам проверить предложенный алгоритм управления, определить оптимальные коэффициенты простого ПД-регулятора. Установлено, что параметры системы управления могут быть определены после двух итераций работы модели. Моделирование этой же системы в Simulink позволило нам проверить полученные результаты и убедиться в их достоверности.

Дальнейшая работа предполагает развитие методов биологически-подобного управления и экспериментальные исследования на разработанной физической модели объекта.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2012 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Yu W. Nonlinear PD regulation for ball and beam system // International Journal of Electrical Engineering Education. – Vol. 46, No.1. – 2009. – P. 59-73.
  2. Hamed B. Application of a LabVIEW for Real-Time Control of Ball and Beam System // IACSIT International Journal of Engineering and Technology. – Vol. 2, No.4. – 2010. – P. 401-407.
  3. Marton L., Hodel A.S., Lantos B., Hung J.Y. Underactuated Robot Control: Comparing LQR, Subspace Stabilization, and Combined Error Metric Approaches // IEEE Transactions on Industrial Electronics. – Vol. 55, no.10. – 2008. – Р. 3724-3730.
  4. Bryson A.E., Ho Y.G. Applied Optimal Control // N.Y: Hemisphere, 1975.
  5. Huang J., Lin C.F. Robust nonlinear control of the ball and beam system // Proceedings of the American Control Conference, 1995. – Vol. 1. – P. 306-310.
  6. Almutairi N.B., Zribi M. On the sliding mode control of a Ball on a Beam system // Springer Tracts in Nonlinear Dynamics, 2009. – Vol. 59, Num. 1-2. – 2009. – P. 221-238.
  7. Guo Y., Hill D.J., Jiang Z.P. Global nonlinear control of the ball and beam system // Proceedings of the 35th IEEE Conference on Decision and Control. – Vol. 3. – 11-13 Dec,1996. – P. 2818-2823.
  8. YI J., Yubazaki N., Hirota K. Stabilization Control of Ball and Beam Systems // International Conference IFSA World Congress and 20th NAFIPS, 2001, Joint 9th Vol. 4. – P. 2229-2234.
  9. Eaton P.H., Prokhorov D.V., Wunsch D.C. Neurocontroller Alternatives for Fuzzy Ball and Beam Systems with Nonuniform Nonlinear Friction // IEEE Transactions of the Neural Networks, March 2000. – Vol. 11, No 2. – P. 423-435.
  10. Hauser J., Sastry S., Kokotovic P. Nonlinear control via approximate input-output linearization: the ball and beam example // IEEE Transactions on Automatic Control.– Vol. 37. – Issue: 3. – March 1992. – P. 392-398.
  11. Tomlin C.J., Sastry S. Switching through singularities // Proceedings of the 36th IEEE Conference on Decision and Control. – Vol. 1. – 1997. – P. 1-6.
  12. Lai M.C., Chien C.C., Cheng C.Y., Xu Z., Mang Y. Nonlinear Tracking Control Via Approximate Backstepping // Proceedings of the American Control Conference, 1994. – Vol. 2. – 29 Jun-1 Jul. – 1994. – P. 1339-1343.
  13. Dale S., Dragomir T.L. Interpolative-type control solution for a Ball and Beam system // CEAI, Vol. 8, No. 3. – 2006. – P. 3-14.
  14. Marra M.A., Boling B.E., Walcott B.L. Genetic control of a ball-beam system // Proceedings of the 1996 IEEE International Conference on Control Applications. – 1996. – P. 608-613.
  15. Simmons A.T., Hung J.Y. Hybrid Control of Systems with Poorly Defined Relative Degree: The Ball on Beam Example // 30th Annual Conference of IEEE Industrial Electronics Society, 2004. – Vol 3. – P. 2436-2440.
  16. Barbu C., Sepulchre R., Lin W., Kokotovic P.V. Global Asymptotic Stabilization of the Ball-and-Beam System // Proceedings of the 36th IEEE Conference on Decision and Control. – 1997. – P. 2351-2355.
  17. Petrovic I., Brezak M., Cupec R. Machine vision based control of the ball and beam // 7th International Workshop Advanced Motion Control. – 2002. – P. 573-577.
  18. Naz S.A., Katebi R., Balbis L. Implementation of Kalman Filter on Ball And Beam Experiment Using Labview // International Conference Control 2006, Glasgow.
  19. Michel O. Webots: Professional Mobile Robot Simulation // International Journal of Advanced Robotic Systems. – Vol. 1, Num. 1, – P. 39-42.
  20. http://www.labview.ru/labview/what_is_labview/index.php