ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Система „балансир та шар” (англ. "ball on beam") – це класичний приклад динамічної системи в теорії управління. Вона складається з довгої балки (балансир), у центрі якої фіксується двигун, та шару, який рухається по верхній площині балки. Нахил балки провокує кочення шару з прискоренням, яке пропорційне кутові нахилу балансира і масі шару.

Система „балансир та шар” при відсутності стабілізуючого зв'язку про положення шару є нестійкою, вона істотно нелінійна при великих кутах відхилення шару. Тому для стабілізації системи необхідно застосування алгоритмів управління заснованих на інформації про поточну координату рухомого об'єкту.

У двомірному вимірі система „балансир та шар” представлена як система „шар і платформа” (англ. "ball on plate"), в якій шар котиться по поверхні платформи, положення якої можна регулювати, нахиляючи її вперед, назад, вліво або вправо.

Коли людина намагається стабілізувати шар на своїй розправленій долоні, то в якості зворотнього зв'язку він використовує візуальну й тактильну інформацію. Перед нами стоїть завдання розробки електромеханічного аналога подібної біологічної системи.

1. Актуальність теми

Актуальність теми полягає в необхідності підвищення якості управління рухом сфероподібних об'єктів на моторизованій двовимірної площині за допомогою штучної шкіри. Новизна роботи полягає в застосуванні біологічно-подібних принципів управління нелінійними електромеханічними об'єктами та вдосконаленні математичних моделей з урахуванням системи управління. Оцінена надійність запропонованої системи. Робота виконується в рамках міжнародного французько-українського дослідницького проекту „Дніпро”.

2. Мета роботи і задачі дослідження

Метою роботи є удосконалення алгоритмів керування рухом сфероподібних об'єктів на моторизованій площині за допомогою тактильного зворотного зв'язку з використанням штучної шкіри та оцінка надійності запропонованої системи.

Основні питання, які вирішуються в магістерській роботі:

  1. Бібліографічний огляд існуючих систем управління рухом сфероподібних об'єктів на площині;
  2. Розробка математичної моделі моторизованої площини для врівноваження сферичного об'єкту, що котиться;
  3. Розробка прототипу моторизованої площини на базі мікромашини постійного струму з постійними магнітами;
  4. Розробка математичної моделі контролера з використанням різних структур системи управління і датчиків зворотного зв'язку;
  5. Огляд існуючих підходів до реалізації штучної шкіри;
  6. Розробка алгоритму управління на базі класичного ПІД регулятора і нейронної мережі з реалізацією зворотних зв'язків по положенню сферичного об'єкту в площині;
  7. Експериментальні дослідження запропонованого алгоритму управління і вплив на його роботу типу зворотного зв'язку;
  8. Оцінка надійності розробленої системи.

3. Існуючі системи управління рухом сфероподобних об'єктів на площині 1D

Існує величезна кількість методів, підходів, які використовуються для управління рухом сфероподібних об'єктів на площині 1D. В теорії управління добре відомі такі принципи управління системою „балансир та шар”: пропорційно-диференціальне регулювання (ПД) [1], пропорційно-інтегрально-диференціальне регулювання (ПІД) [2], лінійно-квадратичне (англ. Linear quadratic regulator, LQR) [3] і лінійно -квадратичне гауссовское управління (англ. Linear quadratic Gaussian control, LQG) [4], робастне управління [5], управління зі змінною структурою (CSV) [6], нечітка логіка [7, 8] і нейронні мережі [9], так само може бути використана лінеаризація зворотного зв'язку [10]. Однак цей підхід не працює, коли система знаходиться далеко від сингулярності, у зв'язку з появою відносної похибки. Закон управління з перемиканням регуляторів був запропонований в [11]: один контролер, який використовує точну лінеаризацію зворотного зв'язку, коли система знаходиться в зоні, віддаленій від сингулярності та інший регулятор з відносною лінеаризацією зворотного зв'язку, якщо система наближається до сингулярності. Нелінійний слідкуючий регулятор представлений в роботі [12], він заснован на методі backstepping, результати моделювання показують, що цей підхід забезпечує кращу стійкість у порівнянні з іншими наближеними методами. Існують і інші підходи до управління системою, засновані на управлінні з застосуванням нечіткої логіки [7, 8], інтерполяції [15], нейронних мереж [9], а також генетичний принцип параметризації контролера [17]. Методи нейронних мереж [11] дозволяють реалізувати стійке управління системою. Гібридний підхід реалізується спільно з лінійним управлінням при майже номінальних умовах [15] і часто використовується для перевірки даної задачі. В роботі [16] управління глобальним насиченням гарантує асимптотичну стійкість.

Часто в системі „балансир та шар” використовується технічний зір. Обмеження в режимі реального часу - це найважливіша проблема, яка обмежує застосування технічного зору [17] і стійкість, так само існують складності визначення об'єкта переднього плану при поганих умовах освітлення. Для мінімізації впливу цих факторів використовують фільтри Калмана для визначення положення шару [18].

4. Розробка математичної моделі моторизованої площини зі сферичним об'єктом, що котиться по її поверхні

Система „балансир та шар” складається з двох частин: балансир, який обертається разом з валом двигуна, а також шар, що котиться з деяким прискоренням відповідно до зміни кута нахилу балки. На рис. 1 описана поведінка системи „балансир та шар”.

Рисунок 1 - Динаміка системи „балансир та шар”

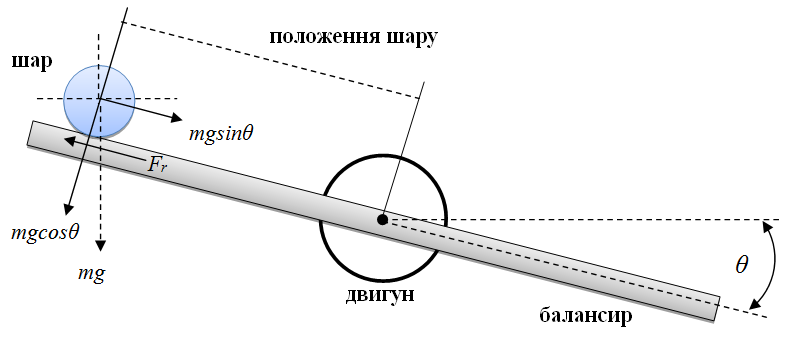
Рисунок 1 – Динаміка системи „балансир та шар”

Динаміку системи можна описати наступними рівняннями [2]:

а) рівняння руху шару по поверхні балансира

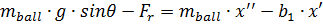
де Fr – сила опору коченню шару; b1 – коефіцієнт тертя (зневажливо малий); mball – маса шару; g – прискорення сили тяжіння; θ – кут нахилу балансира; x – переміщення шара.

б) рівняння електромеханічної системи

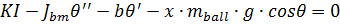
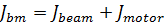
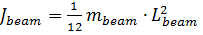
де Jmotor – момент інерції двигуна; Jbeam – момент інерції балансира; mbeam – маса шару; Lbeam – довжина балансира.

На основі динамічної моделі, в даному розділі реалізовано моделювання системи „балансир та шар”.

Моделювання виконано за допомогою програмного забезпечення WebotsTM, при цьому прийнято, що система в зоні функціонування нелінійна.

Основні можливості моделювання навколишнього середовища "Webots": моделювання кінематики і динаміки системи, інтеграції різних систем датчиків, штучний зір і тактильні сенсори, сценарії для складних завдань управління, візуалізації та інтеграції реальних систем [19].

Модель Webots

Рисунок 2 – Модель Webots:1 – лазерні датчики відстані; 2 – металевий шар (32 г); 3 – електропривод; 4 – балансир (20 см)

Для управління системою „балансир та шар” використовуємо класичний метод – пропорційно-диференціальне регулювання (ПД-контроль).

Закон управління описується наступними рівняннями:

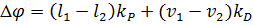
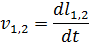
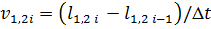
где Δφ – коригувальний сигнал; l1, l2 – відстані між шаром і датчиками 1 або 2 відповідно; v1, v2 – швидкості переміщення кульки; kP – коефіцієнт пропорційності; kD – диференціальний коефіцієнт; Δt – крок розрахунку.

Результати представлені на рис.3. У точці перетину ліній (синя і червона) відбувається стабілізація (див. рис. 3a).

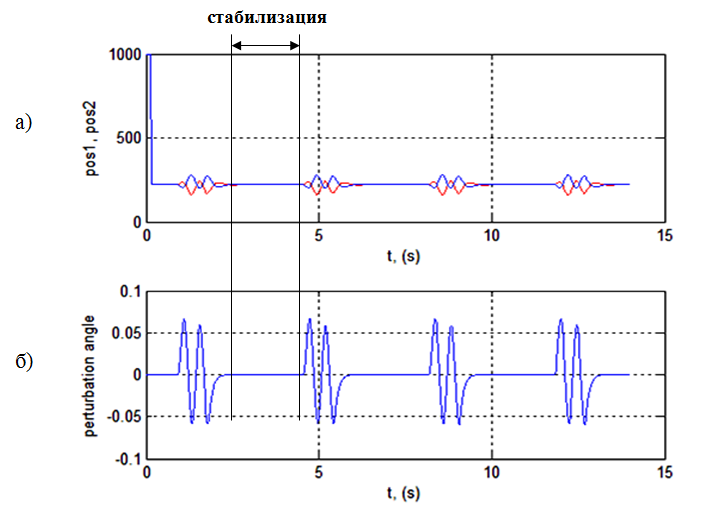
Рисунок 3 - Результати симулювання: a) стабілізація, б) зовнішні збурення

Рисунок 3 – Результати симулювання: a) стабілізація, б) зовнішні збурення

Вибір коефіцієнтів kP і kD здійснюється методом підбору. Для початку, визначаємо значення коефіцієнта пропорційності, при цьому значення диференціального коефіцієнта приймаємо рівним нулю. Як критерій підбору вибираємо максимальний час (Tmax) знаходження шару на платформі 1D при стабілізації.

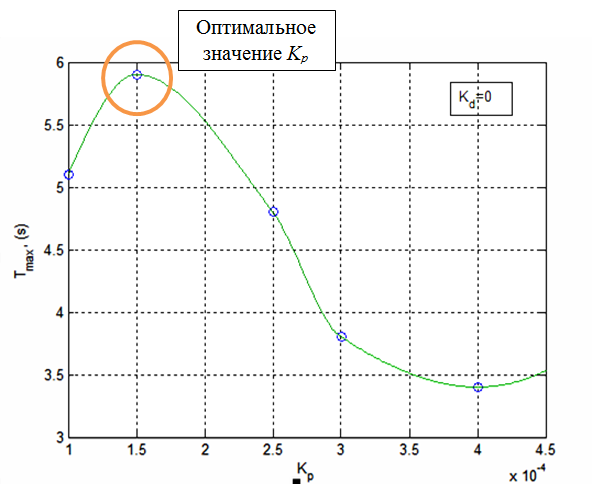
Рисунок 4 - Максимальна тривалість перебування шару на платформі 1D в залежності від kP

Рисунок 4 – Максимальна тривалість перебування шару на платформі 1D в залежності від kP

За отриманими результатами, можна зробити висновок, що максимальної тривалості перебування шару на балансирі відповідає kP = 0,00015. Отримані результати симулювання представлені на рис. 5.

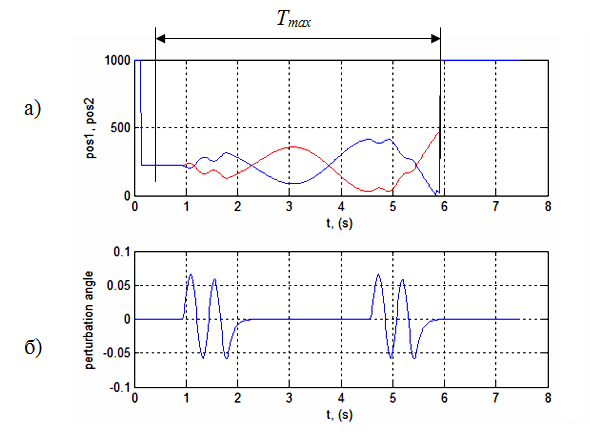
Рисунок 5 - Результати моделювання (kP = 0,00015; kD = 0): a) максимальна тривалість перебування кульки на платформі 1D, б) зовнішні збурення

Рисунок 5 – Результати моделювання (kP = 0,00015; kD = 0): a) максимальна тривалість перебування кульки на платформі 1D, б) зовнішні збурення

Далі, знаходимо значення коефіцієнта kD, відповідно оптимальному значенню kP = 0,00015. Критерій вибору – максимальний час (Tstab) стабілізації шару. Результати представлені на рис. 6.

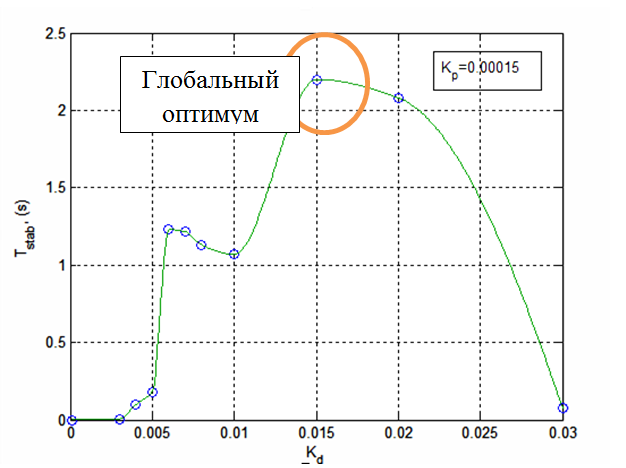
Рисунок 6 - Максимальний час (Tstab) стабілізації шару в залежності від т kD

Рисунок 6 – Максимальний час (Tstab) стабілізації шару в залежності від kD

На рис.6 можна бачити локальний оптимум відповідний Tstab = 1,23 при kD = 0,006 006 і глобальний оптимум, відповідний Tstab = 2,2 при kD = 0,015. При локальному оптимумі система стабілізації поводиться гірше, ніж при глобальному оптимумі (див. рис. 8 та 9 для порівняння).

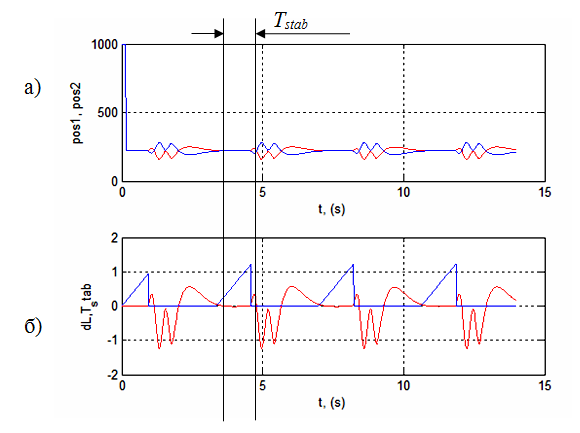
Рисунок 7 - Результати симулювання при локальному оптимумі (kD = 0,006; kP = 0,00015): a) стабілізація; б) положення шару (dL) щодо центру балансира; максимальний час (Tstab) стабілізації шару

Рисунок 7 – Результати симулювання при локальному оптимумі (kD = 0,006; kР = 0,00015): a) стабілізація; б) положення шару (dL) одо центру балансира; максимальний час (Tstab) стабілізації шару

Рисунок 8 - Результати симулювання при глобальному оптимумі (kD = 0,015; kP = 0,00015): a) стабілізація; б) зміщення шару (dL) щодо центру балансира; максимальний час (Tstab) стабілізації шару

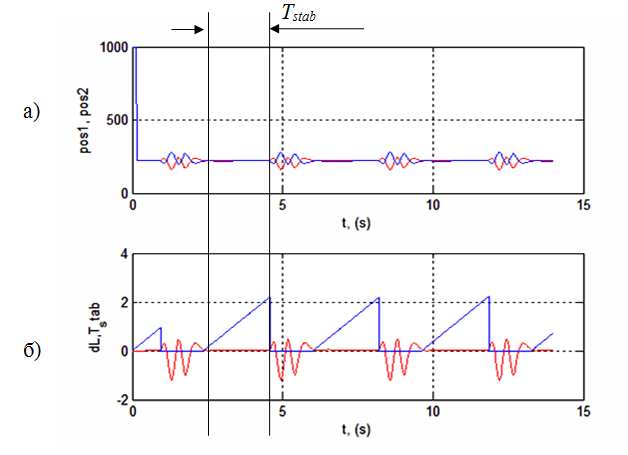
Рисунок 8 – Результати симулювання при глобальному оптимумі (kD = 0,015; kР = 0,00015): a) стабілізація; б) зміщення шару (dL) щодо центру балансира; максимальний час (Tstab) стабілізації шару

Друга ітерація алгоритму вибору коефіцієнта PD регулятора: приймаємо kD = 0,015 і змінюємо значення коефіцієнта kP.

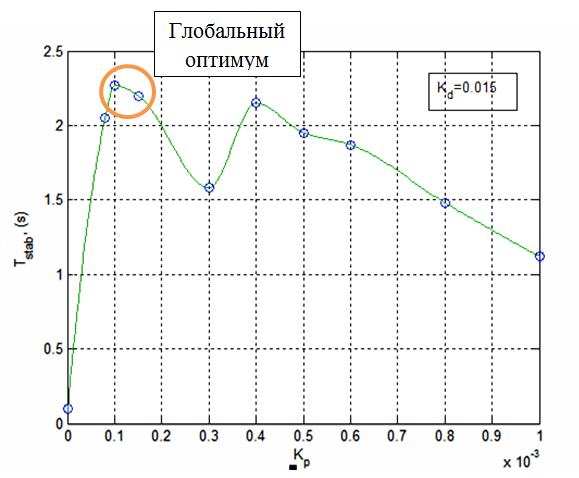
Рисунок 9 –Результати налагодження коефіцієнта kP (kD=0,015)

Рисунок 9 – Результати налагодження коефіцієнта kP (kD = 0,015)

При налагодженні коефіцієнтів так само можна спостерігати два оптимума: локальний оптимум – Tstab = 2,15 при kP = 0,0004 та локальний оптимум – Tstab = 2,27 при kP = 0,0001.

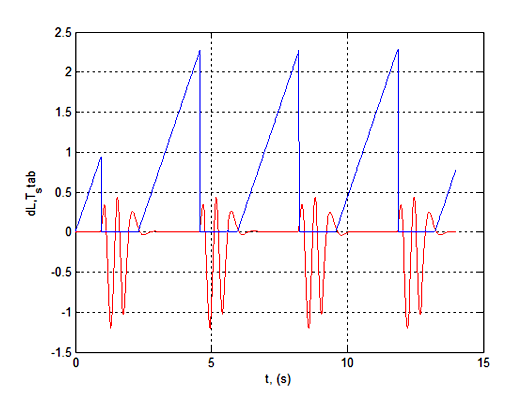
Рисунок 10 – Зміщення шару (dL) щодо центру балансира і максимальний час (Tstab) знаходження шару в стабілізації для оптимальних значень коефіцієнтів kP і kD (kP = 0,0001; kD = 0,015).

Рисунок 10 – Зміщення шару (dL) щодо центру балансира і максимальний час (Tstab) знаходження шару в стабілізації для оптимальних значень коефіцієнтів kP и kD (kP = 0,0001; kD = 0,015)

Для перевірки правильності системи „балансир та шар”, змодельованої в Webots, моделюємо цю ж систему в Simulink на основі рівнянь (1)-(4).

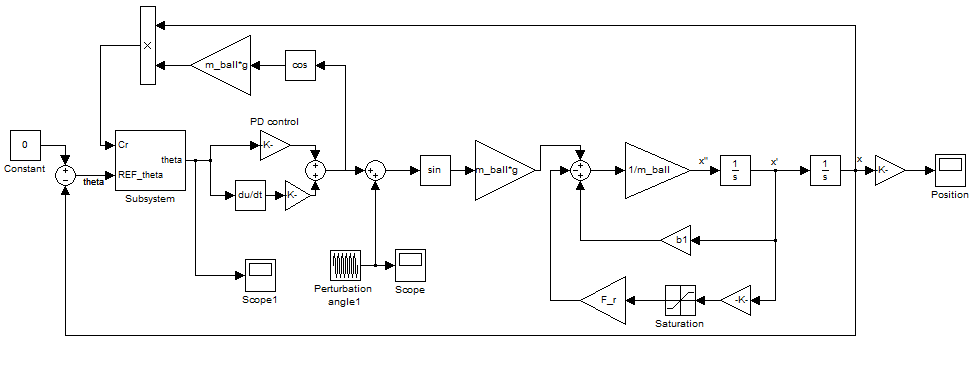
Рисунок 11 – Модель системи Simulink „балансир та шар”

Рисунок 11 – Модель системи Simulink „балансир та шар”

Результати моделювання наведені на рис. 12.

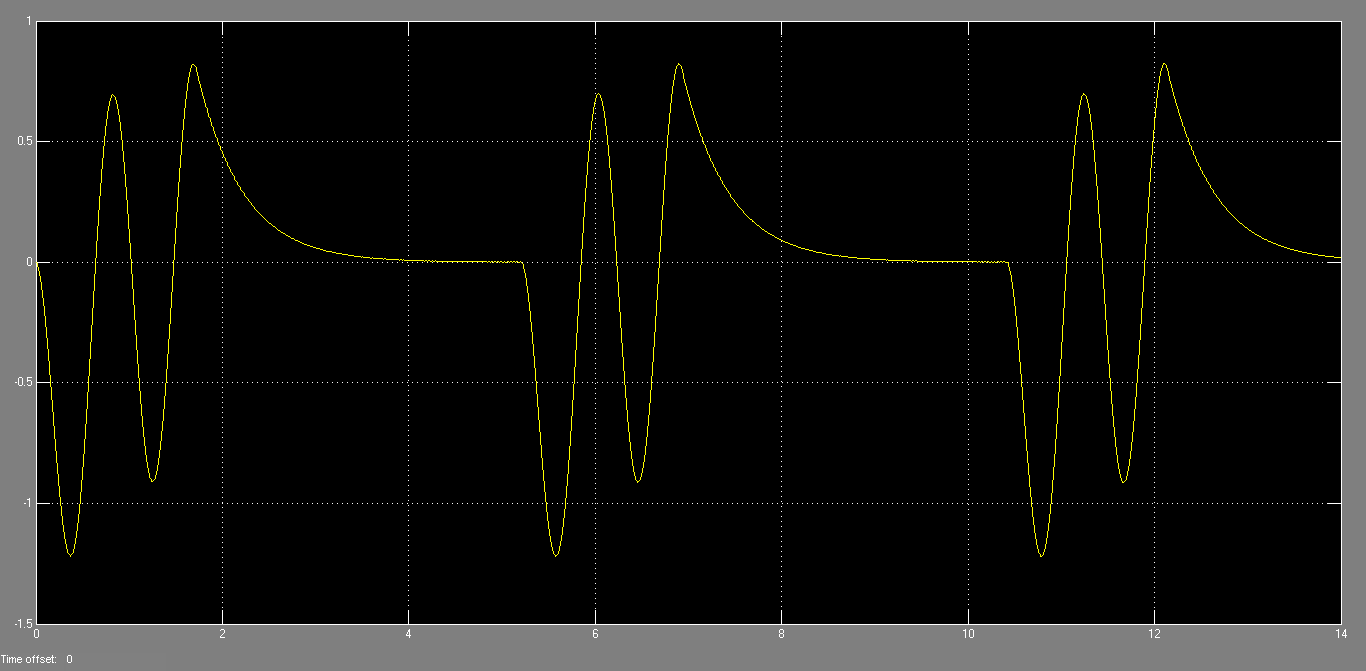
Рисунок 12 - Зміщення шару щодо центру балансира

Рисунок 12 – Зміщення шару щодо центру балансира

Результати, отримані в Simulink дещо відрізняються від результатів, отриманих в Webots. Це може бути пояснено тим, що в Webots для опису фізичних властивостей шару ми можемо задавати такі параметри як щільність, пружність, кулоновское тертя, сила залежного ковзання, в той час як в Simulink ми враховуємо тільки масу і тертя шару

5. Створення експериментального зразка моторизованої площини балансира 1D

Анімація: 7 кадрів, 5 повторень, тривалість кожного кадру - 120 мс, 298 Кб

Рисунок 13 – Експериментальна установка моторизованого балансира 1D: 1 – датчики відстані; 2 – мікродвигун Maxon (двигун, редуктор, датчик кутового положення); 3 – контролер двигуна Maxon EPOS 24/1

Використовуємо переваги сучасного середовища графічного програмування LabView, для графічного програмування завдання автоматизації наукового експерименту: розробки і тестування алгоритмів управління, обробки та аналізу сигналів датчиків, управління двигуном за допомогою контролера Maxon EPOS 24/1, створення інтерфейсу користувача та відображення даних.

Висновки

Моделювання широко використовується при вирішенні різних технічних і наукових проблем. Застосовуються складні інструменти моделювання для точного обліку процесів, що протікають в електромеханічних системах. Моделювання в програмному забезпеченні WebotsTM системи „балансир та шар” дозволило нам перевірити запропонований алгоритм управління, визначити оптимальні коефіцієнти простого ПД-регулятора. Встановлено, що параметри системи управління можуть бути визначені після двох ітерацій роботи моделі. Моделювання цієї ж системи в Simulink дозволило нам перевірити отримані результати і переконатися в їх достовірності.

Подальша робота передбачає розвиток методів біологічно-подібного управління та експериментальні дослідження на розробленій фізичній моделі об'єкта.

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

Перелік посилань

  1. Yu W. Nonlinear PD regulation for ball and beam system // International Journal of Electrical Engineering Education. – Vol. 46, No.1. – 2009. – P. 59-73.
  2. Hamed B. Application of a LabVIEW for Real-Time Control of Ball and Beam System // IACSIT International Journal of Engineering and Technology. – Vol. 2, No.4. – 2010. – P. 401-407.
  3. Marton L., Hodel A.S., Lantos B., Hung J.Y. Underactuated Robot Control: Comparing LQR, Subspace Stabilization, and Combined Error Metric Approaches // IEEE Transactions on Industrial Electronics. – Vol. 55, no.10. – 2008. – Р. 3724-3730.
  4. Bryson A.E., Ho Y.G. Applied Optimal Control // N.Y: Hemisphere, 1975.
  5. Huang J., Lin C.F. Robust nonlinear control of the ball and beam system // Proceedings of the American Control Conference, 1995. – Vol. 1. – P. 306-310.
  6. Almutairi N.B., Zribi M. On the sliding mode control of a Ball on a Beam system // Springer Tracts in Nonlinear Dynamics, 2009. – Vol. 59, Num. 1-2. – 2009. – P. 221-238.
  7. Guo Y., Hill D.J., Jiang Z.P. Global nonlinear control of the ball and beam system // Proceedings of the 35th IEEE Conference on Decision and Control. – Vol. 3. – 11-13 Dec,1996. – P. 2818-2823.
  8. YI J., Yubazaki N., Hirota K. Stabilization Control of Ball and Beam Systems // International Conference IFSA World Congress and 20th NAFIPS, 2001, Joint 9th Vol. 4. – P. 2229-2234.
  9. Eaton P.H., Prokhorov D.V., Wunsch D.C. Neurocontroller Alternatives for Fuzzy Ball and Beam Systems with Nonuniform Nonlinear Friction // IEEE Transactions of the Neural Networks, March 2000. – Vol. 11, No 2. – P. 423-435.
  10. Hauser J., Sastry S., Kokotovic P. Nonlinear control via approximate input-output linearization: the ball and beam example // IEEE Transactions on Automatic Control.– Vol. 37. – Issue: 3. – March 1992. – P. 392-398.
  11. Tomlin C.J., Sastry S. Switching through singularities // Proceedings of the 36th IEEE Conference on Decision and Control. – Vol. 1. – 1997. – P. 1-6.
  12. Lai M.C., Chien C.C., Cheng C.Y., Xu Z., Mang Y. Nonlinear Tracking Control Via Approximate Backstepping // Proceedings of the American Control Conference, 1994. – Vol. 2. – 29 Jun-1 Jul. – 1994. – P. 1339-1343.
  13. Dale S., Dragomir T.L. Interpolative-type control solution for a Ball and Beam system // CEAI, Vol. 8, No. 3. – 2006. – P. 3-14.
  14. Marra M.A., Boling B.E., Walcott B.L. Genetic control of a ball-beam system // Proceedings of the 1996 IEEE International Conference on Control Applications. – 1996. – P. 608-613.
  15. Simmons A.T., Hung J.Y. Hybrid Control of Systems with Poorly Defined Relative Degree: The Ball on Beam Example // 30th Annual Conference of IEEE Industrial Electronics Society, 2004. – Vol 3. – P. 2436-2440.
  16. Barbu C., Sepulchre R., Lin W., Kokotovic P.V. Global Asymptotic Stabilization of the Ball-and-Beam System // Proceedings of the 36th IEEE Conference on Decision and Control. – 1997. – P. 2351-2355.
  17. Petrovic I., Brezak M., Cupec R. Machine vision based control of the ball and beam // 7th International Workshop Advanced Motion Control. – 2002. – P. 573-577.
  18. Naz S.A., Katebi R., Balbis L. Implementation of Kalman Filter on Ball And Beam Experiment Using Labview // International Conference Control 2006, Glasgow.
  19. Michel O. Webots: Professional Mobile Robot Simulation // International Journal of Advanced Robotic Systems. – Vol. 1, Num. 1, – P. 39-42.
  20. http://www.labview.ru/labview/what_is_labview/index.php