Aperçu
Sommaire
- Introduction
- 1. Actualité de la thèse
- 2. Buts et problèmes de la recherche, les résultats planifiés
- 3. Synthèse des recherches et des élaborations
- 3.1 Synthèse de la bibliographie internationale
- 3.2 Synthèse de la bibliographie nationale et locale
- 4. Modélisation d'ordinateur du neurone.
- Conclusion
- Bibliographie
Introduction
Aujourd'hui, le développement de la robotique est à un niveau élevé. Les robots sont utilisés dans l'industrie manufacturière, en tout ou en partie ils remplacent de l'homme, ils effectuent des opérations techniques de différente complexité. Ils sont également largement utilisés dans la vie quotidienne, aidant les personnes. C'est, de plus en plus robots interagissent avec les personnes. L'interaction entre la personne et le robot à cinématique complexe dépend du système de commande du robot. Pour créer ce système, les connaissances informatiques et techniques ne sont pas suffisants. Par conséquent, de nombreux scientifiques se tournent vers paradigmes biologiques fondamentales, c-à-d ils utilisent les connaissances des sciences humanitaires.
Dans ce projet, on recherche le système de contrôle de la compliance des articulations d'un robot manipulateur Katana. A la base des articulations du robot il y a système moteur-réducteur du type Harmonique Drive. A cause de la présence ce système il y a les élasticités dans les articulation du robot. Le contrôle de ce système à l’aide du régulateur PID est largement utilisé.
1. Actualité de la thèse
La nouveauté de ce travail consiste en amélioration du contrôle de la compliance des robots électromécaniques grâce à l'utilisation d'oscillateurs neuronaux, que permet augmenter l'adaptation du système par raport à la variation des paramètres et des conditions d'exploitation, ce qui est particulièrement important pour le cas de l'interaction entre le robot et l’humain. Encore on éstime la fiabilité du système de commande du robot, on propose l’amélioration de ce système.
2. Buts et problèmes de la recherche, les résultats planifiés
L’objective de ce travail est l’amélioration du contrôle de la compliance du robot électromécanique en interaction physique avec l’humain.
Les problèmes principales, qui sont resolus dans le travail:
- Principes du contrôle de la compliance.
- Utilisation de réducteurs d'onde dans la robotique.
- Modèle mathématique du robot, en tenant compte des élasticités de transmission et la cinématique des articulations de robot.
- Modélisation mathématique des oscillateurs neuronaux bioinspirés.
- Estimation de la fiabilité du système de commande du robot Katana.
- Recherches expérimentales avec du robot Katana.
3. Synthèse des recherches et des élaborations
3.1 Synthèse de la bibliographie internationale
Pour le robot Katana on utlise le moteur à courant continu et le réducteur Harmonic Drive. Le réducteur Harmonic Drive consiste en trois parties. Ces sont le générateur d’ondes, la partie flexible et la partie circulaire [1].

Figure 1 – Composants d’Harmonic Drive
Les avantages d’HD sont: un grand couple d’entrainement, la construction concentrique, la légèreté, la compacité, l’absence d’entrefer, haute efficacité, la réversibilité.
Grace à ces avantages les réducteurs Harmonic Drive sont très populaires aux manipulateurs industriels. Toutefois, ils ont des inconvénients: la rigidité non-linéaire, les vibrations de la résonance, le frottement des non-linéarités [1]. Mais les manipulateurs directs ont l’arbre sortie du moteur, qui est relié directement de sortie du lien. Ainsi donc les effets indésirables de la transmission se minimisent, par exemple, l'entrefer, qui est difficile à modéliser. Très bon contrôle du moment de lien est possible à commande direct du manipulateur [2].
Notons que les effets de frottement en HD sont complexes et difficiles à modéliser.
Le comportement de la transmission Harmonic Drive complique l’usage des modèles dynamiques pour le contrôle de l'impédance [2].
Il y a quelques problèmes du contrôle de la compliance du robot.
Au cours des quinze dernières années une grande quantité de la recherche a été porté sur le contrôle d’élasticité des liens des robots. A partir de méthodes de contrôle développées pour rigide manipulateurs, il ya des résultats très puissants théoriques concernant le contrôle des manipulateurs avec des élasticités en articulations. Il s'agit notamment de perturbation singulière (ang. singular perturbation) et multiple intégrante (ang. integral manifold), la linéarisation à rétroaction; (ang. feedback linearization), la linéarisation dynamique à rétroaction; (ang. dynamic feedback linearization), méthodes adaptives de contrôle [3].
En fait, l'élasticité des transmissions mécaniques induit des erreurs de position du robot à cause de la deformation statique sur l’influence de la gravité. En outre, il peut devenir une source d'instabilité en cas d'interaction entre le robot et l'environnement ou lorsque la rétroaction est basée sur la mesure des variables de lien uniquement (De Luca & Tomei, 1996) [4].
On suppose que l'élasticité se concentre à "n" articulations de robot n et le nombre des variables de Lagrangian configuration en dynamique du robot est doublé par rapport au robot rigide, menant à grande quantité "n" moteurs et "n" articulations du second ordre équations non linéaires [4].
Contrôle de l'impédance cartésienne, comme une approche particulière du problème de contrôle de la compliance du mouvement, peut évidemment être vu comme l'une des méthodes principales de contrôle moderne du robot. L’objectif fondamental de contrôle de l'impédance dans le sens le plus général est l’obtention de la relation dynamique desirée entre les forces externes et les mouvements du robot . Cependant, dans de nombreux les applications robotiques ce comportement dynamique est spécifié en point de vue de rigidité et des matrices d'amortissemens par rapport de certains Coordonnées cartésiennes [5].
La proportionnelle, intégrale et dérivée (PID) algorithme reste l'approche la plus populaire pour les contrôle des processus industriels en dépit des progrès continuels dans contrôler la théorie. Ce n'est pas seulement due à la structure simple, qui est conceptuellement facile à comprendre et, ce qui rend la syntonisation manuelle est possible, mais aussi à la fait que l'algorithme fournit des performances approprié dans la grande majorité des applications. Cependant, pour une variété des raisons réglage optimal des gains est difficile et comme conséquence, de nombreuses techniques de conception d'un PID été développés dans la littérature (voir, par exemple, Astrom & Hagglund, 1984; Zhuang & Atherton, 1993; Daley & Liu, 1998; Liu, Dixon & Daley, 1998; McCormack & Godfrey, 1998) [6].
La plupart des règles de réglage du PID développé dans les 50 derniéres années d'utilisation de fréquence de réponse des méthodes. Les exemples incluent, règle (Ziegler & Nichols, 1942), symétrique règle optimale (Kessler, 1958; Voda & Landou, 1995), règle complémentaire Ziegler, Nichols (Mantz & Tacconi, 1989), certains-dépassement règle (Seborg, Edgar) [6].
Traditionnellement, la conception du contrôle de robot manipulateur peut être réalisé comme le tuning d'un PD ou compensateur PID au niveau de chaque moteur dans les liens du manipulateur. Fondamentalement le PD contrôleur est la position et la vitesse de rétroaction, qui a bonnes propriétés en boucle fermée lorsqu'elle est appliquée à un double intégrateur de système [7].
L’article [8] montre la possibilité de modélisation du système musculaire non linéaire. Pour créer le modèle on utilise PID régulateur et le moteur à courant continu. Le moteur et PID régulateur sont connectés en contour fermé. On peut changer les paramètres de PID Kc, Ti, Td. Le perceptron multicouche (réseau neurone artificiel) est utilisé pour régler les paramètres du PID. On montre, que la sortie du moteur donne le comportement, qui se ressemble du comportement d’homme.
Dans ce travail on utilise le modèle d'un neurone de Rowat-Selverston. Les scientists américains Rowat et Selverston a présenté un modèle d'approximation d'un neurone pour lequel a identifié deux groupes de courants: un "rapide" et "lent". Les courants sont déterminés par des équations différentielles de premier ordre. Courant rapide de l'équation (1), et courant lent – de l'équation (2) [9]:
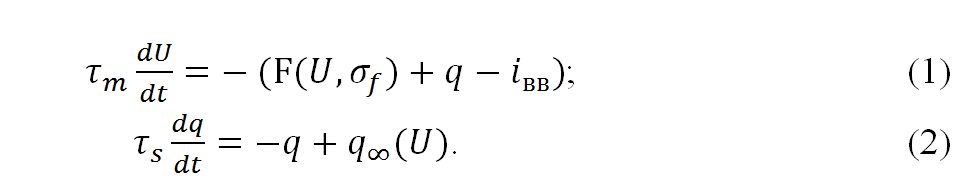
où τm < τs, τm – constante de temps de la membrane neuronale; τs – constante de temps d'activation lente des courants;
iвв – le courant introduit; U – la tension de la membrane; q – le courant lent; U et q sont les valeurs variables;
F(U,σf) – la caractéristique courant-tension non-linéaire pour le courant rapide, qui est définie par l’équation (3):
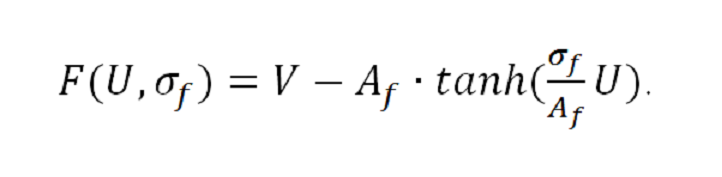
La fonction F(U,σf) est un partie fondamental du modèle de Rowat-Selverston, parce que elle dépend de la valeur du coefficient du renforcement à courant σf provoque le comportement différent de l'oscillateur [10,11] (oscillatoire amorti, potentiel ou oscillatoire sans amortissement). La dépendance de F(U,σf) peut être linéaire et non-linéaire.
3.2 Synthèse de la bibliographie nationale et locale
Pour la recherche on utilise le robot manipulateur avec six degrés de liberté Katana de la fabricant suisse Neuronics. Vue générale de la configuration de la Katana manipulateur avec différents types d’organ de levage de la fig. 1. Le manipulateur a six degrés de liberté, chaque artiqulation de la manipulateur tourne avec la commande électrique à courant continu, qui a monté avec le réducteur d’onde Harmonic Drive. Ce réducteur est la raison pour laquelle il y a les élasticités qui interfèrent avec le fonctionnement normal du robot. Les moteurs sont alimentés par réglage individuel PWM-convertisseurs. Le système du contrôle est fermée sur la position et/ou la vitesse du moteur. La commande centralisée peut être réaliser à partir d’ordinateur ou à l’aide de PLC-contrôleur [12].
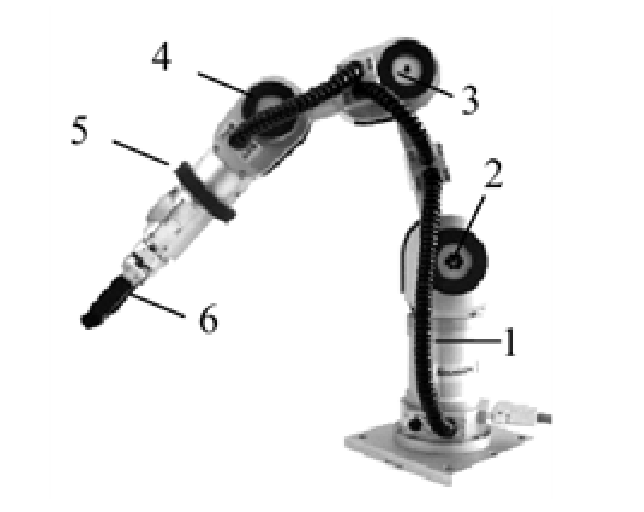
Figure 2 - Vue générale du robot manipulateur Katana- 6M180:
1 - 6 - degrés de liberté:
Le chargement maximale recommandée d’organ de travail du robot est 500 g, ce qui, compte tenu des taux élevés de vitesse et de précision, peut être utilisé comme un assistant robot interactif dans l'interaction de la personne et de résoudre plusieurs problèmes pratiques de l'automatisation du processus technique (micro-soudage, la manipulation d'objets sur la ligne de transport etc) [12].
Dans les articles [13,14] on est élaboré la langage de la commande du robot pour la partie du complexe programmatique du contrôle du manipulateur fabriqant Neuronics AG. On est réalisé l’interface programmatique sur la base KNI. On est cré é pour la famille des robots Neuronics AG en simulateur Webots et au équipement réel pour Katana.
4. Modélisation d'ordinateur du neurone
D'après les équations (1) et (2) on est composé un modèle dans Simulink MATLAB (cf. fig. 2), où pour une solution de l'équation rapide, nous utilisons la formule (3). Les valeurs des constantes prendre les valeurs suivantes [9] : Af = 1; σf =3; τs = 1; τm = 1/20.
Composons le description de modèle d'oscillateur sur la langage de script Matlab. Utillisons la method d'intégration numérique avec le contrôle de le pas ode45 [15]:

Animation: 7 cadres, durée de chaque cadre - 70 ms, 165 Kb
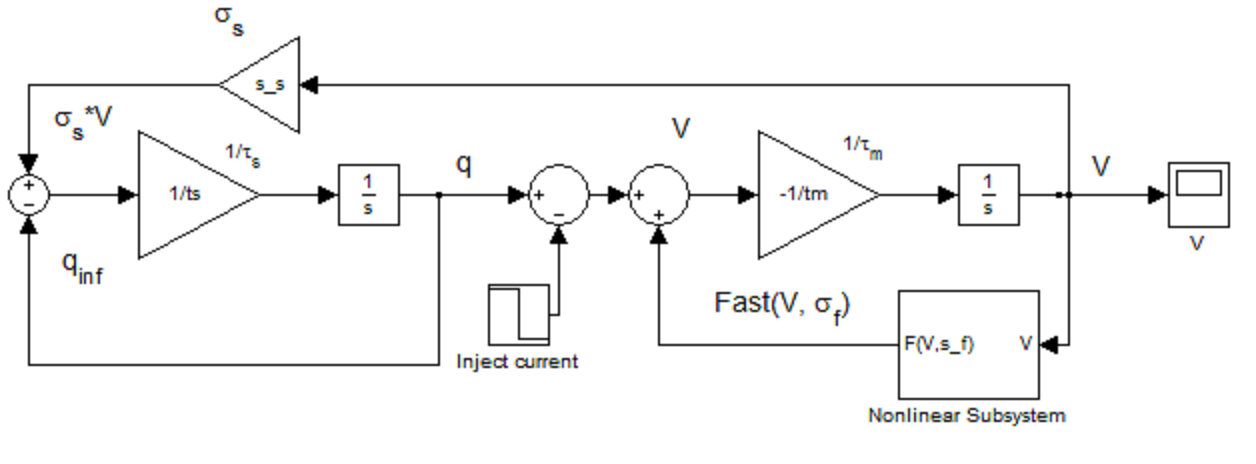
Figure 3 – Réalisation d’oscillator de Rowat-Selverston l’aide dàe SIMULINK
Analyse des résultats de la simulation
Compte tenue des renseignements ci-dessus pour la précision de la simulation, nous avons obtenu les réactions de l'oscillateur Rowat- Selverston sur les actions d'entrée typique. Modèle a été utilisé (cf. fig. 3). Les résultats sont présentés à la (cf. fig. 5) [15].
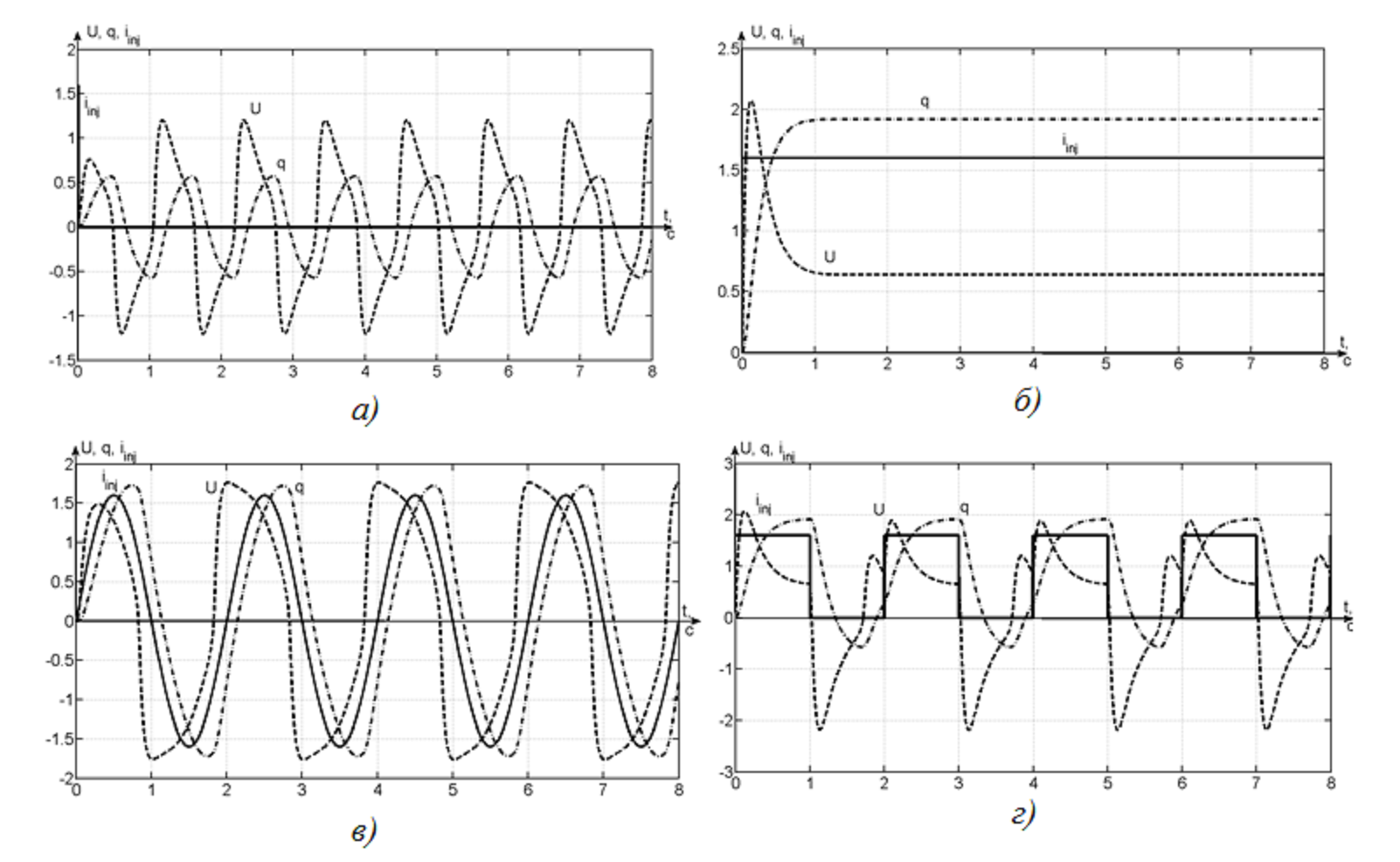
Figure 4 - Réaction d'oscillateur pour les actions d'entrée différents:
a) un impulsion; b) un saut; c) un sinus (T = 0,5 s); d) un méandre (T = 0,5 s).
En résultat de la simulation ont été obtenues oscillations de diverses natures: a) anharmonique d’une fréquence 1,11 Hz; b) apériodique avec constante du temps de 0,25 s; c) quasi-harmonique à la source sinusoidale; d) anharmonique aux signals rectangulaires.
Les oscillations au-dessus caractérisent les régimes principaux de fonctionnement de l'oscillateur Rowat-Selverston [16], ils affichent ses propriétés de la génération des signaux apériodiques et périodiques. Dans ce cas, la synchronisation avec un apport périodique (onde sinusoidale,un méandre) n'est pas typique pour les systèmes biologiques où des impulsions discrètes du courant contrôlent l’inflammation neurone (comme dans la fig. 4.a).
Le modèle simple consideré d'un oscillateur artificielle ne prend pas en compte les propriétés individuelles de son homologue biologique, qui est le neurone du générateur central de motions. Par exemple, il ne tient pas compte des retards qui affectent la dynamique du système. Entrées de générer immédiatement un signal de sortie. Et, plus important encore, un oscillateur séparé ne compte tenue pas les effets des fonctions biologiques de la fonction de synchronisation des neurones, que certains chercheurs considèrent comme essentiels. Ce dernier phénomène est souvent utilisé pour générer les mouvements rythmiques de robots anthropomorphes, puisque il modèle pour le processus naturel de l'interaction humaine avec l'environnement (gestes, actions répétitives, etc.) Toutefois, un certain nombre de documents indique que la propriété est associée à une auto-synchronisation d'une paire d'oscillateurs Rowat-Silverston qui est le cas le plus typique dans les systèmes biologiques. Ce sera l'objet de nos recherches futures.
Conclusions
Dans ce travail on décrit la dynamique des liens internes de robots élastiques avec la cinématique complexe. Tenant compte de l'élasticité des articulations internes est important. Il influe sur la qualité des interactions d'un robot avec son environnement, en particulier lors de l'interaction avec les humains. On peut évaluer ce phénomène lors d'une approche classique PID règlement est employé. Dans le type considéré de robots élasticité résulte principalement de la réducteur Harmonic Drive. L'approche d'inspiration biologique est nécessaire pour contrôler l'interaction avec un humain dans un cadre naturel, de façon plus perspicace. Ainsi, on a étudié les propriétés d’oscillateur Rowat-Selverston. On planifie l’utilisation de cet oscillateur pour l’amélioration du contrôle de la compliance des robots électromécaniques.
Maintenant le projet de master n'est pas préparé finalement. La date d'achèvement définitif est le decembre 2012.
Bibliographie
- Taghirad H.D., Bélanger P.R. Modeling and parameter identification of Harmonic Drive systems // Journal of Dynamic Systems, Measurements, and Control. – 22 p. [электронный ресурс]. – Режим доступа:
http://saba.kntu.ac.ir/eecd... - Tischler N. Stiffness control of robot manipulator // Proceedings 2001 ICRA IEEE International Conference on Robotics and Automation Cat No01CH37164 (2001), p. 3042 – 3046 [электронный ресурс]. – Режим доступа: http://masters.donntu.edu...
- Schaffer A. A., Hirzinger G. State feedback controller for flexible robots: A globally stable approach implemented on DLR’s light-weight robots // Robotics and Automation, 2007 IEEE International conference, 2007, p. 3824 – 3830 [электронный ресурс]. – Режим доступа: http://www.morpha.de/morpha_page...
- Luca A. D., Siciliano B., Zollo L. PD control with on-line gravity compensation for robots with elastic joints //Automatica 41(2005), 1809 – 1819.
- Ott C., Schaffer A. A., Kugi A. – A passivity based cartesian impedance controller for flexible joint robots – Part 1: Torque feedback and gravity compensation [электронный ресурс]. – Режим доступа: https://www.google.com...
- Liu G.P., Daley S. Optimal-tuning PID control for industrial systems // Control Engineering Practice 9 (2001)
p. 1185 - 1194 [электронный ресурс]. – Режим доступа: http://www.sciencedirect.com... - Bruno S., Oussama K. – Handbook of Robotics, 2008, LX, p. 7 – 9 [электронный ресурс]. – Режим доступа: http://books.google.com.ua/books...
- Serhan H., Nasr C. G., Henaff P. – Muscle emulation with DC motor and neural networks for biped robots // Int J Neural Syst. 2010 Aug; 20(4): 341 – 53.
- Rowat P.F., Selverston A.I. Oscillatory mechanisms in pairs of neurons connected with fast inhibitory synapses // Journal of Computational Neuroscience 4. – Kluwer Academic Publishers, 1997. – 25 p. [электронный ресурс]. – Режим доступа: http://crayfish.ucsd...
- Кузнецов А.П., Кузнецов С.П., Рыскин Н.М. Нелинейные колебания. Учеб. пособие для вузов. – М.: Издательство физико-математической литературы, 2002. – 292 с. [электронный ресурс]. – Режим доступа: http://www.sgtnd.narod.ru...
- Кириллов С.Ю., Клиньшов В.В. Исследование динамических режимов модели нейрона с последеполяризацией // Труды научной конференции по радиофизике. – ННГУ, 2007. – 86 с. [электронный ресурс]. – Режим доступа: https://www.google.com/url...
- Мельник А.А., Хоменко В.Н., Плис П.С., П. Энафф, Борисенко В. Ф. – Кинематическая модель робота с шестью степенями свободы и возможностью учета зазора в суставах. Научные труды ДонНТУ, 10(180) 2011, 113 – 120 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal...
- Рябченко В.В., Дацун Н.Н. Программно-аппаратный комплекс управления роботами-манипуляторами фирмы Neuronics AG // Материалы 4-й международной научно-технической конференции "Моделирование и компьютерная графика – 2011". Донецк, 5-8 октября 2011 г. С. 295 – 299 [электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080...
- Рябченко В.В., Дацун Н.Н. Использование моделирующей среды для создания программного обеспечения программно-аппаратного комплекса управления роботом-манипулятором семейства Katana фирмы Neuronics AG // Наукові праці Донецького національного технічного університету 14 (188), 2011. – 335 – 339 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal...
- Snegina E., Pougatch A., Khomenko V., Melnyk A., Henaff P., Borysenko V. Practical aspects of Rowat-Selverston
bio-inspired oscillator simulation // Наукові праці Донецького національного технічного університету 11 (186), 2011. – 369 – 373 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal... - Amrollah E., Henaff P. On the role of sensory feedbacks in Rowat–Selverston CPG to improve robot legged locomotion // Frontiers in Neurosciences. Neurorobotics 4, 113, 2010. – 9 p. [электронный ресурс]. – Режим доступа: http://www.ncbi.nlm.nih.gov...
