Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та заплановані результати
- 3. Огляд досліджень та розробок
- 3.1 Огляд міжнародних джерел
- 3.2 Огляд національних і локальних джерел
- 4. Комп'ютерне моделювання нейрона
- Висновки
- Перелік посилань
Вступ
В даний час розвиток робототехніки знаходиться на високому рівні. Роботи використовуються в промисловій індустрії, повністю або частково вони замінюють собою людину, здійснюють технічні операції різної складності. Вони також широко використовуються в повсякденному житті, допомагаючи людям. Тобто роботи все більше взаємодіють з людьми. Взаємодія між людиною і роботом зі складною кінематикою залежить від системи управління роботом. Щоб створити цю систему, комп'ютерних і технічних знань недостатньо. Внаслідок цього, багато дослідників звертаються до фундаментальних біологічних знань.
Одна з властивостей біомеханічних систем – це податливість під впливом зовнішніх сил. У цьому проекті досліджується система управління піддатливістю робота-маніпулятора Катана. В основі ланок робота знаходиться система двигун-редуктор типу Harmonic Drive. Наявність цієї системи викликає появу пружності в ланках робота. Широко поширене управління системою Harmonic Drive за допомогою ПІД-регулятора (англ. PID).
1. Актуальність теми
Новизна роботи полягає у вдосконаленні системи управління піддатливістю електромеханічних роботів за рахунок застосування біологічно подібних контролерів (нелінійних осциляторів), що дозволяє підвищити адаптивність системи по відношенню до варіації її параметрів і умов роботи, що особливо важливо для випадку взаємодії робота з людиною. Оцінюється надійність робототехнічної системи, пропонується поліпшення цієї системи.
2. Мета і задачі дослідження та заплановані результати
Метою даної роботи є удосконалення системи управління піддатливістю електромеханічних роботів зі складною кінематикою при фізичному взаємодії з людиною і оцінка її надійності.
Основні питання, які вирішуються в роботі:
- Принципи управління податливістю.
- Застосування хвильових редукторів в робототехніці.
- Математична модель робота з урахуванням пружності передач і кінематики ланок робота.
- Математичне моделювання біологічно подібних нейронних осциляторів.
- Оцінка надійності системи управління робота Катана.
- Експериментальні дослідження з роботом.
3. Огляд досліджень та розробок
3.1 Огляд міжнародних джерел
У ланках робота Катана встановлені двигуни постійного струму й редуктори типу Harmonic Drive. Редуктор Harmonic Drive складається з трьох частин: хвильовий генератор, гнучка частина із зовнішніми зубцями і кругова частина з внутрішніми зубцями [1].

Рисунок 1 – Компоненти редуктора Harmonic Drive
Переваги редуктора: великий крутний момент, концентрична конструкція, легкість, компактність, відсутність зазору, висока ефективність, зворотна керованість.
Завдяки своїм перевагам редуктори Harmonic Drive дуже популярні в промислових маніпуляторах. Але вони мають і недоліки: висока пружність, резонансні вібрації, тертя [1]. У маніпуляторах з безпосереднім приводом вихідний вал двигуна з'єднується безпосередньо з виходом ланки, і таким чином, зводяться до мінімуму небажані ефекти передачі, наприклад, зазор, який складно змоделювати. Також при безпосередньому приводі маніпулятора є можливим досить хороший контроль моменту ланки [2].
Необхідно відзначити, що тертя в редукторі є складним для комп'ютерного моделювання.
Ще одним недоліком редуктора гармонік Драйв є те, що динамічна поведінка передачі ускладнюється при бажанні керувати механічним імпедансом [2].
Існує декілька проблем при управлінні податливістю робота.
В останні 15 років велика кількість досліджень була зосереджена на управлінні пружністю ланок робота. Починаючи з методів управління, розроблених для жорстких частин маніпулятора, є деякі потужні теоретичні результати, що стосуються управління маніпуляторами з пружностями в ланках. До них відносяться сингулярні збурення (англ. singular perturbation) та інтегральне різноманіття (англ. integral manifold), лінеаризація зі зворотним зв'язком (англ. feedback linearization), динамічна лінеаризація зі зворотним зв'язком (dynamic feedback linearization), а також адаптивні методи управління [3].
Насправді, пружність в механічних передачах викликає помилки в положенні робота з причини деформації під дією сили тяжіння. Крім того, вона може стати джерелом нестабільності в разі взаємодії між роботом і навколишнім середовищем, або коли зворотний зв'язок базується на вимірюванні тільки змінних складових ланки (De Luca & Tomei, 1996) [4].
Передбачається, що пружність зосереджена в «n» ланках робота і кількість змінних конфігурації Лагранжа в динаміці робота є подвоєною в порівнянні з жорстким роботом, що призвело до великої кількості «n» двигунів і «n» ланок в нелінійних рівняннях другого порядку [4].
Контроль імпедансу, як один з окремих підходів до проблеми управління піддатливістю руху, очевидно, може бути розглянуто як один з основних методів сучасного управління роботом. Фундаментальною метою контролю імпедансу в найзагальнішому сенсі є отримання бажаного динамічного співвідношення між зовнішніми силами і рухами робота. Тим часом, в численних робототехнічних додатках ця динамічна поведінка визначається з точки зору жорсткості та матриць загасання по відношенню до деяких декартових координат [5].
Пропорційний, інтегральний та диференціальний (ПІД) алгоритм залишається найбільш популярним підходом в управлінні промисловими процесами на протязі розвитку теорії управління. Це пояснюється не тільки простою структурою, яка є простою для розуміння, дозволяє налаштування вручну, але також при використанні алгоритму дає відповідні результати у великій кількості різних областей. Тим не менш, оптимальне визначення коефіцієнтів є складним, і як наслідок, численні концепції управління ПІД-регулюванням знайшли своє відображення в літературі (Astrom & Hagglund, 1984; Zhuang & Atherton, 1993; Daley & Liu, 1998; Liu, Dixon & Daley, 1998; McCormack & Godfrey, 1998) [6].
Більшість правил ПІД-регулювання були розроблені в останні 50 років. Це, наприклад, правило Ziegler & Nichols (Ziegler & Nichols, 1942), оптимальне правило симетрії (Kessler, 1958; Voda & Landou, 1995), додаткове правило Ziegler & Nichols (Mantz & Tacconi, 1989), правило деякого перевищення (Seborg, Edgar) [6].
Традиційно, концепція управління роботом-маніпулятором може здійснюватися простою настройкою ПД або ПІД регулятора на рівні кожного двигуна у ланках маніпулятора. По суті, ПД контролер є положенням і швидкістю зворотного зв'язку, яка утворена замкнутим контуром з хорошими властивостями, коли вона застосовується до системи з подвійним інтегратором [7].
Стаття [8] демонструє можливість комп'ютерного моделювання нелінійної м'язової системи. Використовується ПІД-регулятор і двигун постійного струму. Двигун і ПІД-регулятор з'єднані в замкнутий контур. Можна змінювати параметри ПІД – Kc, Ti, Td. Багатошаровий персептрон (штучна нейронна мережа) використовується для регулювання параметрів ПІД. Показано, що на виході ланки отримана поведінка, еквівалентна поведінці мускула людини.
У магістерській роботі з метою контролю пружних ланок робота використовується модель біологічного нейрона Ровата-Сельверстона. Американські вчені Роват і Сільверстон в 1997 р. представили аппроксимуючу модель нейрона, для якого визначено дві групи струмів: «швидкий» і «повільний». Струми визначаються диференціальними рівняннями першого порядку. Швидкий струм рівнянням (1), а повільний - рівнянням (2) [9]:
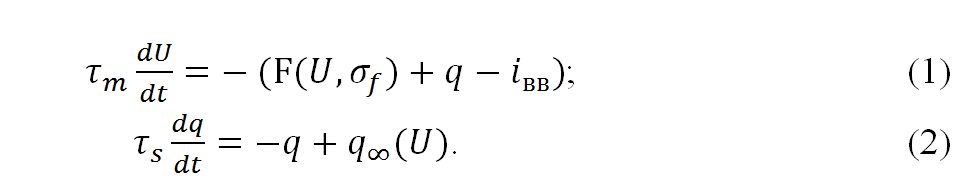
де τm < τs, τm – стала часу нейронної мембрани; τs – стала часу повільної активації струмів; iвв – введений струм; U – напруга мембрани; q – повільний струм; U і q – змінні величини; F(U, σf) - нелінійна вольт-амперна характеристика для швидкого струму, яка визначається виразом:
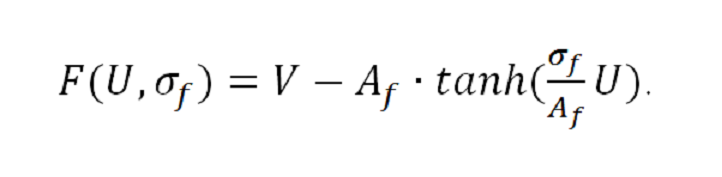
Функція F(U,σf) є фундаментальною частиною моделі Ровата-Сильверстона, оскільки вона, залежно від значення коефіцієнта посилення по струму σf, викликає різну поведінку осцилятора [10,11] (загасаюча коливальна, потенційна або коливальна без загасання). Залежність F(U,σf) може мати лінійний і нелінійний характер.
3.2 Огляд національних і локальних джерел
Для дослідження використовується робот-маніпулятор Катана з шістьма ступенями свободи швейцарського виробника Neuronics. Загальний вид конфігурації маніпулятора Katana наведено на рис. 2. Маніпулятор має шість ступенів свободи, кожне зчленування маніпулятора – обертальне з електричним приводом постійного струму, соосно монтується з хвильовим редуктором Harmonic Drive. Двигуни живляться від індивідуально керованих ШІМ-перетворювачів. Система регулювання замкнута по положенню і / або за швидкістю двигуна. Управління електромеханічними системами окремих суглобів реалізовано на базі локального контролера робота, централізоване управління може здійснюватися від комп'ютера, або за допомогою PLC-контролера [12].
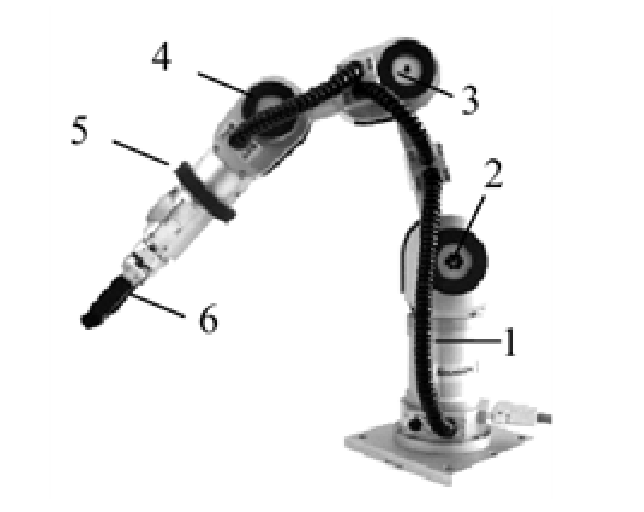
Рисунок 2 – Загальний вид конфігурації робота-маніпулятора Катана-6М180:
1 - 6 - електричні рушії робота
Рекомендоване максимальне завантаження робочого органу робота становить 500 г, що, враховуючи високі показники швидкодії і точності, дозволяє використовувати робот в якості інтерактивного помічника при взаємодії з людиною, а також вирішувати ряд практичних питань автоматизації технологічного процесу (мікрозварювання, маніпуляція об'єктами на конвеєрній лінії) [12].
У статтях [13,14] розроблено програмно-аппаратний комплекс управління роботом-маніпулятором ф. Neuronics AG. Реалізовано програмний інтерфейс на базі KNI. Створено ПІ для семейст роботів ф. Neuronics AG в симуляторі Webots і на реальному обладнанні для Katana.
4. Комп'ютерне моделювання нейрона
Згідно рівнянням (1) і (2) складена модель в Simulink MATLAB (рис. 2), де для вирішення швидкого рівняння використовуємо формулу (3). Значення постійних величин приймаємо наступними [9] : Af = 1; σf = 3;
τs = 1; τm = 1/20.
Складено опис моделі осцилятора на скрипт-мові Matlab. Застосовано метод чисельного інтегрування з автоматичним вибором кроку ode45 [15]:

Анімація: 7 кадрів, тривалість кожного кадру – 70 мс, 165 Кб
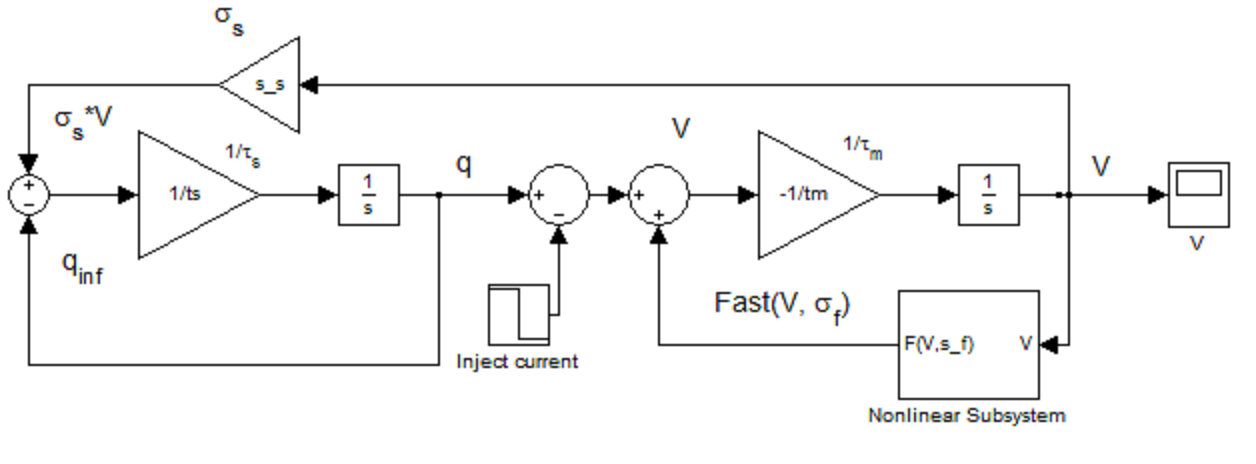
Рисунок 3 – Реалізація осцилятора Ровата-Сильверстона в пакеті Simulink
Аналіз результатів моделювання
З урахуванням вищенаведених відомостей про точність моделювання, нами були отримані реакції осцилятора Ровата-Сильверстона на типові вхідні впливи. Була використана модель рис. 3. Результати наведені на рис. 4 [15].
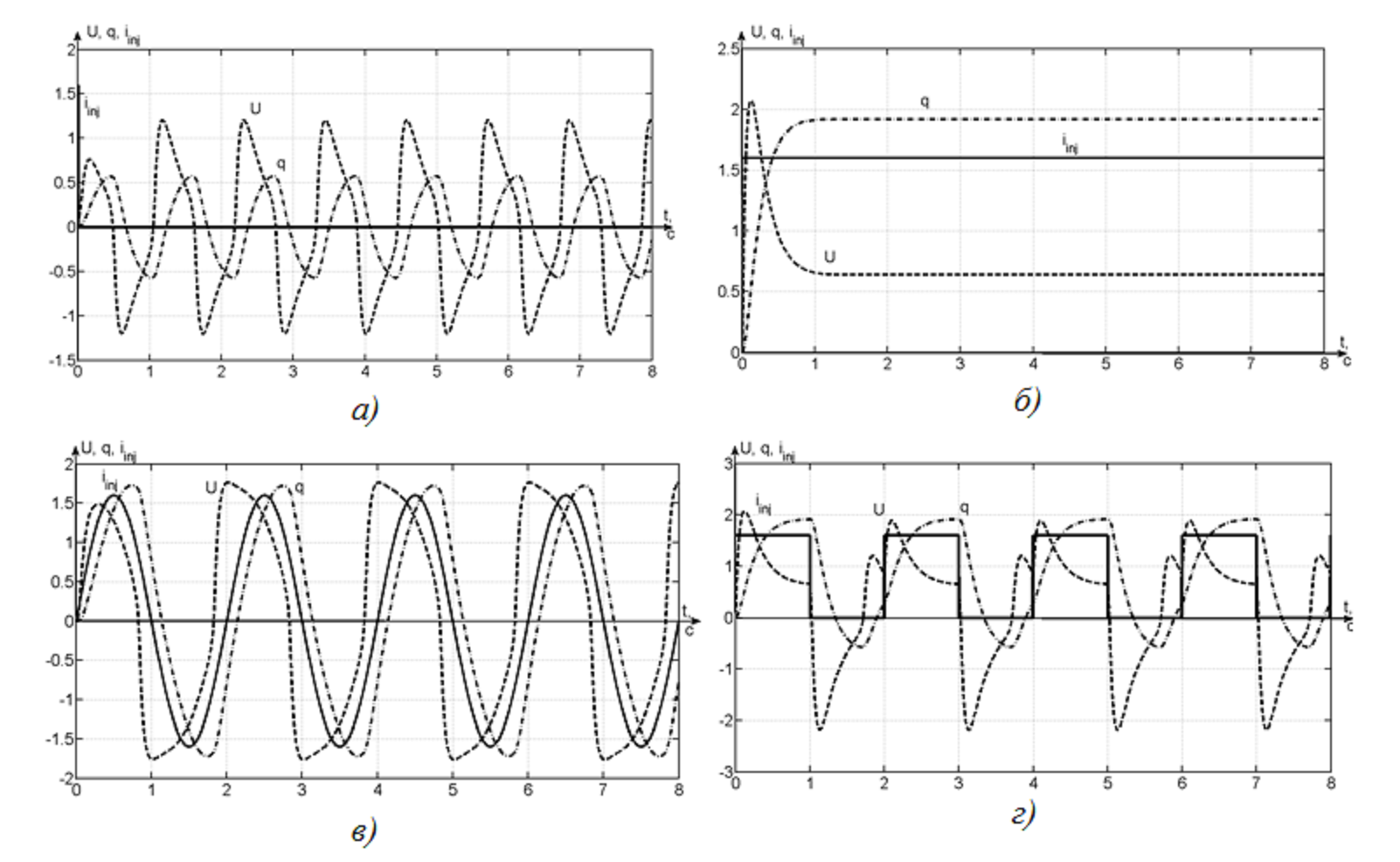
Рисунок 4 – Реакція осцилятора на різні вхідні впливи:
а) імпульс; б) стрибок; в) синусоїду (T = 0,5 с); г) меандр (T = 0,5 с)
В результаті моделювання отримані коливання різного характеру: а) релаксаційного ангармонічного з частотою 1,11 Гц; б) аперіодичного при постійній часу 0,25 с; в) квазігармонічного при синусоїдальному джерелі; г) ангармонічного при прямокутних імпульсах джерела.
Наведені коливання характеризують основні режими роботи осцилятора Ровата-Сильверстона [16], відображають його властивості генерувати як аперіодичні сигнали, так і періодичні. В даному випадку синхронізація з періодичним вхідним впливом (синусоїда, меандр) є не типовою для біологічних систем, де «запалюванням» нейрона керували дискретні імпульси струму (як у випадку рис. 4.а).
Розглянута проста модель штучного осцилятора не враховує окремі властивості свого біологічного двійника – нейрона центрального генератора рухів. Наприклад, вона не бере до уваги тимчасові затримки, які впливають на динаміку системи. І, що більш важливо, окремий осцилятор не враховує впливів синхронізуючої функції біологічного нейрона, яку ряд дослідників вважають вирішальною. Останнє явище часто застосовується для генерації ритмічних рухів антропоморфних роботів, так як моделює природну для людини процедуру взаємодії з навколишнім середовищем (жестикуляція, періодично повторювані дії і тощо). Однак, ряд робіт свідчить, що властивістю автосинхронізаціі володіє пов'язана пара осциляторів Ровата-Сильверстона, що і є найбільш типовим випадком в біологічних системах. Це буде предметом наших майбутніх досліджень.
Висновки
Дана магістерська робота виконується для удосконалення та перевірки надійності системи управління піддатливістю електромеханічних роботів зі складною кінематикою. Передбачається застосування біологічно подібних контролерів (нелінійних осциляторів), що дозволить підвищити адаптивність системи по відношенню до варіації її параметрів і умов роботи, що особливо важливо для випадку взаємодії робота з людиною.
В рефераті приводиться моделювання біологічно-подібного осцилятора Ровата-Сильверстон, вивчення якого продовжиться надалі.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Перелік посилань
- Taghirad H.D., Bélanger P.R. Modeling and parameter identification of Harmonic Drive systems // Journal of Dynamic Systems, Measurements, and Control. – 22 p. [электронный ресурс]. – Режим доступа:
http://saba.kntu.ac.ir/eecd... - Tischler N. Stiffness control of robot manipulator // Proceedings 2001 ICRA IEEE International Conference on Robotics and Automation Cat No01CH37164 (2001), p. 3042 – 3046 [электронный ресурс]. – Режим доступа: http://masters.donntu.edu...
- Schaffer A. A., Hirzinger G. State feedback controller for flexible robots: A globally stable approach implemented on DLR’s light-weight robots // Robotics and Automation, 2007 IEEE International conference, 2007, p. 3824 – 3830 [электронный ресурс]. – Режим доступа: http://www.morpha.de/morpha_page...
- Luca A. D., Siciliano B., Zollo L. PD control with on-line gravity compensation for robots with elastic joints //Automatica 41(2005), 1809 – 1819.
- Ott C., Schaffer A. A., Kugi A. – A passivity based cartesian impedance controller for flexible joint robots – Part 1: Torque feedback and gravity compensation [электронный ресурс]. – Режим доступа: https://www.google.com...
- Liu G.P., Daley S. Optimal-tuning PID control for industrial systems // Control Engineering Practice 9 (2001)
p. 1185 - 1194 [электронный ресурс]. – Режим доступа: http://www.sciencedirect.com... - Bruno S., Oussama K. – Handbook of Robotics, 2008, LX, p. 7 – 9 [электронный ресурс]. – Режим доступа: http://books.google.com.ua/books...
- Serhan H., Nasr C. G., Henaff P. – Muscle emulation with DC motor and neural networks for biped robots // Int J Neural Syst. 2010 Aug; 20(4): 341 – 53.
- Rowat P.F., Selverston A.I. Oscillatory mechanisms in pairs of neurons connected with fast inhibitory synapses // Journal of Computational Neuroscience 4. – Kluwer Academic Publishers, 1997. – 25 p. [электронный ресурс]. – Режим доступа: http://crayfish.ucsd...
- Кузнецов А.П., Кузнецов С.П., Рыскин Н.М. Нелинейные колебания. Учеб. пособие для вузов. – М.: Издательство физико-математической литературы, 2002. – 292 с. [электронный ресурс]. – Режим доступа: http://www.sgtnd.narod.ru...
- Кириллов С.Ю., Клиньшов В.В. Исследование динамических режимов модели нейрона с последеполяризацией // Труды научной конференции по радиофизике. – ННГУ, 2007. – 86 с. [электронный ресурс]. – Режим доступа: https://www.google.com/url...
- Мельник А.А., Хоменко В.Н., Плис П.С., П. Энафф, Борисенко В. Ф. – Кинематическая модель робота с шестью степенями свободы и возможностью учета зазора в суставах. Научные труды ДонНТУ, 10(180) 2011, 113 – 120 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal...
- Рябченко В.В., Дацун Н.Н. Программно-аппаратный комплекс управления роботами-манипуляторами фирмы Neuronics AG // Материалы 4-й международной научно-технической конференции "Моделирование и компьютерная графика – 2011". Донецк, 5-8 октября 2011 г. С. 295 – 299 [электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080...
- Рябченко В.В., Дацун Н.Н. Использование моделирующей среды для создания программного обеспечения программно-аппаратного комплекса управления роботом-манипулятором семейства Katana фирмы Neuronics AG // Наукові праці Донецького національного технічного університету 14 (188), 2011. – 335 – 339 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal...
- Snegina E., Pougatch A., Khomenko V., Melnyk A., Henaff P., Borysenko V. Practical aspects of Rowat-Selverston
bio-inspired oscillator simulation // Наукові праці Донецького національного технічного університету 11 (186), 2011. – 369 – 373 [электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal... - Amrollah E., Henaff P. On the role of sensory feedbacks in Rowat–Selverston CPG to improve robot legged locomotion // Frontiers in Neurosciences. Neurorobotics 4, 113, 2010. – 9 p. [электронный ресурс]. – Режим доступа: http://www.ncbi.nlm.nih.gov...
