Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы и постановка задач
- 2. Обзор исследований и разработок по теме
- 3. Моделирование инструмента
- 4. Определение элементарных составляющих силы резания
- 5. Анализ напряженно-деформированного состояния конструкции сборного сверла
- Выводы
- Список источников
Введение
С каждым годом все более жесткими становятся требования к конструкционным материалам, из которых изготавливаются ответственные детали и узлы, тяжело нагруженные элементы. Одним из путей улучшения свойств металлов является их легирование и соответствующая термическая обработка. В результате получают заданные эксплуатационные характеристики деталей, но это приводит к усложнению их обработки. Например, железнодорожные рельсы подвергают объемной закалке, вследствие чего обработка отверстий в рельсах под крепежные элементы возможна лишь твердосплавным инструментом.
1. Актуальность темы и постановка задач
В настоящее время для лезвийной обработки отверстий в рельсах применяют сборные сверла с механическим креплением сменных неперетачиваемых пластин (СНП). На практике установлена относительно невысокая стойкость данного инструмента. Основной причиной потери работоспособности является выкрашивание режущих кромок и сколы вершин. Характерные виды износа сменных неперетачиваемых пластин приведены на рисунке 1.

Рисунок 1. Характерный вид износа сменных неперетачиваемых пластин
Периферийная и центральная пластины работают в разных условиях, поэтому характер износа в них отличается. Для периферийной пластины характерной чертой является износ по задней поверхности и скалывание вершины пластины, которая находится на максимальном диаметре (рис. 1). Для центральной пластины, расположенной вблизи оси сверла, характерным является выкрашивание участка режущей кромки, который расположена ближе к оси сверла (рис. 1).
Причинами низкой работоспособности сборных твердосплавных сверл считаются тяжелые условия резания, вызванные особенностями процесса сверления – скоростью резания возле оси инструмента равной нулю, и изменяющейся геометрией и как следствие - переменными составляющими силы резания вдоль режущих кромок центральной и периферийной пластин. Одним из путей повышения работоспособности сборных сверл является создание инструмента с рациональными конструктивными и геометрическими параметрами, которые обеспечивают более равномерную загрузку режущих кромок и минимизацию неуравновешенной радиальной составляющей силы резания, которая возникает во время сверления.
2. Обзор исследований и разработок по теме
В [2] описана методика определения амплитуды колебания при обработке металлов резанием. Процесс резания часто сопровождается колебаниями со сравнительно небольшой амплитудой, известными под названием вибрации. Колебания, с одной стороны, отрицательно сказываются на работе станка, точности и качестве обрабатываемого изделия, с другой стороны, могут оказывать положительное влияние, например при вибрационной обработке.
В связи с этим основными задачами динамики процесса резания являются:
- Изучение причин возникновения и развития колебаний;
- Изучение устойчивости системы СПИД и изыскание эффективных методов устранения колебаний;
- Определение рациональных режимов вибрационной обработки.
На металлорежущих станках встречаются различные виды колебательных движений. Наряду с собственными колебаниями, в процессе резания возможны вынужденные колебания, возникающие при работе многолезвийного инструмента, обработке изделий с неравномерным припуском и другие, а также автоколебания в само возбуждающихся системах. Собственные колебания происходят в системе при изменении ее состояния, определяющего необходимую энергию для возбуждения этих колебаний. Вынужденные колебания возникают под действием периодической силы, источник которой дает энергию колебаний. Автоколебания возбуждаются в отсутствие внешнего периодического воздействия и определяются устройством самой системы, при этом источник энергии является неотделимой частью системы.
Трудность изучения колебательного движения заключается не только в его многообразии и сложности, но и в том, что процессу резания присущ целый ряд нелинейных зависимостей, например, нелинейная зависимость силы резания от толщины срезаемого слоя, нелинейная зависимость силы резания от скорости. Для анализа колебательного движения при резании металлов необходимо составить математическую модель системы. Выбор схемы этой модели, прежде всего, связан с определением числа степеней свободы, т. е. числа независимых переменных, необходимых для полного описания процессов в системе СПИД. Реальная система металлорежущего станка обычно имеет большое число степеней свободы, каждой из которых отвечает своя собственная парциальная частота. При составлении математической модели можно пренебречь некоторыми степенями свободы, если эти степени связаны с частотами, значительно отличающимися по величине от основных (лимитирующих) частот системы. Поэтому каждому исследованию колебательных движений должно предшествовать определение собственных парциальных частот. Если нет возможности аналитического решения этой задачи, производится экспериментальное определение парциальных частот по осциллограммам затухающих колебаний.
После измерения частот и определения числа степеней свободы устанавливаются другие параметры колебательных контуров математической модели:
- По осциллограммам затухающих колебаний вычисляется логарифмический декремент;
- На основании диаграммы нагрузка-перемещение определяется жесткость системы;
- С учетом жесткости и собственной частоты вычисляется величина приведенной массы;
- Устанавливается характеристика силы резания и при необходимости характеристика силы трения;
- При наличии внешней возмущающей силы определяется ее амплитуда и частота.
Окончательное суждение о правильности принятой модели и значений ее параметров дает сравнение результатов математического анализа с экспериментальными данными.
Для описания вынужденных колебаний системы станка составляются дифференциальные уравнения. Методика написания дифференциальных уравнений вынужденных колебаний систем станков рассмотрена в [2]:
В процессе резания появление внешней периодической силы может быть обусловлено следующими причинами:
- Работой многолезвийного инструмента;
- Наличием неравномерного припуска;
- Возможностью образования элементной стружки.
Последнее более значимо в области малых значений скорости резания, когда частота образования элементов сопоставима с собственной частотой системы. Кроме того, вынужденные колебания могут возникнуть в системе СПИД от привода станка, несбалансированных вращающихся масс и т. д. Влияние условий обработки на статическую и динамическую компоненты силы резания рассмотрены в [3, стр.314-332]: Процесс фрезерования характеризуется прерывистостью резания и мгновенно изменяющейся толщиной среза, что приводит к возникновению колебаний силы резания, которые в свою очередь вызывают нежелательные вибрации в технологической системе, высокую шероховатость обработанной поверхности и поломку инструмента.
Вместе с тем, неоднозначны литературные данные о составе спектра силы резания при фрезеровании концевыми фрезами, а именно: в одних источниках утверждается, что динамическая составляющая силы резания изменяется на частоте fz прохождения зубьев через зону резания, а в других, что колебания силы резания происходят на частоте вращения фрезы f0 и частоте fz.
В связи с этим возникает необходимость исследования характера изменения силы резания при фрезеровании плоскости концевой фрезой и установления доминирующей частоты ее изменения. Кроме этого известна математическая модель главной составляющей силы резания при фрезеровании концевыми фрезами, однако эмпирическая модель динамической составляющей силы резания отсутствует. Проведенные исследования показали, что из-за влияния радиального биения фрезы спектр силы резания сдвигается от частоты fz прохождения зубьев через зону резания к частоте вращения шпинделя. Это может оказывать вредное влияние на процесс резания, поскольку доминирующими в спектре силы резания становятся более низкочастотные гармоники.
Кроме того, установлено, что при наличии биения фрезы разница в мощности гармоник на оборотной и зубцовой частотах находится в обратно пропорциональной зависимости от величины минутной подачи. С уменьшением подачи влияние биения концевой фрезы на сдвиг частот проявляется заметнее. Следовательно, при наличии эксцентриситета низкочастотные составляющие силы резания будут оказывать еще большее влияние на качество окончательной обработки.
Зная частотный состав спектра силы резания и характер ее изменения при фрезеровании плоскостей концевой фрезой, можно перейти к установлению закона изменения динамической составляющей силы резания. В [3] приведена методика разработки эмпирическая модель динамической составляющей силы резания.
3. Моделирование инструмента
На этапе проектирования режущего инструмента возможно спрогнозировать каким образом будут влиять конструктивные и геометрические параметры на напряженно-деформированное состояние рабочей части сборного сверла с помощью численного моделирования и прикладных программ на их основе. С целью анализа влияния конструктивных и геометрических параметров рабочей части сборного сверла на ее напряженно-деформированное состояние, нами была создана трехмерная геометрическая модель (рис. 2) и проведена ее дискретизация (рис. 3).
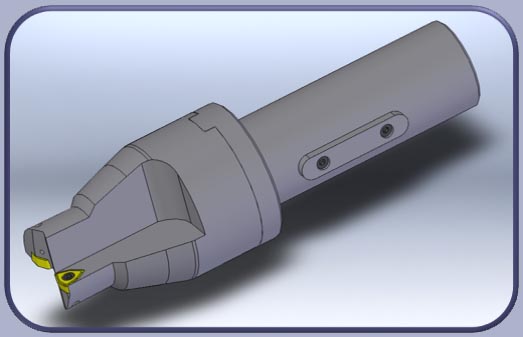
Рисунок 2. Модель сборного сверла
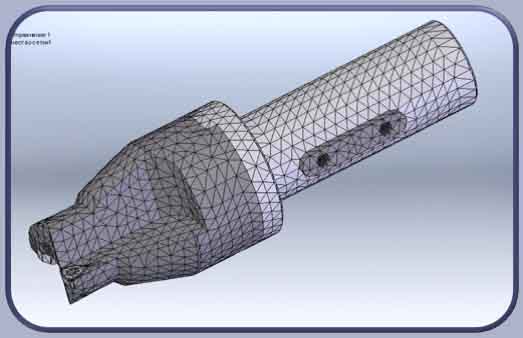
Рисунок 3. Дискретизация модели
Моделирование проводилось для условий обработки сверлом со стандартными конструктивными и геометрическими параметрами на центральной и периферийной пластинах. Начальные условия расчета соответствовали статическому анализу сборной конструкции с учетом коэффициента трения между элементами сверла и их относительной кинематики.
Кинематические граничные условия имитировали закрепление хвостовика сверла в оправке (рис. 4), а нагрузка соответствовала силам закрепления элементов сверла и распределению составляющих силы резания вдоль режущих кромок пластин в соответствии с геометрией (рис. 5).
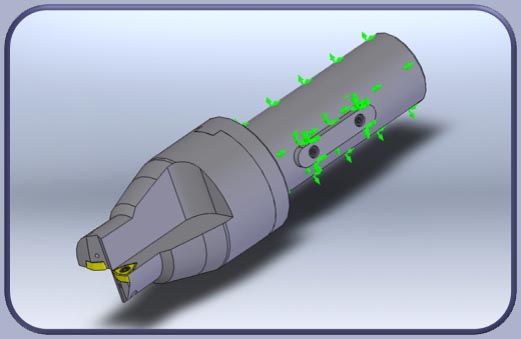
Рисунок 4. Кинематические граничные условия модели
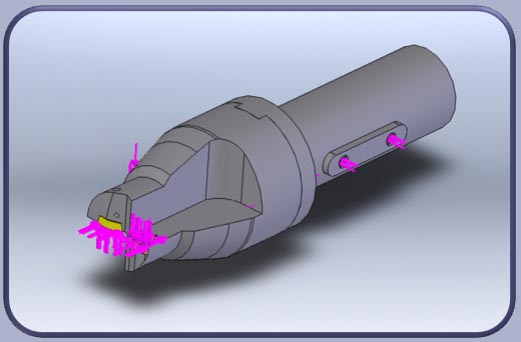
Рисунок 5. Нагрузка модели
Для этого были проанализированы геометрические параметры сверла вдоль режущих кромок и нагрузки, возникающие на режущих кромках каждой сменной неперетачиваемой пластины в процессе резания.
4. Определение элементарных составляющих силы резания
На основе имеющейся расчётной схемы (рис. 6) и аналитических исследований [1] определены элементарные составляющие силы резания, действующие в отдельных точках режущих кромок концевых инструментов, которые имеют следующий вид:
- элементарная тангенциальная составляющая:
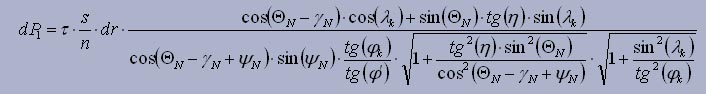
- элементарная осевая составляющая:
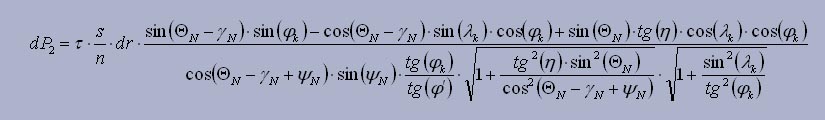
- элементарная радиальная составляющая:
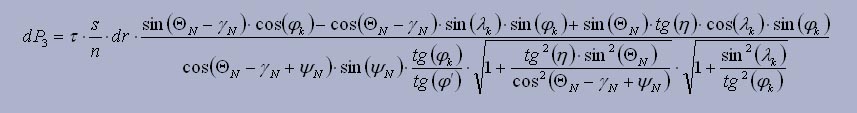
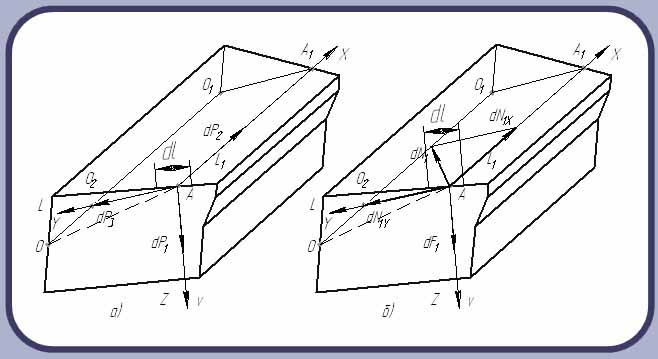
Рисунок 6. Схема сил, действующих на передней (а) и задней (б) поверхностях зуба сверла
В результате были получены эпюры распределения составляющих силы резания, действующих вдоль главной режущей кромки периферийной (рис. 7) и центральной (рис. 8) пластин.
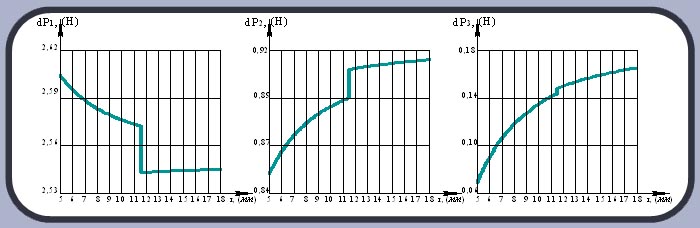
Рисунок 7. Эпюры распределения составляющих силы резания, действующих вдоль главной режущей кромки периферийной пластины
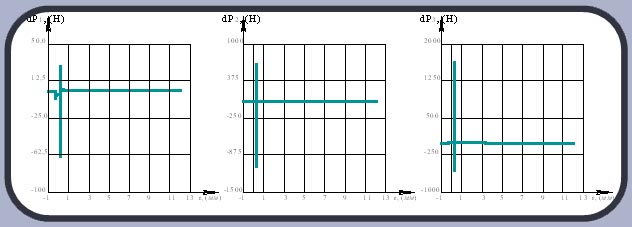
Рисунок 8. Эпюры распределения составляющих силы резания, действующих вдоль главной режущей кромки центральной пластины
5. Анализ напряженно-деформированного состояния конструкции сборного сверла
В результате расчета была получена информация о напряженно-деформированном состояние конструкции сборного сверла. На рисунке 9 приведены деформации конструкции и ее элементов. Для большей наглядности приведена деформированная форма инструмента с увеличением деформаций в 100 раз.
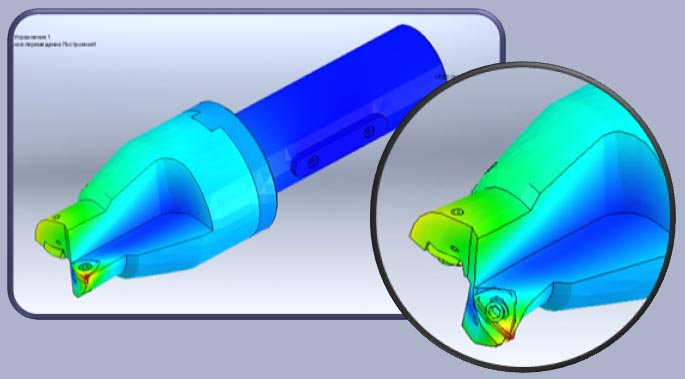
Рисунок 9. Напряженно-деформированное состояние конструкции сборного сверла
На рисунке 10 приведенны эквивалентные напряжения, рассчитанные по критерию Мизеса.
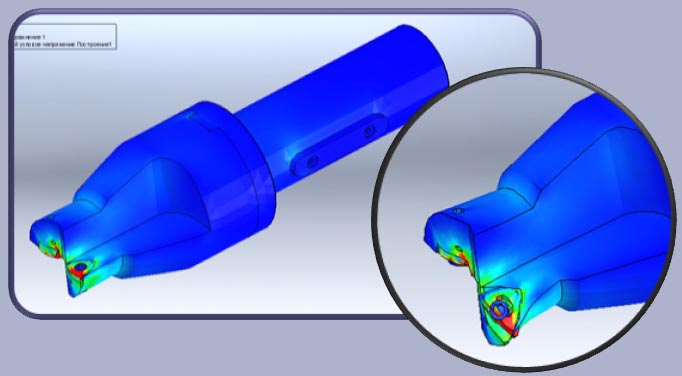
Рисунок 10. Эквивалентные напряжения, рассчитанные по критерию Мизеса
Выводы
Проведенное моделирование показало, что расчетное распределение перемещений и напряжений в конструкции сборного сверла соответствует действительному распределению нагрузки. Это подтверждается тем, что места с максимальными значениями перемещений и напряжений на модели (рис. 9) соответствуют местам разрушения режущих пластин на реальной конструкции сверла (рис. 1). Таким образом, делаем вывод о возможности применения численного моделирования при поиске рациональной конструкции сборного сверла, которая обеспечит относительно равномерную загрузку режущих кромок инструмента и повышения его работоспособности.
В дальнейшем планируется провести экспериментальное исследование с целью подтверждения выдвинутых гипотез, с учётом изменения геометрических параметров рабочей части сверла, силовых и динамических параметров процесса.
Примечание:
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2012 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Холмогорцев Ю. П. Оптимизация процессов обработки отверстий / Холмогорцев Ю. П. – М.: Машиностроение, 1984. – 184 с.
- Мурашкин Л. С., Мурашкин С. Л. Прикладная нелинейная механика станков /«Машиностроение», 1977. – 192с.
- Васин С. А., Маслов А. Р. Прогнозирование виброустойчивости инструмента при точении и фрезеровании / М.: Машиностроение, 2006. – 384с.
- Денисенко В. И. Управление стружкоотводом при сверлении / В. И. Денисенко// Известия высших учебных заведений. Машиностроение. – 1988. – Вып. 7. – С. 141 – 145.
- Виноградов А. А. Расчёт усадки стружки и длины контакта её с резцом / А. А. Виноградов // Сверхтвёрдые материалы. – 1990. – №2. – С.58–63.
- ГОСТ 51685-2000 Рельсы железнодорожные. Общие технические условия. – М.: Издательство стандартов, 2001. – 27 с.
- Баканов А.А., Петрушин С.И. Работоспособность сверл с СМП при сверлении железнодорожных рельсов // Современные проблемы машиностроения: Труды III Междунар. научнотехн. конф. – Томск: Изд_во ТПУ, 2006. – С. 186–189.
- Петpушин С.И., Баканов А.А., Махов А.В., Геометрический и силовой анализ сбоpных свеpл со сменными многогpанными пластинами/Технология машиностроения, Вып. 10(64), 2007. – С. 27 – 30.
- Справочник технолога машиностроителя: в 2 т. /[ред.: Косилова А. Г., Мещеряков Р.К.]. - 4-е изд., перераб. и доп. - М.:Машиностроение, 1986. Т.2 - 1985. – 496 с.
- Гринёв Ю.А. Определение статических геометрических параметров сборных сверл / Ю.А. Гринёв, Т.А. Воеводина, Е.Н. Царенко // Наукові праці Донецького національного технічного університету. Серія: Машинобудування і машинознавство. Донецьк: ДонНТУ, 2011. – Випуск 8 (190). – С. 200 – 209
