Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Анализ существующих конструкций шлаковоза
- 2.1 Шлаковоз с винтовым механизмом кантования чаши
- 2.2 Зубчатый механизм кантования чаши шлаковоза
- 3. Описание предлагаемой конструкции четырехзвенного механизма кантования чаши шлаковоза
- 4 Расчетная часть
- 4.1 Синтез и кинематическое исследование четырехзвенного механизма
- 4.2 Определение координат центра тяжести и объема жидкости, моделирующей шлак
- 4.3 Расчет момента сопротивления кантованию чаши
- Выводы
- Перечень ссылок
Введение
Кислородно-конвертерное производство стали в настоящее время является одним из лидирующих, поскольку оно позволяет в короткие сроки переплавлять передельный чугун в высококачественную сталь. Процесс выплавки стали сопровождается выходом побочных продуктов, одним из которых является шлак. На многих крупных металлургических предприятиях утилизация шлака достигает 70÷80% и более. В настоящее время поставлена и решается задача переработки всего металлургического шлака в годный для строительной индустрии продукт и полной ликвидации на территории заводов шлаковых отвалов. Основное количество шлака гранулируют, некоторую часть перерабатывают на щебень, пемзу, шлаколитые изделия, минеральную вату, минеральные удобрения. Грануляцию осуществляют на некотором удалении от печи или цеха [1].
Для уборки шлака от печей и транспортировки его на переработку или в отвал применяют шлаковозы. К шлаковозам предъявляют следующие основные требования: форма чаши должна способствовать беспрепятственному выходу из нее затвердевшего шлака на шлаковом отвале; должна быть исключена возможность самопроизвольного опрокидывания чаши как при его кантовании, так и при движущемся или остановленном шлаковозе; должна быть обеспечена поперечная устойчивость шлаковоза при опрокидывании чаши как груженой, так и порожней; конструкция, форма и материал чаши, а также способ ее крепления должны обеспечивать высокую долговечность чаши; привод механизма кантования должен допускать возможность регулировки скорости слива шлака на грануляционных установках [1].
Поэтому был специально разработан и исследован с помощью современных технических средств – кривошипно-шатунный механизм кантования чаши шлаковоза. Так же был исследован сам процесс кантования чаши, а именно, характер изменения момента сопротивления при кантовании чаши.
1. Актуальность темы
Металлургические предприятия относятся к числу наиболее крупных народнохозяйственных объектов, в значительной степени определяющих уровень экономического развития. Из всего многообразия техногенных образований, получаемых в металлургическом производстве, основной объем (до 80%) от общего количества твердых промышленных отходов (ТПО) составляют шлаковые отвалы. Переработка шлаков определяет практическую сущность организации безотходного металлургического производства
Расположенные в городской черте шлаковые отвалы нарушают ландшафт территорий, для размещения отвалов отчуждаются земельные угодья, ухудшается экологическая обстановка региона.
В настоящее время в большинстве высокоразвитых стран использование силикатной продукции металлургических предприятий достигает 90%. В строительной индустрии используются их вяжущие свойства. Однако самое ценное, что находится в шлаке это металл. Способов извлечения металла из жидких шлаков, опробованных в промышленных условиях, нет. Поэтому металл на предприятиях извлекается только из твердых шлаков при первичной переработке на гранулированной установке и при вторичной — на дробильно-сортировочных установках.
Существующие в данный момент времени механизмы опрокидывания чаши шлаковоза, не могут обеспечить равномерное сливание шлака на гранулированные установки для получения гранул из шлака одинаковой фракции для удобства переработки на дробильных установках
Столкнувшись с этим вопросом, был найден ответ при исследовании и конструировании физической модели кривошипо-шатунного механизма кантования, который обеспечивает равномерное сливание шлака на гранулированные установки, что обеспечивает более эффективную переработку шлака с меньшими затратами.
2. Анализ существующих конструкций шлаковоза
В настоящее время, на предприятиях металлургического комплекса, эксплуатируют шлаковозы отличающиеся не только объемом чаш, но и конструкцией механизмов их кантования.
2.1 Шлаковоз с винтовым механизмом кантования чаши
Винтовой механизм кантования чаши (рис. 2.1), смонтированный на раме, включает в себя: электродвигатель 14 переменного тока; одноступенчатый цилиндрический редуктор 13; промежуточный вал, соединенный с редуктором муфтой и несущий на себе шестерню 12; пару находящихся в зацеплении друг с другом одинаковых цилиндрических зубчатых колес 11, одно из которых получает вращение от шестерни 12; два параллельно расположенных, смонтированных на подшипниках качения грузовых винта 10 с трапецеидальной самотормозящей резьбой; две гайки 9, закрепленные в траверсе 8, которая свободно закреплена (на втулке) на одной из цапф 6 опорного кольца. Шестерня 12 и колеса 11 закрыты кожухом.
Через систему передач вращение от электродвигателя 14 преобразовывается винтами 10 в поступательное движение гаек 9 и траверсы 8, а следовательно и опорного кольца с чашей. Находясь в зацеплении с неподвижными рейками 3, зубчатые секторы 5 при этом обкатываются по ним, приводя во вращение опорное кольцо с чашей.
Таким образом, при движении катков 7 по направляющим 4 происходит опрокидывание чаши при одновременном перемещении ее от середины рамы шлаковоза к краю. По мере приближения чаши к краю рамы, угол поворота чаши возрастает достигая 116÷118 град за 1,3÷1,5с. Опрокидывание можно производить в обе стороны. Выключение электродвигателя при достиженижении чашей крайних положений осуществляется командоаппаратом 1, связанным с нижним винтом 10 посредством кинематичной червячной передачи 2. Рассмотренный механизм имеет малый срок службы винтов и гаек в связи с тяжелыми условиями их работы [2].
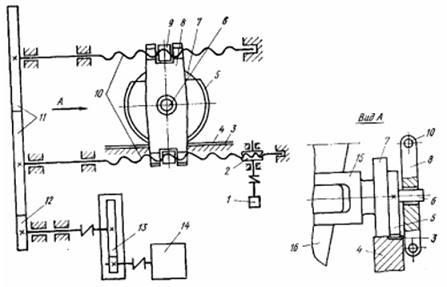
Рисунок 2.1 – Кинематическая схема винтового механизма кантования чаши шлаковоза
2.2 Зубчатый механизм кантования чаши шлаковоза
В данном типе конструкции шлаковоза кантование чаши происходит через зубчатые передачи (рис. 2.2.). От фланцевого электродвигателя 1 через самотормозящийся редуктор 2 с консольной шестерней 10 вращение передают зубчатому сектору 3, который четко закреплен на цапфе 7 опорного кольца 4 чаши. Сектор 3 и опорное кольцо вместе с другим зубчатым сектором 5, выполненным вместе с катком 6, перемещают путем обкатывания сектором 5 и катком 6 неподвижных зубчатых и гладких сегментов 11, которые установлены на стойках лафета 13. При этом обеспечивают перемещение опорного кольца с чашей в направлении, перпендикулярном оси железнодорожного пути и поворота чаши на угол до 118°.
Постоянство межцентрового расстояния между осью выходного вала редуктора 2 и осью цапф 7 опорного кольца 4 при кантовании обеспечивается водилами 12, которые закреплены на цапфах 7 опорного кольца 4 и соединены с осями 14 лафета 13 [2].
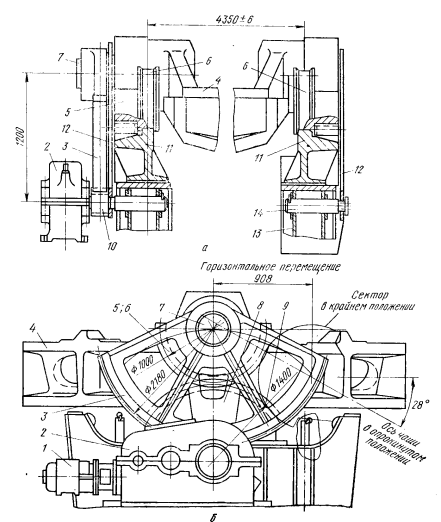
Рисунок 2.2 – Зубчатый механизм кантования чаши шлаковоза
3. Описание предлагаемой конструкции четырехзвенного механизма кантования чаши шлаковоза
Кинематическая схема четырехзвенного механизма кантования чаши шлаковоза приведена на рисунке 3.1. От мотор-редуктора 1 передается крутящий момент на кривошип 2, который жестко закреплен на выходном валу мотор-редуктора. Кривошип 2 через шатун 3 передает усилие на рычаг 4, который жестко закреплен на цапфе чаши шлаковоза. В следствии поворота рычага 4 происходит кантование чаши, при этом чаша перемещается на некоторое расстояние перпендикулярно железнодорожным путям. При кантовании чаши зубчатое колесо 5 и ролик 6, которые жестко закреплены на цапфе чаши, перемещаются соответственно по рейке 7 и дорожке 8, которые установлены на раме шлаковоза. Следует отметить, что при полном обороте кривошипа 2 происходит полный цикл кантования чаши, а именно как кантование, так и возвращение чаши в исходное положение.
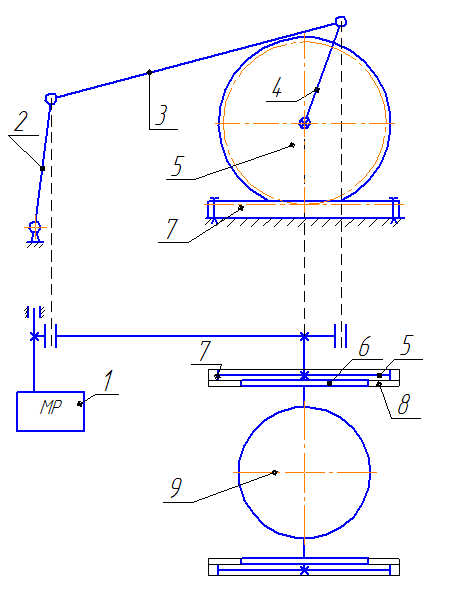
Рисунок 3.1 - Кинематическая схема четырехзвенного механизма кантования чаши шлаковоза
4 РАСЧЕТНАЯ ЧАСТЬ
4.1 Синтез и кинематическое исследование четырехзвенного механизма
Целью синтеза четырехзвенного механизма является определение геометрических размеров звеньев и координат центра оси вращения кривошипа. Данную задачу можно решить графическим путем с использованием программы «Компас 10» (рис. 4.1). Для этого, предварительно сняв необходимые геометрические замеры с модели шлаковозной тележки, рисуем в «Компасе 10» упрощенный вид тележки. Далее задаемся, исходя из конструктивных соображений, длиной: кривошипа l1 , шатуна l2 и рычага l3 , а так же учитываем что центр цапфы чаши, при вертикальном расположении чаши φ=0°, расположен на одной оси с выходным валом редуктора , на котором жестко закреплен кривошип. Поскольку центр оси цапфы во время кантования претерпевает горизонтальное перемещение, а рычаг жестко закреплен на цапфе опорного кольца чаши, то получаем что при повороте чаши на определенный угол – рычаг тоже будет поворачиваться на этот угол. Зная, что начальный угол поворота φ0=0°, а конечный φк=120° – разбиваем механизм поворота на четыре положения при перемещении угла поворота чаши на 30°.
Полученные размеры: l1 =1000мм, l2 =2200мм, l3 =1370мм.
Кинематический анализ механизма включает в себя определение скоростей и ускорений точек звеньев, угловых скоростей поворота чаши и вращения кривошипа, построение графиков их зависимости от угла поворота чаши и планов скоростей и ускорений.
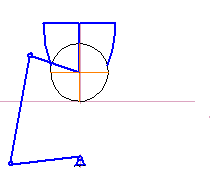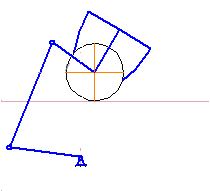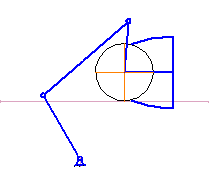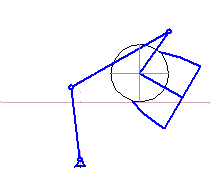
Рисунок 4.1 – Синтез рычажного механизма
(анимация: объём 7,3 кб, кадров 5, количество циклов повторений 8, задержка между кадрами 1 с)
При угле поворота чаши φ1=0° (рис.4.2).
Угловую скорость поворота чаши можно определить по формуле:
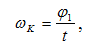
где φ1 – угол поворота чаши;
t – время за которое чаша поворачивается на этот угол.
Рисунок 4.2 – Положение механизма при φ = 30°
При угле поворота чаши φ1=30° время этого поворота равно:
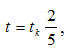
где tк – время кантования чаши, задаемся tк=75с.
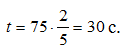
Тогда угловая скорость при данном угле поворота равна [5]:
Скорость т. В можно разложить на переносную вместе с центром оси цапфы и относительную, вызванную вращением относительно МСЦ. Векторная формула будет иметь следующий вид [5]:
Очевидно, что вектор относительной скорости т.В будет направлен перпендикулярно СВ, а вектор переносной скорости – параллельно перемещению оси цапфы. Значение этих скоростей можно определить по формулам:
R – радиус зубчатого колеса, R=0,62м;
l1 – длина рычага, l1=1м,
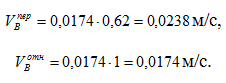
Строим план скоростей для данного положения рычагов (рис.4.3). Принимаем масштабный коэффициент μ=2·10-3 (м/с)/мм . Векторы переносной и относительной скоростей т.В будут исходить из полюса Рv согласно своим направлениям имеют длину [5]:
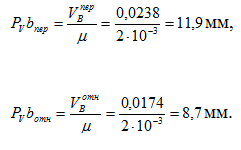
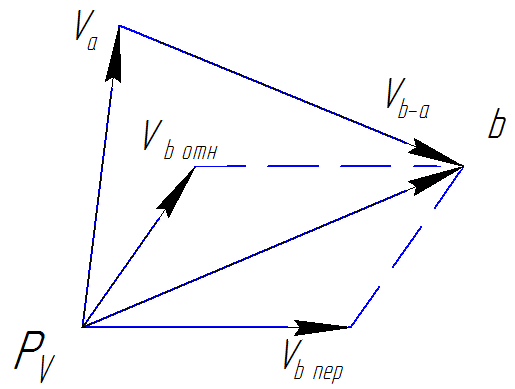
Рисунок 4.3 – План скоростей для положения φ=30° (μ=2·10-3(м/с)/мм)
Строим вектор скорости т. В сложив векторы ее переносной и относительной скоростей. Измерив его длину определяем значение скорости т.В:
Для определения скорости т.А составим другое векторное уравнение [5]:
где  – вектор скорости т. А, направленный перпендикулярно ОА;
– вектор скорости т. А, направленный перпендикулярно ОА;
 – вектор скорости т.В относительно т.А, который направлен перпендикулярно ВА.
– вектор скорости т.В относительно т.А, который направлен перпендикулярно ВА.
Проводим из полюса прямую, перпендикулярную ОА, а из конца вектора  прямую перпендикулярную ВА, и в месте их пересечения будет конец вектора скорости
прямую перпендикулярную ВА, и в месте их пересечения будет конец вектора скорости  и начало вектора скорости
и начало вектора скорости  . Замерив длины этих векторов можем определить их значения:
. Замерив длины этих векторов можем определить их значения:
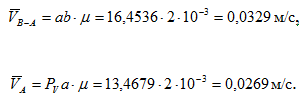
Угловую скорость кривошипа определим по формуле [5]:
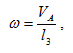
где l3=1,37 м.
Ускорение т.А векторно можно разложить [5] на нормальное и тангенциальное:
Поскольку угловая скорость кривошипа постоянна ω=const, то тангенциальное ускорение т.А:
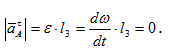
Следовательно:
Строим план ускорений для данного положения рычагов (рис. 4.4). Принимаем масштабный коэффициент  . Вектор ускорения т. А будет исходить из полюса Pa и направлен параллельно ОА от А к О. Его величину определим по формуле:
. Вектор ускорения т. А будет исходить из полюса Pa и направлен параллельно ОА от А к О. Его величину определим по формуле:
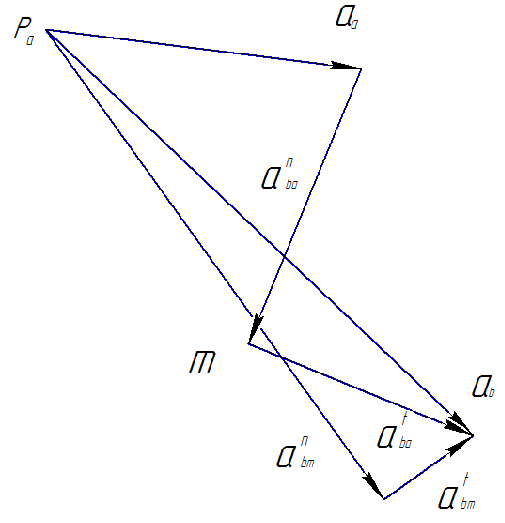
Рисунок 4.4 – План ускорений для положения φ=30° (μ=2·10-5(м/с2)/мм)
Вектор ускорения т.В, как принадлежащей шатуну, можно представить в виде векторной суммы [5]:
где  – вектор ускорения т.В относительно т.А нормальное, которое направленно параллельно ВА от В к А;
– вектор ускорения т.В относительно т.А нормальное, которое направленно параллельно ВА от В к А;
 – вектор ускорения т.В относительно т.А тангенциальное, которое направленно перпендикулярно ВА.
– вектор ускорения т.В относительно т.А тангенциальное, которое направленно перпендикулярно ВА.
Нормальное ускорение т.В относительно т.А равно:
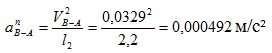
Строим вектор нормального ускорения т.В относительно т.А на плане ускорений. Он исходит из конца вектора  и равен:
и равен:
Кроме того, вектор ускорения т.В, как принадлежащей рычагу, можно разложить на следующую сумму векторов:
где  – вектор нормального ускорения т.В относительно МСЦ, направлен параллельно ВМ от В к М;
– вектор нормального ускорения т.В относительно МСЦ, направлен параллельно ВМ от В к М;
 – вектор тангенциального ускорения т.В относительно МСЦ, направлен перпендикулярно ВМ.
– вектор тангенциального ускорения т.В относительно МСЦ, направлен перпендикулярно ВМ.
Нормальное ускорение т.В относительно МСЦ определим по формуле:
где lBM – расстояние от т.В до МСЦ, lBM=1,40003 м.
Строим вектор нормального ускорения т.В относительно МСЦ на плане ускорений. Он исходит из полюса и равен:
Проводим из конца вектора  прямую, перпендикулярную ВМ. В точке их пересечения будет конец вектора ускорения т.В. Измерив длины векторов
прямую, перпендикулярную ВМ. В точке их пересечения будет конец вектора ускорения т.В. Измерив длины векторов  и
и  ,можем вычислить их значения:
,можем вычислить их значения:
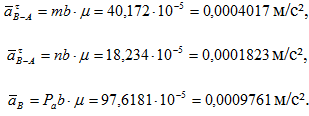
Значения угловых скоростей, скоростей и ускорений для других положений механизма вычисляются аналогично, их величины приведены в таблице 4.1.








 – координаты центра тяжести шлака,
– координаты центра тяжести шлака,  – координаты центра тяжести чаши,
– координаты центра тяжести чаши, – масса шлака,
– масса шлака, – масса чаши.
– масса чаши.



























































