Реферат
по теме выпускной работы
Содержание:
- Цель работы
- Идея работы
- Актуальность темы
- Краткий литературный обзор
- Влияние глубины резания на частоту колебаний
- Математическая модель колебательной системы
- Предварительные выводы
- Список использованной литературы
ПРИМЕЧАНИЕ: Данный автореферат составлен 14.05.2012, т.е. до окончания магистерской работы. Ориентировочная дата завершения – 15.12.2012.
Цель работы
Целью данной работы была разработка комплексной математической модели вибраций при точении, и сравнение полученных результатов с экспериментальными данными других авторов для подтверждения сделанных выводов.
Идея работы
Идеей, положенной в основу математической модели, являлось следующее предположение. В процессе точения мгновенные значения режимов резания изменяются в связи с колебаниями, что вызывает переменность силы резания. На этом основании состояние динамической системы в каждый момент времени считаем однозначно зависящим от мгновенных режимов через силу резания.
Актуальность темы работы
В последнее время в машиностроении наблюдается тенденция к высокоскоростной обработке, позволяющей сэкономить главный невосстанавливаемый ресурс - время. Основной причиной, ограничивающей режимы резания, являются вибрации, возникающие при любой обработке резанием, в том числе и при точении. Поэтому изыскание причин появления колебаний и путей борьбы с ними является приоритетными задачами современности.
При точении возникают колебания, влияющие на параметры качества и точность получаемых размеров. Математическое описание этого процесса дает возможность прогнозировать такие режимы резания, которые позволили бы избежать неблагоприятных динамических условий.
Краткий литературный обзор
Несмотря на то, что явлению вибраций в машинах посвящено весьма большое количество работ, вибрации при резании металлов и причины их появления исследованы крайне слабо.
Развитие взглядов на причину появления вибраций при точении начиналось с опытов Никольсона. Он проводил опыты по обтачиванию внешней цилиндрической поверхности на токарных станках при очень малых скоростях резания (около 1,13 мм/мин). Согласно полученным в результате данным, усилие резания благодаря образованию и последовательному скалыванию элементов стружки является переменной периодической силой, которая может вызывать ритмические колебания. На основании, этих опытов усилие резания многими авторами в течение ряда лет трактовалось как периодически изменяющаяся сила, имеющая максимум в момент наибольшей деформации элемента стружки и минимум в момент скалывания элемента [1].
Таким образом появилось представление о вибрациях при резании металлов, как о вынужденных под действием периодически изменяющегося усилия резания. Несостоятельность такого представления о вибрациях при резании металлов легко увидеть из следующего:
- Нет никаких оснований экстраполировать результаты опытов Никольсона, проведенных при чрезвычайно малых скоростях резания, на практически применяющиеся (в 20000-100000 раз большие) скорости резания. Как известно, при весьма малых скоростях, резания даже мягкие стали могут давать элементную стружку.
- Если бы изложенное объяснение природы вибраций при резании было справедливо, то, естественно, при всякой обработке металлов резанием имело бы место образование элементной стружки и появление вибраций, однако это ни в какой степени не подтверждается практикой
- Известно, что практически хрупкие металлы, например чугун и т. п., дают при обработке резко выраженную элементную стружку; в то же время такие металлы обычно не склонны к появлению вибраций, тогда как вязкие стали, дающие обычно сливную стружку, особенно часто вызывают сильные вибрации при практически применяемых скоростях резания [1].
Существует еще другое объяснение вибраций при резании металлов, а именно, что эти вибрации представляют собою резонансные колебания вследствие совпадения частот — периодических колебании усилий резания (под влиянием образования и скалывания элементов стружки) и свободных колебаний какого-либо из узлов станка.
Тейлор так формулирует это объяснение: «Когда эти периоды наибольшего и наименьшего давления синхронны или приблизительно совпадают с естественными колебаниями обрабатываемого предмета или резца, или суппорта, или какой-нибудь другой части станка, то при работе появляется дрожание».
Такое объяснение явлению вибраций дается и японским исследователем Сидзоу Дои: «При дрожании число изменений силы синхронно с числом собственных колебаний одной части токарного станка и порождает резонанс».
Согласно опытам Тейлора, причиной является совпадение частот изменений силы резания с собственной частотой колебаний какого-либо узла станка или заготовки.
После доказательства неправомерности этих точек зрения причиной вибраций стали называть механизм процесса резания, т.е. имеют место автоколебания (Манжос, Амосов, Соколовский и др.) [1, 2, 3, 4].
И.С. Амосов исследовал колебания обрабатываемой детали и инструмента в горизонтальном и вертикальном направлениях и изменение горизонтальной и вертикальной составляющих силы резания по времени. Деталь колеблется с большей амплитудой, чем инструмент; деталь и инструмент совершают колебания в двух основных направлениях с определенным сдвигом по фазе, вследствие чего их движение выражается в виде замкнутой кривой. В результате измерений колебаний и силы построена зависимость “сила-путь”. Разность полученных площадей на графике этой зависимости выражает работу, сообщенную колебательной системе [2].
Г.А. Манжос установила, что .при резании возникают автоколебания. Измерение профиля волн на обработанной поверхности показало, что волны не имеют синусоидальную форму. На основании этого был сделан вывод, что возникающие автоколебания носят резко выраженный нелинейный характер [3].
И.И. Ильницкий сделал вывод, что изменение действительного переднего угла в процессе резания возбуждает колебательные процессы, вызывая переменную силу для их поддержания. Периодическое изменение заднего угла вызывает переменную силу трения, которая поддерживает колебания в технологической системе СПИД. В отличие от других исследователей он полагал, что эта переменная сила возникает не только после образования волнистости, а немедленно в результате возмущения системы [5].
А.И. Каширин установил три причины, поддерживающие автоколебання при резании сталей: первая из них обусловлена силой трения между стружкой и передней поверхностью и между обрабатываемой деталью и задней поверхностью, вторая - переменными силами из-за изменения рабочих углов резания в процессе колебательного движения; третья, названная им вторичным возмущением, — переменным сечением среза, возникающим при движении резца по вибрационному следу от предыдущего прохода [1].
А.П. Соколовский показал, что часть силы резания ΔPy представляет собой функцию скорости относительных колебаний между инструментом и обрабатываемой деталью. Он объясняет это тем, что величина силы резания при движении резца в сторону детали отличается от силы, образующейся при движении резца в обратном направлении. Инструмент врезается в материал с меньшей силой, чем при выходе из материала, так как резец срезает материал, предварительно испытавший пластическую деформацию и поэтому упрочненный. Поэтому А.П. Соколовский принимает, что значение ΔPy зависит от отношения скорости колебаний к скорости резания [4].
Влияние глубины резания на частоту колебаний
Чтобы проанализировать влияние глубины резания на частоту колебаний при резании, рассмотрим идеализированную схему точения цилиндрической заготовки (рис. 1), совершающей колебания в радиальном направлении.
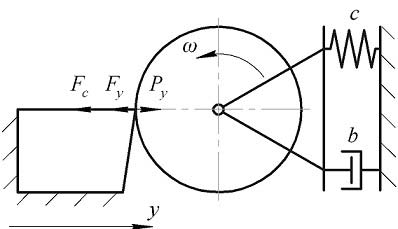
Рисунок 1 – Схема динамической системы резания с одной степенью свободы в радиальном направлении
Представим заготовку приведенной массой m, а действие жестко закрепленного резца - радиальной силой Py, обусловливающей радиальные колебания заготовки, коэффициент статической жесткости которой обозначим с. Демпфер изображает потери энергии с коэффициентом вязкого трения (диссипации) b. Радиальной силе противодействуют восстанавливающая сила Fy и сила сопротивления Fc, которые представим прямо пропорциональными перемещению и скорости колебаний соответственно:
Тогда уравнение движения будет иметь следующий вид:
Составляющую силы резания Py запишем в виде [7]:
(1) |
и представим ее зависящей от радиальных колебаний.
Чтобы рассмотреть влияние мгновенной глубины резания на частоту колебаний при обработке, будем считать глубину переменной, а все остальные величины постоянными, объединив их в коэффициент K, который, согласно (1), запишем в виде:
где Cp, Kp, n, p, x - эмпирические коэффициенты [7].
Тогда сила резания представляется так:где t - мгновенная глубина резания.
Мгновенную глубину резания можно представить суммой постоянной (номинальной глубины) и переменной частей, т.е. собственно радиальных колебаний заготовки, описываемых функцией y:
где t0 - номинальная глубина резания.
Уравнение движения примет вид:
(2) |
Пренебрежем в первом приближении потерями энергии, считая b=0 , и разложим правую часть уравнения (2) в ряд Маклорена до линейного члена. В результате получим:
(3) |
Функцию y запишем в виде:
где y1 - центрированные колебания, y2 - увод колебаний.
Определим увод колебаний из формулы (3), переписав ее в виде:
Приравняв коэффициенты при y1 и y2, получим систему двух уравнений:
 |
(4) |
Из второго уравнения системы (4) определим увод колебаний:
Из первого уравнения системы (4) найдем частоту колебаний:
 |
(5) |
Зададимся следующими исходными данными: приведенная масса заготовки m=18 кг, материал заготовки – сталь 40Х, материал режущей части инструмента – Т5К10, вылет заготовки 300 мм, диаметр заготовки 100 мм, геометрические параметры резца: α=3°, γ=9°, β=78°, φ=φ1=45°, ε=90°, λ=0°, размеры державки резца 16×25 мм, радиус скругления при вершине r=2 мм, состояние поверхности заготовки – без корки, Ra 6,3 мкм, стойкость инструмента Т=45 мин. Определим частоту вибраций заготовки по формуле (5) при различных значениях глубины резания (от 0,2 мм до 5 мм с шагом 0,2 мм) и коэффициента статической жесткости детали. Результаты вычислений сведем в таблицу 1 (с шагом глубины резания 1 мм) и построим график (рис. 2).
Глубина резания t0, мм |
Циклическая частота ω, рад/с, при коэффициенте жесткости с, Н/м: |
|||
|---|---|---|---|---|
105 |
106 |
107 |
108 |
|
1 |
200 |
298 |
761 |
2341 |
2 |
194 |
294 |
759 |
2340 |
3 |
191 |
292 |
758 |
2340 |
4 |
188 |
291 |
758 |
2340 |
5 |
186 |
289 |
757 |
2339 |
Из проведенных расчетов можно сделать вывод, что с увеличением статической жесткости заготовки влияние глубины резания на циклическую частоту радиальных колебаний заготовки уменьшается. Например, при c=105 H/м изменение частоты составляет 15%, а при c=108 - 0,1%. Из этого можно заключить, что глубина резания почти не влияет на циклическую частоту колебаний. Полученные результаты не противоречат опытным данным [1,4,5].
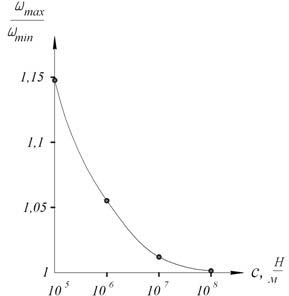
Рисунок 2 – Зависимость изменения циклической частоты от жесткости детали: ωmax – циклическая частота при t0=0,2 мм, ωmin – циклическая частота при t0=5 мм
Из графика (рис. 2) можно сделать вывод, что статическая жесткость с влияет на частоту в большей степени, чем добавка ![]() (см. уравнение (5)), представляющая собой динамическую «жесткость» и включающая в себя глубину резания.
(см. уравнение (5)), представляющая собой динамическую «жесткость» и включающая в себя глубину резания.
Математическая модель колебательной системы
При построении математической модели были приняты следующие допущения:
- динамическая система состоит из двух приведенных масс – резца и заготовки;
- резец и заготовка имеют по 3 степени свободы (резец может перемещаться вдоль осей x, y и z, заготовка – перемещаться вдоль осей y и z и вращаться вокруг своей оси);
- в системе отсутствуют случайные возмущения.
Резец и заготовка совершают малые колебательные перемещения (рис. 3).
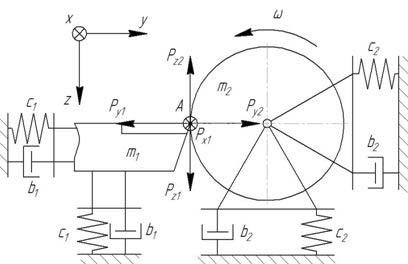
Рисунок 3 – Общая схема колебательной системы при точении (степени свободы, соответствующие осевым колебаниям резца и крутильным колебаниям заготовки, не показаны)
Эти перемещения и их скорости определяют мгновенные режимы резания, отклоняя их значения от номинальных (рис. 4).
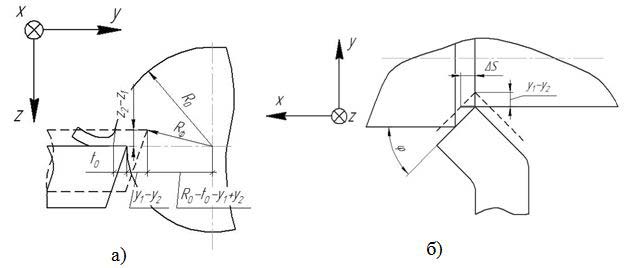
Рисунок 4 – Схемы определения мгновенных значений глубины, скорости резания (а) и подачи (б)
Исходя из приведенных выше схем, были выведены зависимости мгновенных режимов резания от малых перемещений и их скоростей:
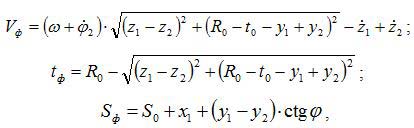
где ω – угловая скорость вращения заготовки; t0, S0 – номинальные значения глубины резания и подачи; Vф, tф, Sф – фактические значения скорости, глубины резания и подачи; R0 - номинальное значение радиуса заготовки.
Найденные зависимости были подставлены в эмпирические формулы для определения составляющих сил резания. Исходя из этого, была составлена система уравнений, описывающая колебания при точении:
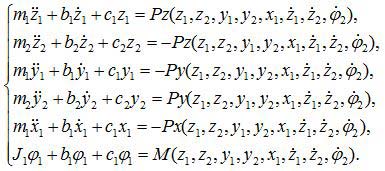
где m, b, c – приведенная масса, коэффициент диссипации и коэффициент жесткости резца (1) и заготовки (2); Px, Py, Pz – осевая, радиальная и тангенциальная составляющие усилия резания; M=Mд-Py(z2-z1)-PzRф – крутящий момент; Mд - крутящий момент на двигателе; Rф - фактический радиус детали.
Система уравнений решалась численно центрированным методом Эйлера с шагом интегрирования 10-5. Полученные результаты сравнивались с опытными данными, приведенными в работах Г.А. Манжоса [3], А.И. Каширина [1], И.С. Амосова [2], по нескольким критериям. Для краткости изложения приведем сравнение только по двум из них.
Согласно результатам экспериментов, сила резания при отталкивании резца от заготовки больше, чем при врезании. А значит, сила резания не определяется однозначно относительным положением резца и заготовки. Этот же результат получен нами теоретически (рис. 5).
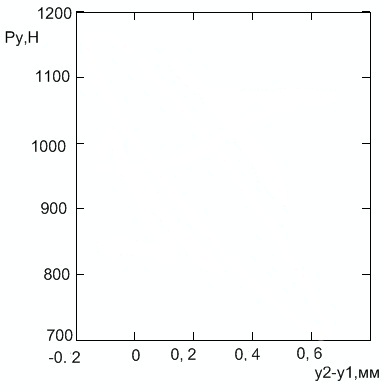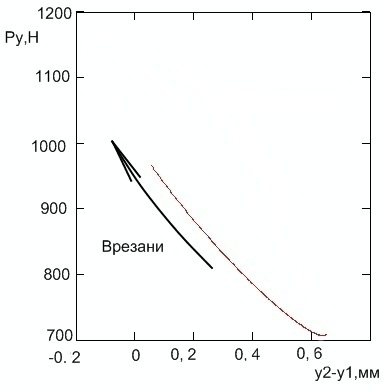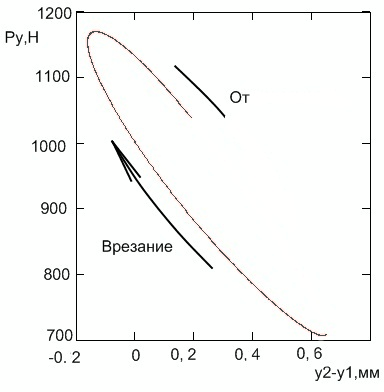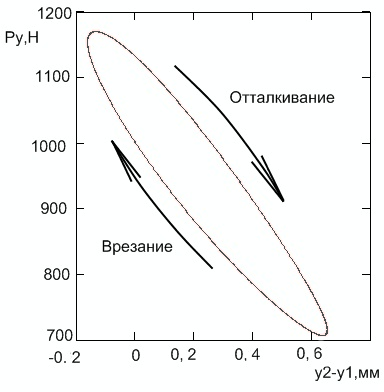
Рисунок 5 – Зависимость радиальной силы от относительных радиальных перемещений резца и заготовки
Кроме того, согласно опытным данным, максимум силы Pz при резании совпадает с максимумом силы Py, т.е. радиальная и тангенциальная силы изменяются синфазно, что также следует из разработанной нами теоретической модели (рис. 6).
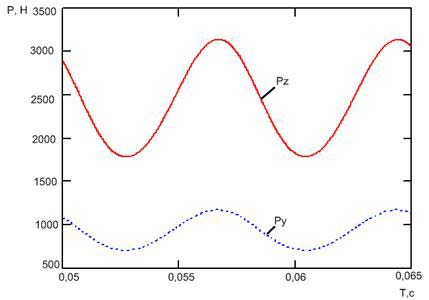
Рисунок 6 – График, иллюстрирующий синфазность радиальной и тангенциальной составляющих силы резания
Из вышеизложенного можно сделать вывод, что разработанная математическая модель не противоречит результатам экспериментов по следующим критериям:
- радиальная сила при врезании больше, чем при отталкивании, т.е. не определяется однозначно относительными радиальными перемещениями резца и заготовки;
- радиальная и тангенциальная силы в процессе резания изменяются синфазно.
Предварительные выводы
Из всего вышесказанного можно сделать вывод, что созданная математическая модель достаточно точно описывает динамическую систему точения, поскольку полученные теоретические результаты не противоречат практическим данным других авторов. Она подтверждает предположение о том, что вибрации при резании металла не являются вынужденными (кроме случаев, когда присутствует внешняя вынуждающая сила), а представляют собой процесс, обусловленный самим резанием. То есть вибрации при резании являются автоколебаниями.
Список использованной литературы
- Каширин А. И. Исследование вибраций при резании металла. – М.: Академия наук СССР, 1944. – 131 с.
- Амосов И. С. Осциллографическое исследование вибраций при резании металлов. – М.: Машгиз, 1951. – 64 с.
- Манжос Г. А. Исследование вибраций в условиях скоростного точения и изыскание методов борьбы с ними. – М.: Машгиз, 1951. – 47 с.
- Соколовский А. П. Научные основы технологии машиностроения / А. П. Соколовский. - М.: Машгиз, 1955. - 516 с.
- Ильницкий И. И. Колебания в металлорежущих станках и пути их устранения. М.: Машгиз, 1958. – 141 с.
- Жарков И. Г. Вибрации при обработке лезвийным инструментом / И. Г. Жарков. – Л.: Машиностроение, 1986. – 184 с.
- Справочник технолога-машиностроителя. В 2-х т. Т.2 / Под ред. А.Г. Косиловой и Р.К. Мещерякова.- 4-е изд., перераб. и доп. – М.: Машиностроение, 1985. 496 с.
