Реферат
за темою випускної роботи
Зміст:
- Мета роботи
- Ідея роботы
- Актуальність теми
- Короткий літературний огляд
- Вплив глибини різання на частоту коливань
- Математична модель коливальної системи
- Попередні висновки
- Список використаної літератури
ПРИМІТКА: Даний автореферат складено 14.05.2012, тобто до закінчення магістерської роботи. Орієнтовна дата завершення - 15.12.2012.
Мета роботи
Метою даної роботи була розробка комплексної математичної моделі вібрацій при точінні, і порівняння отриманих результатів з експериментальними даними інших авторів для підтвердження зроблених висновків.
Ідея роботи
Ідеєю, покладеної в основу математичної моделі, було наступне припущення. В процесі точіння миттєві значення режимів різання змінюються у зв'язку з коливаннями, що викликає змінність сили різання. На цій підставі стан динамічної системи в кожен момент часу вважаємо однозначно залежать від миттєвих режимів через силу різання.
Актуальність теми роботи
Останнім часом в машинобудуванні спостерігається тенденція до високошвидкісної обробці, що дозволяє заощадити головний невідновлювальний ресурс - час. Основною причиною, що обмежує режими різання, є вібрації, що виникають при будь-якій обробці різанням, в тому числі і при точінні. Тому вишукування причин появи коливань і шляхів боротьби з ними є пріоритетними завданнями сучасності.
При точінні виникають коливання, що впливають на параметри якості і точність одержуваних розмірів. Математичний опис цього процесу дає можливість прогнозувати такі режими різання, які дозволили б уникнути несприятливих динамічних умов.
Короткий літературний огляд
Незважаючи на те, що явища вібрацій в машинах присвячено досить велику кількість робіт, вібрації при різанні металів і причини їх появи досліджені вкрай слабо.
Розвиток поглядів на причину появи вібрацій при точінні починалося з дослідів Нікольсона. Він проводив досліди по обточуванню зовнішньої циліндричної поверхні на токарних верстатах при дуже малих швидкостях різання (близько 1,13 мм / хв). Згідно з отриманими в результаті даними, зусилля різання завдяки освіті і послідовному сколюванню елементів стружки є змінною періодичної силою, яка може викликати ритмічні коливання. На підставі, цих дослідів зусилля різання багатьма авторами протягом ряду років трактувалося як періодично змінюється сила, що має максимум в момент найбільшої деформації елемента стружки і мінімум в момент сколювання елемента.[1]
Таким чином з'явилося уявлення про вібраціях при різанні металів, як про вимушені під дією періодично змінюється зусилля різання. Неспроможність такого подання про вібраціях при різанні металів легко бачити з наступного:
- Немає жодних підстав екстраполювати результати дослідів Нікольсона, проведених при надзвичайно малих швидкостях різання, на практично застосовуються (в 20000-100000 разів більші) швидкості різання. Як відомо, при дуже малих швидкостях, різання навіть м'які сталі можуть давати елементну стружку.
- Якби викладене пояснення природи вібрацій при різанні було справедливо, то, природно, при всякій обробці металів різанням мало б місце освіта елементної стружки і поява вібрацій, однак це ні в якій мірі не підтверджується практикою.
- Відомо, що практично крихкі метали, наприклад чавун і т. п., дають при обробці різко виражену елементну стружку; в той же час такі метали зазвичай не схильні до появи вібрацій, тоді як в'язкі сталі, що дають зазвичай зливну стружку, особливо часто викликають сильні вібрації при практично застосовуваних швидкостях різання.[1]
Існує ще інше пояснення вібрацій при різанні металів, а саме, що ці вібрації представляють собою резонансні коливання внаслідок збігу частот - періодичних коливанні зусиль різання (під впливом освіти і сколювання елементів стружки) і вільних коливань якого з вузлів верстата.
Тейлор так формулює це пояснення: „Коли ці періоди найбільшого і найменшого тиску синхронні або приблизно збігаються з природними коливаннями оброблюваного предмета або різця, або супорта, або який-небудь іншій частині верстата, то при роботі з'являється тремтіння”.
Таке пояснення явищу вібрацій дається і японським дослідником Сідзоу Дої: „При тремтінні число змін сили синхронно з числом власних коливань однієї частини токарного верстата і породжує резонанс.”.
Згідно дослідам Тейлора, причиною є збіг частот змін сили різання з власною частотою коливань якого вузла верстата або заготовки.
Після докази неправомірності цих точок зору причиною вібрацій стали називати механізм процесу різання, тобто мають місце автоколивання (Манжос, Амосов, Соколовський та ін.). [1, 2, 3, 4].
І.С. Амосов досліджував коливання оброблюваної деталі та інструменту в горизонтальному і вертикальному напрямках і зміна горизонтальної та вертикальної складових сили різання за часом. Деталь коливається з більшою амплітудою, ніж інструмент; деталь і інструмент роблять коливання в двох основних напрямках з певним зрушенням по фазі, внаслідок чого їх рух виражається у вигляді замкнутої кривої. У результаті вимірів коливань і сили побудована залежність „сила-шлях”. Різниця отриманих площ на графіку цієї залежності висловлює роботу, повідомлену коливальної системі. [2]
Г.А. Манжос встановила, що, при різанні виникають автоколивання. Вимірювання профілю хвиль на обробленій поверхні показало, що хвилі не мають синусоїдальну форму. На підставі цього був зроблений висновок, що виникають автоколивання носять різко виражений нелінійний характер.[3]
І.І. Ільницький зробив висновок, що зміна дійсного переднього кута в процесі різання збуджує коливальні процеси, викликаючи змінну силу для їх підтримки. Періодичне зміна заднього кута викликає змінну силу тертя, яка підтримує коливання в технологічній системі СНІД. На відміну від інших дослідників він вважав, що ця змінна сила виникає не тільки після утворення хвилястості, а негайно в результаті обурення системи. [5]
А.І. Каширін встановив три причини, які підтримують автоколивання при різанні сталей: перша з них обумовлена силою тертя між стружкою і передньою поверхнею і між оброблюваною деталлю і задньою поверхнею, друга - змінними силами через зміну робочих кутів різання в процесі коливального руху; третя, названа ним вторинним обуренням, - змінним перетином зрізу, що виникають при русі різця по вібраційному сліду від попереднього проходу.[1]
А.П. Соколовський показав, що частина сили різання ΔPy являє собою функцію швидкості відносних коливань між інструментом і оброблюваною деталлю. Він пояснює це тим, що величина сили різання при русі різця в сторону деталі відрізняється від сили, що утворюється при русі різця в зворотному напрямку. Інструмент врізається в матеріал з меншою силою, ніж при виході з матеріалу, так як різець зрізає матеріал, попередньо випробував пластичну деформацію і тому зміцнений. Тому А.П. Соколовський приймає, що значення ΔPy залежить від ставлення швидкості коливань до швидкості різання. [4]
Вплив глибини різання на частоту коливань
Щоб проаналізувати вплив глибини різання на частоту коливань при різанні, розглянемо ідеалізовану схему точіння циліндричної заготовки (рис. 1), що здійснює коливання в радіальному напрямку.
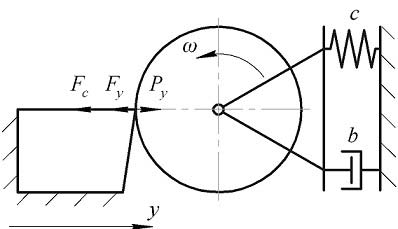
Рисунок 1 – Схема динамічної системи різання з одним ступенем свободи в радіальному напрямку
Зобразимо заготовку наведеної масою m, а дію жорстко закріпленого різця - радіальною силою Py, обумовлює радіальні коливання заготовки, коефіцієнт статичної жорсткості якої позначимо с. Демпфер зображує втрати енергії з коефіцієнтом в'язкого тертя (дисипації) b. Радіальної силі протидіють відновлююча сила Fy і сила опору Fc, які представимо прямо пропорційними переміщенню і швидкості коливань відповідно:
Тоді рівняння руху буде мати наступний вигляд:
Складову сили різання Pyзапишемо у вигляді [7]:
(1) |
і представимо її залежною від радіальних коливань.
Щоб розглянути вплив миттєвої глибини різання на частоту коливань при обробці, будемо вважати глибину змінної, а всі інші величини постійними, об'єднавши їх в коефіцієнт, K, який, згідно (1), запишемо у вигляді:
де Cp, Kp, n, p, x - емпіричні коефіцієнти [7].
Тоді сила різання представляється так:де t - миттєва глибина різання.
Миттєву глибину різання можна представити сумою постійної (номінальної глибини) і змінної частин, тобто власне радіальних коливань заготовки, описуваних функцією y:
де t0 - номінальна глибина різання.
Рівняння руху набуде вигляду:
(2) |
Знехтуємо в першому наближенні втратами енергії, вважаючи b=0, і розкладемо праву частину рівняння (2) в ряд Маклорена до лінійного члена. В результаті отримаємо:
(3) |
Функцію yзапишемо у вигляді:
де y1 - центровані коливання, y2 - відведення коливань.
Визначимо відведення коливань з формули (3), переписавши її у вигляді:
Прирівнявши коефіцієнти при y1 та y2, одержимо систему двох рівнянь:
 |
(4) |
З другого рівняння системи (4) визначимо відведення коливань:
З першого рівняння системи (4) знайдемо частоту коливань:
 |
(5) |
Задамося наступними вихідними даними: приведена маса заготовки m=18 кг, матеріал заготовки - сталь 40Х, матеріал ріжучої частини інструменту - Т5К10, виліт заготовки 300 мм, діаметр заготовки 100 мм, геометричні параметри різця: α=3°, γ=9°, β=78°, φ=φ1=45°, ε=90°, λ=0°, розміри державки різця 16×25 мм, радіус заокруглення при вершині r=2 мм, стан поверхні заготовки - без кірки, Ra 6,3 мкм, стійкість інструменту Т=45 хв. Визначимо частоту вібрацій заготовки за формулою (5) при різних значеннях глибини різання (від 0,2 мм до 5 мм з кроком 0,2 мм) і коефіцієнта статичної жорсткості деталі. Результати обчислень зведемо в таблицю 1 (з кроком глибини різання 1 мм) і побудуємо графік (рис. 2).
Глибина різання t0, мм |
Циклічна частота ω, рад/с, при коефіцієнті жорсткості с, Н/м: |
|||
|---|---|---|---|---|
105 |
106 |
107 |
108 |
|
1 |
200 |
298 |
761 |
2341 |
2 |
194 |
294 |
759 |
2340 |
3 |
191 |
292 |
758 |
2340 |
4 |
188 |
291 |
758 |
2340 |
5 |
186 |
289 |
757 |
2339 |
З проведених розрахунків можна зробити висновок, що зі збільшенням статичної жорсткості заготовки вплив глибини різання на циклічну частоту радіальних коливань заготовки зменшується. Наприклад, при c=105 H/м зміна частоти складає 15%, а при c=108 - 0,1%. З цього можна зробити висновок, що глибина різання майже не впливає на циклічну частоту коливань. Отримані результати не суперечать досвідченим даними [1,4,5].
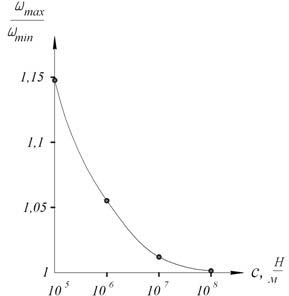
Рисунок 2 – Залежність зміни циклічної частоти від жорсткості деталі: ωmax – циклічна частота при t0=0,2 мм, ωmin – циклічна частота при t0=5 мм
З графіка (рис. 2) можна зробити висновок, що статична жорсткість с впливає на частоту в більшій мірі, ніж додаток ![]() (див. рівняння (5)), що представляє собою динамічну „жорсткість” і включає в себе глибину різання.
(див. рівняння (5)), що представляє собою динамічну „жорсткість” і включає в себе глибину різання.
Математична модель коливальної системи
При побудові математичної моделі були прийняті наступні допущення:
- динамічна система складається з двох наведених мас - різця і заготовки;
- різець і заготівля мають по 3 ступеня свободи (різець може переміщатися уздовж осей x, y и z, заготовка - переміщатися уздовж осей y та z і обертатися навколо своєї осі);
- в системі відсутні випадкові обурення.
Різець і заготовка роблять малі коливальні переміщення (рис. 3).
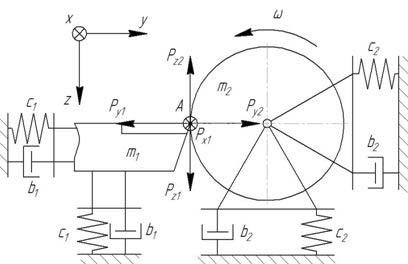
Рисунок 3 – Загальна схема коливальної системи при точінні (ступеня свободи, відповідні осьовим коливань різця і крутильним коливань заготовки, не показані)
Ці переміщення та їх швидкості визначають миттєві режими різання, відхиляючи їх значення від номінальних (рис. 4).
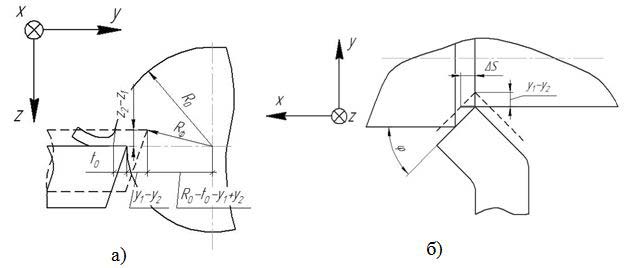
Рисунок 4 – Схеми визначення миттєвих значень глибини, швидкості різання (а) і подачі (б)
Виходячи з наведених вище схем, були виведені залежності миттєвих режимів різання від малих переміщень та їх швидкостей:
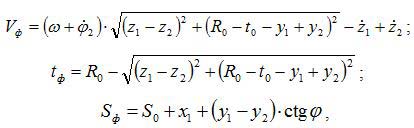
де ω – кутова швидкість обертання заготовки; t0, S0 – номінальні значення глибини різання і подачі; Vф, tф, Sф – фактичні значення швидкості, глибини різання і подачі; R0 - номінальне значення радіуса заготовки.
Знайдені залежності були підставлені в емпіричні формули для визначення складових сил різання. Виходячи з цього, була складена система рівнянь, що описує коливання при точінні:
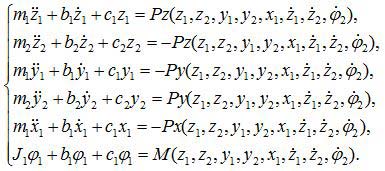
де m, b, c – приведена маса, коефіцієнт дисипації і коефіцієнт жорсткості різця (1) і заготівки (2); Px, Py, Pz – осьова, радіальна та тангенціальна складові зусилля різання; M=Mд-Py(z2-z1)-PzRф – крутний момент; Mд – крутний момент на двигуні; Rф - фактичний радіус деталі.
Система рівнянь вирішувалася чисельно центрованим методом Ейлера з кроком інтегрування 10-5. Отримані результати порівнювалися з досвідченими даними, наведеними в роботах Г.А. Манжоса [3], А.Ш. Каширіна [1], І.С. Амосова [2], за кількома критеріями. Для стислості викладу наведемо порівняння тільки по двох з них.
Згідно з результатами експериментів, сила різання при відштовхуванні різця від заготівлі більше, ніж при врізання. А значить, сила різання не визначається однозначно відносним становищем різця і заготовки. Цей же результат отримано нами теоретично (рис. 5).
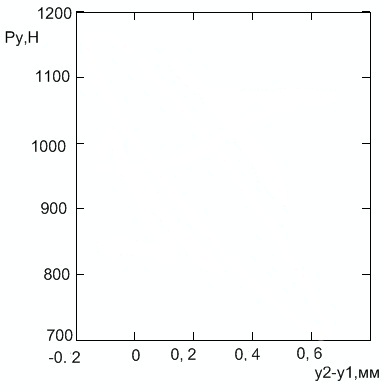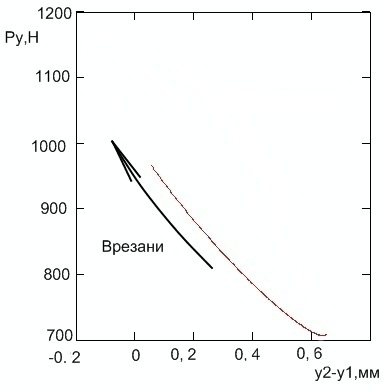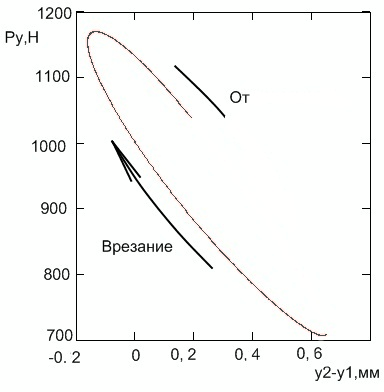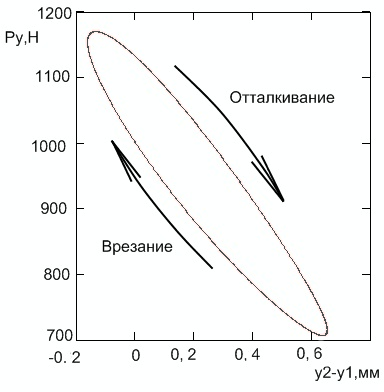
Рисунок 5 – Залежність радіальної сили від відносних радіальних переміщень різця і заготовки
Крім того, згідно досвідченим даними, максимум сили Pz при різанні збігається з максимумом сили Py, тобто радіальна і тангенціальна сили змінюються синфазно, що також випливає з розробленої нами теоретичної моделі (рис. 6).
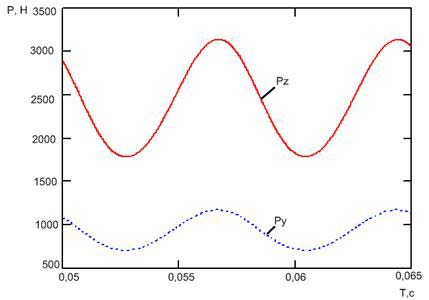
Рисунок 6 – Графік, що ілюструє синфазність радіальної і тангенціальною складових сили різання
З вищевикладеного можна зробити висновок, що розроблена математична модель не суперечить результатам експериментів за наступними критеріями:
- радіальна сила при врізання більше, ніж при відштовхуванні, тобто не визначається однозначно відносними радіальними переміщеннями різця і заготовки;
- радіальна і тангенціальна сили в процесі різання змінюються синфазно.
Попередні висновки
З усього вищесказаного можна зробити висновок, що створена математична модель досить точно описує динамічну систему точіння, оскільки отримані теоретичні результати не суперечать практичним даними інших авторів. Вона підтверджує припущення про те, що вібрації при різанні металу не є вимушеними (крім випадків, коли присутня зовнішня змушує сила), а являють собою процес, обумовлений самим різанням. Тобто вібрації при різанні є автоколиваннями.
Список використаної літератури:
- Каширин А. И. Исследование вибраций при резании металла. – М.: Академия наук СССР, 1944. – 131 с.
- Амосов И. С. Осциллографическое исследование вибраций при резании металлов. – М.: Машгиз, 1951. – 64 с.
- Манжос Г. А. Исследование вибраций в условиях скоростного точения и изыскание методов борьбы с ними. – М.: Машгиз, 1951. – 47 с.
- Соколовский А. П. Научные основы технологии машиностроения / А. П. Соколовский. – М.: Машгиз, 1955. – 516 с.
- Ильницкий И. И. Колебания в металлорежущих станках и пути их устранения. М.: Машгиз, 1958. – 141 с.
- Жарков И. Г. Вибрации при обработке лезвийным инструментом / И. Г. Жарков. – Л.: Машиностроение, 1986. – 184 с.
- Справочник технолога-машиностроителя. В 2-х т. Т.2 / Под ред. А.Г. Косиловой и Р.К. Мещерякова.– 4-е изд., перераб. и доп. – М.: Машиностроение, 1985. 496 с.
